山东省聊城市莘县2015-2016学年七年级(下)期末数学试卷(解析版)
文档属性
| 名称 | 山东省聊城市莘县2015-2016学年七年级(下)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 114.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-28 12:30:41 | ||
图片预览




文档简介
2015-2016学年山东省聊城市莘县七年级(下)期末数学试卷
一、选择题(每小题3分,共36分)
1.下面四个图形中,∠1与∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个
2.下列计算中,正确的是( )
A.x3÷x=x2
B.a6÷a2=a3
C.xx3=x3
D.x3+x3=x6
3.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4
B.∠1=∠5
C.∠1+∠4=180°
D.∠3=∠5
4.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )
A.4cm
B.5cm
C.小于3cm
D.不大于3cm
5.下列正多边形中,与正三角形同时使用能进行镶嵌的是( )
A.正十二边形
B.正十边形
C.正八边形
D.正五边形
6.若4x2+axy+25y2是一个完全平方式,则a=( )
A.20
B.﹣20
C.±20
D.±10
7.若x+y=7,xy=﹣11,则x2+y2的值是( )
A.49
B.27
C.38
D.71
8.如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
A.60°
B.25°
C.35°
D.45°
9.如图,l1∥l2,则α=( )
A.50°
B.60°
C.70°
D.80°
10.已知是二元一次方程组的解,则a﹣b的值为( )
A.﹣1
B.1
C.2
D.3
11.利用图形中面积的等量关系可以得到某
( http: / / www.21cnjy.com )些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
A.=a2﹣b2
B.=a2+ab
D.a(a﹣b)=a2﹣ab
12.玩具车间每天能生产甲种玩具零件24个
( http: / / www.21cnjy.com )或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有( )
A.
B.
C.
D.
二、填空题(每小题3分,计15分)
13.把0.0000123用科学记数法表示为 .
14.已知点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,则点P的坐标是 .
15.如果等腰三角形的一个外角为80°,那么它的底角为 度.
16.若(am+1bn+2)(a2n﹣1b2n)=a5b3,则m+n的值为 .
17.(x2﹣mx+3)(3x﹣2)的积中不含x的二次项,则m的值是 .
三、解答题(共计69分)
18.计算:
(1)﹣(﹣)﹣2+(π﹣3.14)0
(2)(2x+3y)2﹣(2x+y)(2x﹣y)
19.先化简,再求值:(3a+1)(2a﹣3)﹣(6a﹣5)(a﹣4),其中a=2.
20.分解因式:
(1)81x4﹣16y4
(2)y2+y+.
21.解方程组
(1)
(2).
22.已知(a+b)2=5,(a﹣b)2=2,求下列各式的值:
(1)ab
(2)a2+b2.
23.如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
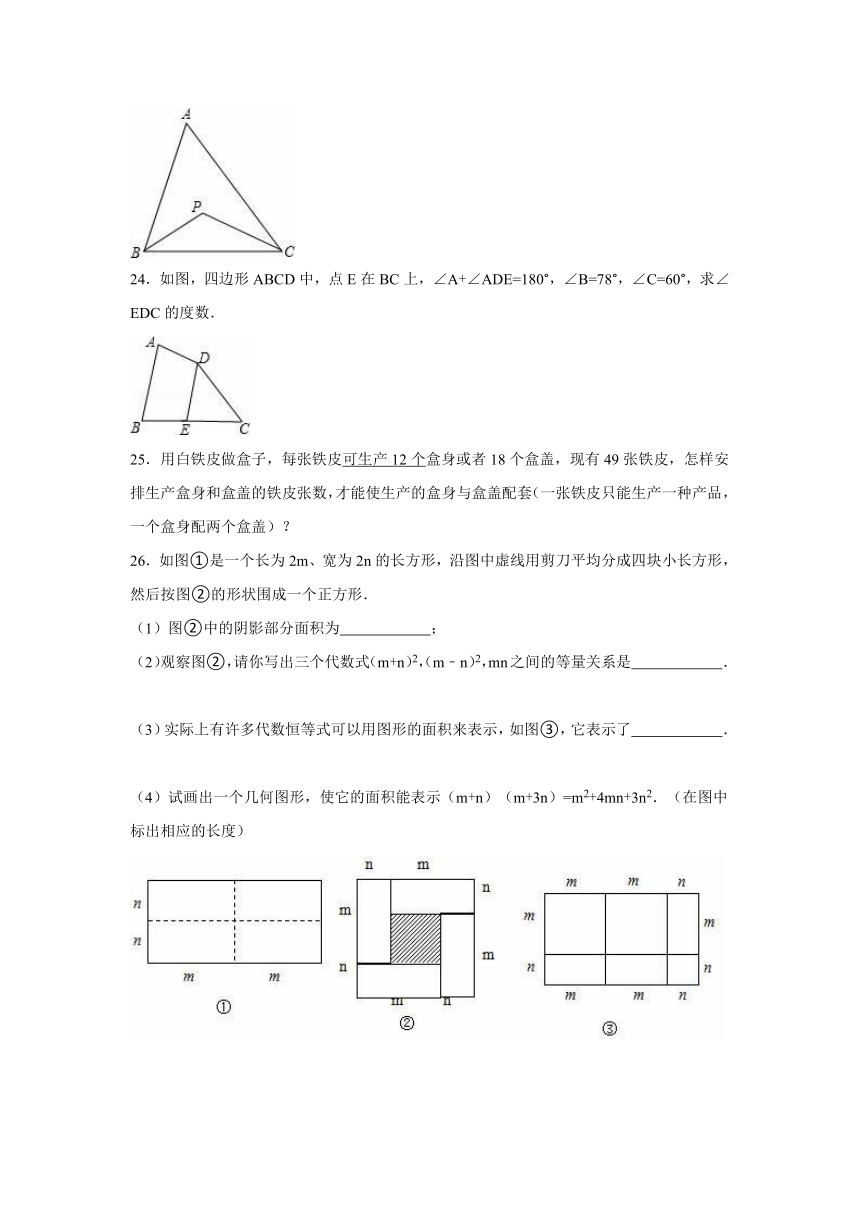
24.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
25.用白铁皮做盒子,每张铁皮可生产12个
( http: / / www.21cnjy.com )盒身或者18个盒盖,现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才能使生产的盒身与盒盖配套(一张铁皮只能生产一种产品,一个盒身配两个盒盖)?
26.如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 ;
(2)观察图②,请你写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 .
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
2015-2016学年山东省聊城市莘县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共36分)
1.下面四个图形中,∠1与∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个
【考点】对顶角、邻补角.
【分析】根据对顶角的定义,两条直线相交后所得的只有一个公共顶点且两边互为反向延长线,这样的两个角叫做对顶角,即可解答.
【解答】解:根据对顶角的定义可知:只有第3个图中的是对顶角,其它都不是.
故选:A.
【点评】本题考查对顶角的定义,解决本题的关键是熟记对顶角的定义.
2.下列计算中,正确的是( )
A.x3÷x=x2
B.a6÷a2=a3
C.xx3=x3
D.x3+x3=x6
【考点】同底数幂的除法;合并同类项;同底数幂的乘法.
【分析】根据合并同类项的法则,同底数幂的乘法与除法的知识求解即可求得答案.
【解答】解:A、x3÷x=x2,故A选项正确;
B、a6÷a2=a4,故B选项错误;
C、xx3=x4,故C选项错误;
D、x3+x3=2x3,故D选项错误.
故选:A.
【点评】此题考查了合并同类项的法则,同底数幂的乘法与除法等知识,解题要注意细心.
3.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4
B.∠1=∠5
C.∠1+∠4=180°
D.∠3=∠5
【考点】平行线的判定.
【分析】由平行线的判定定理易知A、B都能判定AB∥CD;
选项C中可得出∠1=∠5,从而判定AB∥CD;
选项D中同旁内角相等,但不一定互补,所以不能判定AB∥CD.
【解答】解:∠3=∠5是同旁内角相等,但不一定互补,所以不能判定AB∥CD.
故选D.
【点评】正确识别“三线八角
( http: / / www.21cnjy.com )”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
4.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )
A.4cm
B.5cm
C.小于3cm
D.不大于3cm
【考点】点到直线的距离.
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线a的距离≤PC,
即点P到直线a的距离不大于3cm.
故选;D.
【点评】本题主要考查了垂线段最短的性质,熟记性质是解题的关键.
5.下列正多边形中,与正三角形同时使用能进行镶嵌的是( )
A.正十二边形
B.正十边形
C.正八边形
D.正五边形
【考点】平面镶嵌(密铺).
【分析】分别求出各个正多边形的每个内角的度数,结合密铺的条件即可求出答案.
【解答】解:正三角形的每个内角是60°,
A、正十二边形每个内角是180°﹣36
( http: / / www.21cnjy.com )0°÷12=150°,∵60°+2×150°=360°,∴与正三角形同时使用,能进行密铺,故本选项正确;
B、正十边形的每个内角180°﹣360°÷10=144°,显然不能构成360°的周角,故本选项错误;
C、正八边形的每个内角180°﹣360°÷8=135°,显然不能构成360°的周角,故本选项错误;
D、正八边形的每个内角180°﹣360°÷5=108°,显然不能构成360°的周角,故本选项错误.
故选A.
【点评】本题考查平面密铺的知识,几
( http: / / www.21cnjy.com )何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°﹣360°÷边数.
6.若4x2+axy+25y2是一个完全平方式,则a=( )
A.20
B.﹣20
C.±20
D.±10
【考点】完全平方式.
【分析】根据这里首末两项是2x和5y这两个数的平方,那么中间一项为加上或减去2x和5y乘积的2倍,即可得出a的值.
【解答】解:∵4x2+axy+25y2是一个完全平方式,
∴(2x±5y)2=4x2±20xy+25y2,
∴a=±20,
故选:C.
【点评】此题主要考查了完全平方公式
( http: / / www.21cnjy.com )的应用;两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
7.若x+y=7,xy=﹣11,则x2+y2的值是( )
A.49
B.27
C.38
D.71
【考点】完全平方公式.
【分析】把x+y=7两边平方利用完全平方公式展开,然后把xy=﹣11代入计算整理即可求解.
【解答】解:∵x+y=7,
∴(x+y)2=49,
即x2+2xy+y2=49,
∵xy=﹣11,
∴x2+y2=49﹣2×(﹣11)=49+22=71.
故选D.
【点评】本题考查了完全平方公式的应用,把已知条件x+y=7两边平方是解题的关键.
8.如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
A.60°
B.25°
C.35°
D.45°
【考点】平行线的性质.
【分析】由已知可以推出∠A的同位角的度数为∠DME=60°,根据三角形外角定理得∠E=35°
【解答】解:∵AB∥CD,∠A=60°,
∴∠DME=∠A=60°,
∴∠E=∠DME﹣∠C=60°﹣25°=35°,
故选C.
【点评】本题主要考查平行线的性质、三角新股内角和定理,关键看出∠A的同位角是三角形的一个外角.
9.如图,l1∥l2,则α=( )
A.50°
B.60°
C.70°
D.80°
【考点】平行线的性质.
【分析】首先过点B作BE∥l1,由l1∥l2
( http: / / www.21cnjy.com ),即可得BE∥l1∥l2,根据两直线平行,同旁内角互补与两直线平行,内错角相等,即可求得∠ABE与∠CBE度数,则可求得角α的度数.
【解答】解:过点B作BE∥l1,
∵l1∥l2,
∴BE∥l1∥l2,
∴∠ABE+∠A=180°,∠CBE=∠C=30°,
∴∠ABE=180°﹣∠A=180°﹣140°=40°,
∴∠α=∠ABE+∠CBE=70°.
故选C.
【点评】此题考查了平行线的性质.解题的关键是注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,以及辅助线的作法.
10.已知是二元一次方程组的解,则a﹣b的值为( )
A.﹣1
B.1
C.2
D.3
【考点】二元一次方程的解.
【分析】根据二元一次方程组的解的定义,将代入原方程组,分别求得a、b的值,然后再来求a﹣b的值.
【解答】解:∵已知是二元一次方程组的解,
∴
由①+②,得a=2,
由①﹣②,得b=3,
∴a﹣b=﹣1;
故选:A.
【点评】此题考查了二元一次方程组的解法.二元一次方程组的解法有两种:代入法和加减法,不管哪种方法,目的都是“消元”.
11.利用图形中面积的等量
( http: / / www.21cnjy.com )关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
A.=a2﹣b2
B.=a2+ab
D.a(a﹣b)=a2﹣ab
【考点】完全平方公式的几何背景.
【分析】根据图形,左上角正方形的面积等于大正方形的面积减去两个矩形的面积,然后加上多减去的右下角的小正方形的面积.
【解答】解:大正方形的面积=(a﹣b)2,
还可以表示为a2﹣2ab+b2,
∴(a﹣b)2=a2﹣2ab+b2.
故选B.
【点评】正确列出正方形面积的两种表示是得出公式的关键,也考查了对完全平方公式的理解能力.
12.玩具车间每天能生产
( http: / / www.21cnjy.com )甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有( )
A.
B.
C.
D.
【考点】由实际问题抽象出二元一次方程组.
【分析】根据每天能生产甲种玩具零件24个或乙种玩具零件12个,则x天能够生产24x个甲种零件,y天能够生产12y个乙种零件.
此题中的等量关系有:
①总天数是60天;
②根据甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,则乙种零件应是甲种零件的2倍,可列方程为2×24x=12y.
【解答】解:根据总天数是60天,可得x+y=60;根据乙种零件应是甲种零件的2倍,可列方程为2×24x=12y.
则可列方程组为.
故选C.
【点评】此题的难点在于列第二个方程,注
( http: / / www.21cnjy.com )意甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,说明生产的乙种零件是甲种零件的2倍,要列方程,则应让少的2倍,方可列出方程.
二、填空题(每小题3分,计15分)
13.把0.0000123用科学记数法表示为 1.23×10﹣5 .
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的正数也可以利用科
( http: / / www.21cnjy.com )学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.0000123=1.23×10﹣5,
故答案为:1.23×10﹣5.
【点评】本题考查用科学记数法表示较
( http: / / www.21cnjy.com )小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
14.已知点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,则点P的坐标是 (3,﹣2) .
【考点】点的坐标.
【分析】根据第四象限内点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
【解答】解:∵点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,
∴点P的横坐标为3,纵坐标为﹣2,
∴点P的坐标是(3,﹣2).
故答案为:(3,﹣2).
【点评】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.
15.如果等腰三角形的一个外角为80°,那么它的底角为 40 度.
【考点】等腰三角形的性质.
【分析】根据三角形的外角性质和等腰三角形的性质求解.
【解答】解:∵等腰三角形的一个外角为80°,
∴相邻角为180°﹣80°=100°,
∵三角形的底角不能为钝角,
∴100°角为顶角,
∴底角为:(180°﹣100°)÷2=40°.
故答案为:40.
【点评】本题考查了等腰三角形的性质,解题的关键是掌握三角形的内角和定理以及等腰三角形的性质.
16.若(am+1bn+2)(a2n﹣1b2n)=a5b3,则m+n的值为 .
【考点】单项式乘单项式.
【分析】已知等式左边利用单项式乘以单项式法则计算,根据单项式相等的条件求出m与n的值,即可求出m+n的值.
【解答】解:已知等式整理得:am+2nb3n+2=a5b3,
可得,
解得:m=,n=,
则m+n=,
故答案为:
【点评】此题考查了单项式乘单项式,熟练掌握运算法则是解本题的关键.
17.(x2﹣mx+3)(3x﹣2)的积中不含x的二次项,则m的值是 ﹣ .
【考点】多项式乘多项式.
【分析】先依据多项式乘多项式法则计算,然后依据x的二次项系数为0求解即可.
【解答】解:原式=3x3﹣3mx2+9x﹣2x2+2mx﹣6
=3x3﹣(3m+2)x2+(2m+9)x﹣6.
∵不含x的二次项,
∴3m+2=0.
∴m=﹣.
故答案为:﹣.
【点评】本题主要考查的是多项式乘多项式法则的应用,依据x的二次项的系数为0列方程求解即可.
三、解答题(共计69分)
18.计算:
(1)﹣(﹣)﹣2+(π﹣3.14)0
(2)(2x+3y)2﹣(2x+y)(2x﹣y)
【考点】平方差公式;完全平方公式;零指数幂;负整数指数幂.
【分析】(1)先根据平方差公式,负整数指数幂,零指数幂分别求出每一部分的值,再合并即可;
(2)先根据完全平方公式和平方差公式展开,再合并同类项即可.
【解答】解:(1)原式=a2﹣b2﹣4+1
=a2﹣b2﹣3;
(2)原式=4x2+12xy+9y2﹣4x2+y2
=12xy+10y2.
【点评】本题考查了完全平方公式,平方差公
( http: / / www.21cnjy.com )式,负整数指数幂,零指数幂的应用,能熟记知识点是解此题的关键,注意:完全平方公式是:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,平方差公式为=a2﹣b2.
19.先化简,再求值:(3a+1)(2a﹣3)﹣(6a﹣5)(a﹣4),其中a=2.
【考点】整式的混合运算—化简求值.
【分析】先算乘法,再合并同类项,最后代入求出即可.
【解答】解:(3a+1)(2a﹣3)﹣(6a﹣5)(a﹣4)
=6a2﹣9a+2a﹣3﹣6a2+24a+5a﹣20
=22a﹣23,
当a=2时,原式=22×2﹣23=21.
【点评】本题考查了整式的混合运算和求值的应用,主要考查学生的化简能力和计算能力.
20.分解因式:
(1)81x4﹣16y4
(2)y2+y+.
【考点】提公因式法与公式法的综合运用.
【分析】(1)两次利用平方差公式分解因式即可;
(2)利用完全平方公式分解因式.
【解答】解:(1)81x4﹣16y4,
=(9x2+4y2)(9x2﹣4y2),
=(9x2+4y2)(3x+2y)(3x﹣2y);
(2)y2+y+=(y+)2.
【点评】本题考查了提公因式法与公式法
( http: / / www.21cnjy.com )分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.
21.解方程组
(1)
(2).
【考点】解二元一次方程组.
【分析】(1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【解答】解:(1),
①×8﹣②得:5x=10,即x=2,
把x=2代入①得:y=﹣1,
则方程组的解为;
(2),
①+②×3得:19x=19,即x=1,
把x=1代入①得:y=2,
则方程组的解为.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
22.已知(a+b)2=5,(a﹣b)2=2,求下列各式的值:
(1)ab
(2)a2+b2.
【考点】完全平方公式.
【分析】根据完全平方公式,即可解答.
【解答】解:(a+b)2=a2+2ab+b2①
(a﹣b)2=a2﹣2ab+b2②
(1)①﹣②得:4ab=5﹣2
∴4ab=3
∴ab=.
(2)①+②得:2a2+2b2=7
∴a2+b2=3.5.
【点评】本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.
23.如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
【考点】三角形内角和定理.
【分析】先根据三角形内角和定理求出∠A
( http: / / www.21cnjy.com )BC+∠ACB的度数,再由角平分线的性质得出∠PBC+∠PCB的度数,由三角形内角和定理即可得出结论.
【解答】解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°﹣60°=120°.
故答案为:120°.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
24.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
【考点】三角形内角和定理;平行线的性质.
【分析】先利用“同旁内角互补,
( http: / / www.21cnjy.com )两直线平行”判定AB∥DE,再利用平行的性质求出∠CED=∠B=78°,再利用三角形内角和求出∠EDC的度数.
【解答】证明:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°.
又∵∠C=60°,
∴∠EDC=180°﹣(∠CED+∠C)
=180°﹣(78°+60°)
=42°.
【点评】主要考查了三角形的内角和定理,三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
同时综合掌握平行的判定以及性质.
25.用白铁皮做盒子,每张铁皮可生产1
( http: / / www.21cnjy.com )2个盒身或者18个盒盖,现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才能使生产的盒身与盒盖配套(一张铁皮只能生产一种产品,一个盒身配两个盒盖)?
【考点】二元一次方程组的应用.
【分析】根据题意可知,本题中的相等关系是(
( http: / / www.21cnjy.com )1)盒身的个数×2=盒盖的个数;(2)制作盒身的铁皮张数+制作盒盖的铁皮张数=49,再列方程组求解.
【解答】解:设用x张铁皮制作盒身,y张铁皮制作盒盖,由题意得
,
解得:.
答:用21张制作盒身,28张制作盒盖,才能使生产的盒身与盒盖配套.
【点评】本题考查了二元一次方
( http: / / www.21cnjy.com )程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.注意运用本题中隐含的一个相等关系:“一个盒身配两个盒盖”.
26.如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 (m+n)2﹣4mn或(m﹣n)2 ;
(2)观察图②,请你写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 (m+n)2﹣4mn=(m﹣n)2 .
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 (2m+n)(m+n)=2m2+3mn+n2 .
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
【考点】完全平方公式的几何背景.
【分析】(1)根据图形表示出阴影部分的面积即可;
(2)根据(1)中的结果得出即可;
(3)根据大长方形面积等于长乘以宽或5个矩形面积和的两种不同算法可列出等式;
(4)画出长m+n和宽m+3n的矩形,再分成8个矩形即可.
【解答】解:(1)图②中阴影部分的面积为(m+n)2﹣4mn或(m﹣n)2,
故答案为:(m+n)2﹣4mn或(m﹣n)2;
(2)三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是(m+n)2﹣4mn=(m﹣n)2,
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)图③表示的关系式为:(2m+n)(m+n)=2m2+3mn+n2,
故答案为:(2m+n)(m+n)=2m2+3mn+n2;
(4)如图所示:.
【点评】本题考查了完全平方公式的几何背景,属于基础题,注意仔细观察图形,表示出各图形的面积是关键.
一、选择题(每小题3分,共36分)
1.下面四个图形中,∠1与∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个
2.下列计算中,正确的是( )
A.x3÷x=x2
B.a6÷a2=a3
C.xx3=x3
D.x3+x3=x6
3.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4
B.∠1=∠5
C.∠1+∠4=180°
D.∠3=∠5
4.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )
A.4cm
B.5cm
C.小于3cm
D.不大于3cm
5.下列正多边形中,与正三角形同时使用能进行镶嵌的是( )
A.正十二边形
B.正十边形
C.正八边形
D.正五边形
6.若4x2+axy+25y2是一个完全平方式,则a=( )
A.20
B.﹣20
C.±20
D.±10
7.若x+y=7,xy=﹣11,则x2+y2的值是( )
A.49
B.27
C.38
D.71
8.如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
A.60°
B.25°
C.35°
D.45°
9.如图,l1∥l2,则α=( )
A.50°
B.60°
C.70°
D.80°
10.已知是二元一次方程组的解,则a﹣b的值为( )
A.﹣1
B.1
C.2
D.3
11.利用图形中面积的等量关系可以得到某
( http: / / www.21cnjy.com )些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
A.=a2﹣b2
B.=a2+ab
D.a(a﹣b)=a2﹣ab
12.玩具车间每天能生产甲种玩具零件24个
( http: / / www.21cnjy.com )或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有( )
A.
B.
C.
D.
二、填空题(每小题3分,计15分)
13.把0.0000123用科学记数法表示为 .
14.已知点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,则点P的坐标是 .
15.如果等腰三角形的一个外角为80°,那么它的底角为 度.
16.若(am+1bn+2)(a2n﹣1b2n)=a5b3,则m+n的值为 .
17.(x2﹣mx+3)(3x﹣2)的积中不含x的二次项,则m的值是 .
三、解答题(共计69分)
18.计算:
(1)﹣(﹣)﹣2+(π﹣3.14)0
(2)(2x+3y)2﹣(2x+y)(2x﹣y)
19.先化简,再求值:(3a+1)(2a﹣3)﹣(6a﹣5)(a﹣4),其中a=2.
20.分解因式:
(1)81x4﹣16y4
(2)y2+y+.
21.解方程组
(1)
(2).
22.已知(a+b)2=5,(a﹣b)2=2,求下列各式的值:
(1)ab
(2)a2+b2.
23.如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
24.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
25.用白铁皮做盒子,每张铁皮可生产12个
( http: / / www.21cnjy.com )盒身或者18个盒盖,现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才能使生产的盒身与盒盖配套(一张铁皮只能生产一种产品,一个盒身配两个盒盖)?
26.如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 ;
(2)观察图②,请你写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 .
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
2015-2016学年山东省聊城市莘县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共36分)
1.下面四个图形中,∠1与∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个
【考点】对顶角、邻补角.
【分析】根据对顶角的定义,两条直线相交后所得的只有一个公共顶点且两边互为反向延长线,这样的两个角叫做对顶角,即可解答.
【解答】解:根据对顶角的定义可知:只有第3个图中的是对顶角,其它都不是.
故选:A.
【点评】本题考查对顶角的定义,解决本题的关键是熟记对顶角的定义.
2.下列计算中,正确的是( )
A.x3÷x=x2
B.a6÷a2=a3
C.xx3=x3
D.x3+x3=x6
【考点】同底数幂的除法;合并同类项;同底数幂的乘法.
【分析】根据合并同类项的法则,同底数幂的乘法与除法的知识求解即可求得答案.
【解答】解:A、x3÷x=x2,故A选项正确;
B、a6÷a2=a4,故B选项错误;
C、xx3=x4,故C选项错误;
D、x3+x3=2x3,故D选项错误.
故选:A.
【点评】此题考查了合并同类项的法则,同底数幂的乘法与除法等知识,解题要注意细心.
3.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4
B.∠1=∠5
C.∠1+∠4=180°
D.∠3=∠5
【考点】平行线的判定.
【分析】由平行线的判定定理易知A、B都能判定AB∥CD;
选项C中可得出∠1=∠5,从而判定AB∥CD;
选项D中同旁内角相等,但不一定互补,所以不能判定AB∥CD.
【解答】解:∠3=∠5是同旁内角相等,但不一定互补,所以不能判定AB∥CD.
故选D.
【点评】正确识别“三线八角
( http: / / www.21cnjy.com )”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
4.点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )
A.4cm
B.5cm
C.小于3cm
D.不大于3cm
【考点】点到直线的距离.
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线a的距离≤PC,
即点P到直线a的距离不大于3cm.
故选;D.
【点评】本题主要考查了垂线段最短的性质,熟记性质是解题的关键.
5.下列正多边形中,与正三角形同时使用能进行镶嵌的是( )
A.正十二边形
B.正十边形
C.正八边形
D.正五边形
【考点】平面镶嵌(密铺).
【分析】分别求出各个正多边形的每个内角的度数,结合密铺的条件即可求出答案.
【解答】解:正三角形的每个内角是60°,
A、正十二边形每个内角是180°﹣36
( http: / / www.21cnjy.com )0°÷12=150°,∵60°+2×150°=360°,∴与正三角形同时使用,能进行密铺,故本选项正确;
B、正十边形的每个内角180°﹣360°÷10=144°,显然不能构成360°的周角,故本选项错误;
C、正八边形的每个内角180°﹣360°÷8=135°,显然不能构成360°的周角,故本选项错误;
D、正八边形的每个内角180°﹣360°÷5=108°,显然不能构成360°的周角,故本选项错误.
故选A.
【点评】本题考查平面密铺的知识,几
( http: / / www.21cnjy.com )何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°﹣360°÷边数.
6.若4x2+axy+25y2是一个完全平方式,则a=( )
A.20
B.﹣20
C.±20
D.±10
【考点】完全平方式.
【分析】根据这里首末两项是2x和5y这两个数的平方,那么中间一项为加上或减去2x和5y乘积的2倍,即可得出a的值.
【解答】解:∵4x2+axy+25y2是一个完全平方式,
∴(2x±5y)2=4x2±20xy+25y2,
∴a=±20,
故选:C.
【点评】此题主要考查了完全平方公式
( http: / / www.21cnjy.com )的应用;两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
7.若x+y=7,xy=﹣11,则x2+y2的值是( )
A.49
B.27
C.38
D.71
【考点】完全平方公式.
【分析】把x+y=7两边平方利用完全平方公式展开,然后把xy=﹣11代入计算整理即可求解.
【解答】解:∵x+y=7,
∴(x+y)2=49,
即x2+2xy+y2=49,
∵xy=﹣11,
∴x2+y2=49﹣2×(﹣11)=49+22=71.
故选D.
【点评】本题考查了完全平方公式的应用,把已知条件x+y=7两边平方是解题的关键.
8.如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
A.60°
B.25°
C.35°
D.45°
【考点】平行线的性质.
【分析】由已知可以推出∠A的同位角的度数为∠DME=60°,根据三角形外角定理得∠E=35°
【解答】解:∵AB∥CD,∠A=60°,
∴∠DME=∠A=60°,
∴∠E=∠DME﹣∠C=60°﹣25°=35°,
故选C.
【点评】本题主要考查平行线的性质、三角新股内角和定理,关键看出∠A的同位角是三角形的一个外角.
9.如图,l1∥l2,则α=( )
A.50°
B.60°
C.70°
D.80°
【考点】平行线的性质.
【分析】首先过点B作BE∥l1,由l1∥l2
( http: / / www.21cnjy.com ),即可得BE∥l1∥l2,根据两直线平行,同旁内角互补与两直线平行,内错角相等,即可求得∠ABE与∠CBE度数,则可求得角α的度数.
【解答】解:过点B作BE∥l1,
∵l1∥l2,
∴BE∥l1∥l2,
∴∠ABE+∠A=180°,∠CBE=∠C=30°,
∴∠ABE=180°﹣∠A=180°﹣140°=40°,
∴∠α=∠ABE+∠CBE=70°.
故选C.
【点评】此题考查了平行线的性质.解题的关键是注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,以及辅助线的作法.
10.已知是二元一次方程组的解,则a﹣b的值为( )
A.﹣1
B.1
C.2
D.3
【考点】二元一次方程的解.
【分析】根据二元一次方程组的解的定义,将代入原方程组,分别求得a、b的值,然后再来求a﹣b的值.
【解答】解:∵已知是二元一次方程组的解,
∴
由①+②,得a=2,
由①﹣②,得b=3,
∴a﹣b=﹣1;
故选:A.
【点评】此题考查了二元一次方程组的解法.二元一次方程组的解法有两种:代入法和加减法,不管哪种方法,目的都是“消元”.
11.利用图形中面积的等量
( http: / / www.21cnjy.com )关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
A.=a2﹣b2
B.=a2+ab
D.a(a﹣b)=a2﹣ab
【考点】完全平方公式的几何背景.
【分析】根据图形,左上角正方形的面积等于大正方形的面积减去两个矩形的面积,然后加上多减去的右下角的小正方形的面积.
【解答】解:大正方形的面积=(a﹣b)2,
还可以表示为a2﹣2ab+b2,
∴(a﹣b)2=a2﹣2ab+b2.
故选B.
【点评】正确列出正方形面积的两种表示是得出公式的关键,也考查了对完全平方公式的理解能力.
12.玩具车间每天能生产
( http: / / www.21cnjy.com )甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有( )
A.
B.
C.
D.
【考点】由实际问题抽象出二元一次方程组.
【分析】根据每天能生产甲种玩具零件24个或乙种玩具零件12个,则x天能够生产24x个甲种零件,y天能够生产12y个乙种零件.
此题中的等量关系有:
①总天数是60天;
②根据甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,则乙种零件应是甲种零件的2倍,可列方程为2×24x=12y.
【解答】解:根据总天数是60天,可得x+y=60;根据乙种零件应是甲种零件的2倍,可列方程为2×24x=12y.
则可列方程组为.
故选C.
【点评】此题的难点在于列第二个方程,注
( http: / / www.21cnjy.com )意甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,说明生产的乙种零件是甲种零件的2倍,要列方程,则应让少的2倍,方可列出方程.
二、填空题(每小题3分,计15分)
13.把0.0000123用科学记数法表示为 1.23×10﹣5 .
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的正数也可以利用科
( http: / / www.21cnjy.com )学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.0000123=1.23×10﹣5,
故答案为:1.23×10﹣5.
【点评】本题考查用科学记数法表示较
( http: / / www.21cnjy.com )小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
14.已知点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,则点P的坐标是 (3,﹣2) .
【考点】点的坐标.
【分析】根据第四象限内点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
【解答】解:∵点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,
∴点P的横坐标为3,纵坐标为﹣2,
∴点P的坐标是(3,﹣2).
故答案为:(3,﹣2).
【点评】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.
15.如果等腰三角形的一个外角为80°,那么它的底角为 40 度.
【考点】等腰三角形的性质.
【分析】根据三角形的外角性质和等腰三角形的性质求解.
【解答】解:∵等腰三角形的一个外角为80°,
∴相邻角为180°﹣80°=100°,
∵三角形的底角不能为钝角,
∴100°角为顶角,
∴底角为:(180°﹣100°)÷2=40°.
故答案为:40.
【点评】本题考查了等腰三角形的性质,解题的关键是掌握三角形的内角和定理以及等腰三角形的性质.
16.若(am+1bn+2)(a2n﹣1b2n)=a5b3,则m+n的值为 .
【考点】单项式乘单项式.
【分析】已知等式左边利用单项式乘以单项式法则计算,根据单项式相等的条件求出m与n的值,即可求出m+n的值.
【解答】解:已知等式整理得:am+2nb3n+2=a5b3,
可得,
解得:m=,n=,
则m+n=,
故答案为:
【点评】此题考查了单项式乘单项式,熟练掌握运算法则是解本题的关键.
17.(x2﹣mx+3)(3x﹣2)的积中不含x的二次项,则m的值是 ﹣ .
【考点】多项式乘多项式.
【分析】先依据多项式乘多项式法则计算,然后依据x的二次项系数为0求解即可.
【解答】解:原式=3x3﹣3mx2+9x﹣2x2+2mx﹣6
=3x3﹣(3m+2)x2+(2m+9)x﹣6.
∵不含x的二次项,
∴3m+2=0.
∴m=﹣.
故答案为:﹣.
【点评】本题主要考查的是多项式乘多项式法则的应用,依据x的二次项的系数为0列方程求解即可.
三、解答题(共计69分)
18.计算:
(1)﹣(﹣)﹣2+(π﹣3.14)0
(2)(2x+3y)2﹣(2x+y)(2x﹣y)
【考点】平方差公式;完全平方公式;零指数幂;负整数指数幂.
【分析】(1)先根据平方差公式,负整数指数幂,零指数幂分别求出每一部分的值,再合并即可;
(2)先根据完全平方公式和平方差公式展开,再合并同类项即可.
【解答】解:(1)原式=a2﹣b2﹣4+1
=a2﹣b2﹣3;
(2)原式=4x2+12xy+9y2﹣4x2+y2
=12xy+10y2.
【点评】本题考查了完全平方公式,平方差公
( http: / / www.21cnjy.com )式,负整数指数幂,零指数幂的应用,能熟记知识点是解此题的关键,注意:完全平方公式是:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,平方差公式为=a2﹣b2.
19.先化简,再求值:(3a+1)(2a﹣3)﹣(6a﹣5)(a﹣4),其中a=2.
【考点】整式的混合运算—化简求值.
【分析】先算乘法,再合并同类项,最后代入求出即可.
【解答】解:(3a+1)(2a﹣3)﹣(6a﹣5)(a﹣4)
=6a2﹣9a+2a﹣3﹣6a2+24a+5a﹣20
=22a﹣23,
当a=2时,原式=22×2﹣23=21.
【点评】本题考查了整式的混合运算和求值的应用,主要考查学生的化简能力和计算能力.
20.分解因式:
(1)81x4﹣16y4
(2)y2+y+.
【考点】提公因式法与公式法的综合运用.
【分析】(1)两次利用平方差公式分解因式即可;
(2)利用完全平方公式分解因式.
【解答】解:(1)81x4﹣16y4,
=(9x2+4y2)(9x2﹣4y2),
=(9x2+4y2)(3x+2y)(3x﹣2y);
(2)y2+y+=(y+)2.
【点评】本题考查了提公因式法与公式法
( http: / / www.21cnjy.com )分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.
21.解方程组
(1)
(2).
【考点】解二元一次方程组.
【分析】(1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【解答】解:(1),
①×8﹣②得:5x=10,即x=2,
把x=2代入①得:y=﹣1,
则方程组的解为;
(2),
①+②×3得:19x=19,即x=1,
把x=1代入①得:y=2,
则方程组的解为.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
22.已知(a+b)2=5,(a﹣b)2=2,求下列各式的值:
(1)ab
(2)a2+b2.
【考点】完全平方公式.
【分析】根据完全平方公式,即可解答.
【解答】解:(a+b)2=a2+2ab+b2①
(a﹣b)2=a2﹣2ab+b2②
(1)①﹣②得:4ab=5﹣2
∴4ab=3
∴ab=.
(2)①+②得:2a2+2b2=7
∴a2+b2=3.5.
【点评】本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.
23.如图,在△ABC中,∠BAC=60°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
【考点】三角形内角和定理.
【分析】先根据三角形内角和定理求出∠A
( http: / / www.21cnjy.com )BC+∠ACB的度数,再由角平分线的性质得出∠PBC+∠PCB的度数,由三角形内角和定理即可得出结论.
【解答】解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°﹣60°=120°.
故答案为:120°.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
24.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
【考点】三角形内角和定理;平行线的性质.
【分析】先利用“同旁内角互补,
( http: / / www.21cnjy.com )两直线平行”判定AB∥DE,再利用平行的性质求出∠CED=∠B=78°,再利用三角形内角和求出∠EDC的度数.
【解答】证明:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°.
又∵∠C=60°,
∴∠EDC=180°﹣(∠CED+∠C)
=180°﹣(78°+60°)
=42°.
【点评】主要考查了三角形的内角和定理,三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
同时综合掌握平行的判定以及性质.
25.用白铁皮做盒子,每张铁皮可生产1
( http: / / www.21cnjy.com )2个盒身或者18个盒盖,现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才能使生产的盒身与盒盖配套(一张铁皮只能生产一种产品,一个盒身配两个盒盖)?
【考点】二元一次方程组的应用.
【分析】根据题意可知,本题中的相等关系是(
( http: / / www.21cnjy.com )1)盒身的个数×2=盒盖的个数;(2)制作盒身的铁皮张数+制作盒盖的铁皮张数=49,再列方程组求解.
【解答】解:设用x张铁皮制作盒身,y张铁皮制作盒盖,由题意得
,
解得:.
答:用21张制作盒身,28张制作盒盖,才能使生产的盒身与盒盖配套.
【点评】本题考查了二元一次方
( http: / / www.21cnjy.com )程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.注意运用本题中隐含的一个相等关系:“一个盒身配两个盒盖”.
26.如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 (m+n)2﹣4mn或(m﹣n)2 ;
(2)观察图②,请你写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 (m+n)2﹣4mn=(m﹣n)2 .
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 (2m+n)(m+n)=2m2+3mn+n2 .
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
【考点】完全平方公式的几何背景.
【分析】(1)根据图形表示出阴影部分的面积即可;
(2)根据(1)中的结果得出即可;
(3)根据大长方形面积等于长乘以宽或5个矩形面积和的两种不同算法可列出等式;
(4)画出长m+n和宽m+3n的矩形,再分成8个矩形即可.
【解答】解:(1)图②中阴影部分的面积为(m+n)2﹣4mn或(m﹣n)2,
故答案为:(m+n)2﹣4mn或(m﹣n)2;
(2)三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是(m+n)2﹣4mn=(m﹣n)2,
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)图③表示的关系式为:(2m+n)(m+n)=2m2+3mn+n2,
故答案为:(2m+n)(m+n)=2m2+3mn+n2;
(4)如图所示:.
【点评】本题考查了完全平方公式的几何背景,属于基础题,注意仔细观察图形,表示出各图形的面积是关键.
同课章节目录
