机车的两种启动过程的分析
图片预览
文档简介
机车的两种启动过程的分析
机车以恒定的功率启动
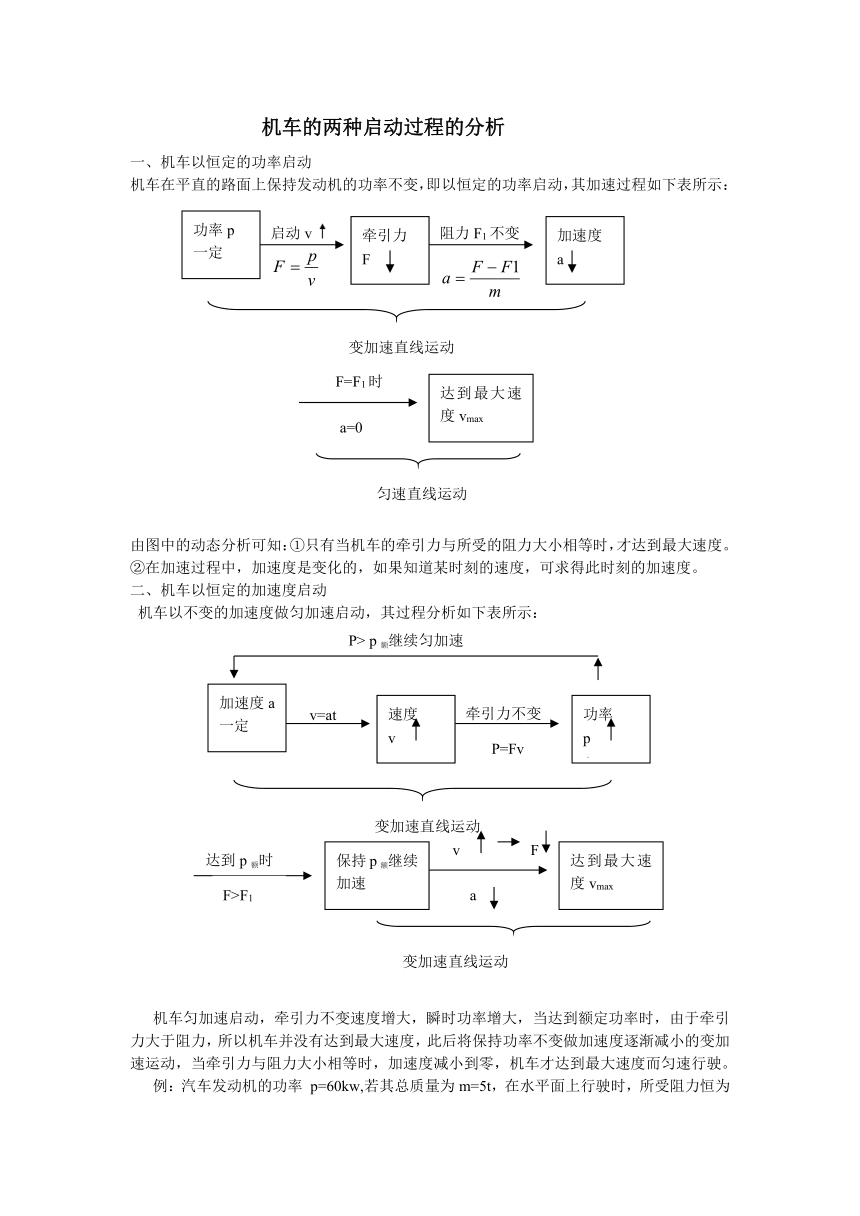
机车在平直的路面上保持发动机的功率不变,即以恒定的功率启动,其加速过程如下表所示:
由图中的动态分析可知:①只有当机车的牵引力与所受的阻力大小相等时,才达到最大速度。
②在加速过程中,加速度是变化的,如果知道某时刻的速度,可求得此时刻的加速度。
机车以恒定的加速度启动
机车以不变的加速度做匀加速启动,其过程分析如下表所示:
机车匀加速启动,牵引力不变速度增大,瞬时功率增大,当达到额定功率时,由于牵引力大于阻力,所以机车并没有达到最大速度,此后将保持功率不变做加速度逐渐减小的变加速运动,当牵引力与阻力大小相等时,加速度减小到零,机车才达到最大速度而匀速行驶。
例:汽车发动机的功率
p=60kw,若其总质量为m=5t,在水平面上行驶时,所受阻力恒为F=5.0×103N,试求:(1)汽车保持恒定功率启动时:①汽车所能达到的最大速度vmax,
②当汽车加速度为2m/s2时,速度是多大?③当汽车速度是6m/s时加速度是多大?
(2)若汽车以a=0.5m/s2的加速度由静止开始做匀加速运动,这一过程能维持多长时间?
思路分析:汽车在运动中所受的阻力大小为:F=5×103N
(1)汽车保持恒定功率启动时,做加速度逐渐减小的加速运动,当加速度减小到零时,速度达到最大
①当a=0时速度最大,所以,此时汽车的牵引力为F1=F=5×103N
则汽车最大速度
vmax==m/s=12m/s
②当汽车加速度为2m/s2时牵引力为F2,由牛顿第二定律得:
F2-F=ma
F2=F+ma=5×103N+5×103×2
N=1.5×104N
汽车的速度
v==m/s=4m/s
③当汽车速度是6m/s时牵引力为
F3==N=1×104N
由牛顿第二定律得:
F3-F=ma
汽车加速度为a==m/s2=1
m/s2
(2)当汽车以恒定的加速度a=0.5m/s2匀加速运动时,汽车的牵引力为F4,由牛顿第二定律得:
F4-F=ma
F4=F+ma=5×103N+5×103×0.5
N=7.5×103N
汽车匀加速运动时,其功率逐渐增大,当功率增大到等于额定功率时,匀加速运动结束,此时汽车的速度为
vt==m/s=8m/s
则汽车匀加速运动时间为
t==s=16s
规律技巧总结:
(1)无论哪种启动方式,机车所能达到的最大速度均为vmax=
P额为汽车的额定功率,F阻为汽车所受的所有阻力
(2)以恒定功率启动,速度增加,牵引力减小,合外力减小,加速度减小,是变加速运动,加速度与合外力的同时性是解题的关键。
(3)汽车以恒定的加速度启动时,汽车的功率逐渐增大,当功率增大到额定功率时,合外力结束,此时汽车的速度为匀加速运动的末速度,但不是汽车所能达到的最大速度,此后汽车还可以保持功率不变做加速度逐渐减小的加速运动,直大加速度减小到零时速度才达到最大。
功率p
一定
启动v
牵引力
F
阻力F1不变
加速度
a
变加速直线运动
F=F1时
a=0
达到最大速度vmax
匀速直线运动
P>
p额继续匀加速
F
a
达到最大速度vmax
变加速直线运动
达到p额时
F>F1
保持p额继续加速
v
加速度a
一定
v=at
速度
v
牵引力不变
P=Fv
功率
p
变加速直线运动
机车以恒定的功率启动
机车在平直的路面上保持发动机的功率不变,即以恒定的功率启动,其加速过程如下表所示:
由图中的动态分析可知:①只有当机车的牵引力与所受的阻力大小相等时,才达到最大速度。
②在加速过程中,加速度是变化的,如果知道某时刻的速度,可求得此时刻的加速度。
机车以恒定的加速度启动
机车以不变的加速度做匀加速启动,其过程分析如下表所示:
机车匀加速启动,牵引力不变速度增大,瞬时功率增大,当达到额定功率时,由于牵引力大于阻力,所以机车并没有达到最大速度,此后将保持功率不变做加速度逐渐减小的变加速运动,当牵引力与阻力大小相等时,加速度减小到零,机车才达到最大速度而匀速行驶。
例:汽车发动机的功率
p=60kw,若其总质量为m=5t,在水平面上行驶时,所受阻力恒为F=5.0×103N,试求:(1)汽车保持恒定功率启动时:①汽车所能达到的最大速度vmax,
②当汽车加速度为2m/s2时,速度是多大?③当汽车速度是6m/s时加速度是多大?
(2)若汽车以a=0.5m/s2的加速度由静止开始做匀加速运动,这一过程能维持多长时间?
思路分析:汽车在运动中所受的阻力大小为:F=5×103N
(1)汽车保持恒定功率启动时,做加速度逐渐减小的加速运动,当加速度减小到零时,速度达到最大
①当a=0时速度最大,所以,此时汽车的牵引力为F1=F=5×103N
则汽车最大速度
vmax==m/s=12m/s
②当汽车加速度为2m/s2时牵引力为F2,由牛顿第二定律得:
F2-F=ma
F2=F+ma=5×103N+5×103×2
N=1.5×104N
汽车的速度
v==m/s=4m/s
③当汽车速度是6m/s时牵引力为
F3==N=1×104N
由牛顿第二定律得:
F3-F=ma
汽车加速度为a==m/s2=1
m/s2
(2)当汽车以恒定的加速度a=0.5m/s2匀加速运动时,汽车的牵引力为F4,由牛顿第二定律得:
F4-F=ma
F4=F+ma=5×103N+5×103×0.5
N=7.5×103N
汽车匀加速运动时,其功率逐渐增大,当功率增大到等于额定功率时,匀加速运动结束,此时汽车的速度为
vt==m/s=8m/s
则汽车匀加速运动时间为
t==s=16s
规律技巧总结:
(1)无论哪种启动方式,机车所能达到的最大速度均为vmax=
P额为汽车的额定功率,F阻为汽车所受的所有阻力
(2)以恒定功率启动,速度增加,牵引力减小,合外力减小,加速度减小,是变加速运动,加速度与合外力的同时性是解题的关键。
(3)汽车以恒定的加速度启动时,汽车的功率逐渐增大,当功率增大到额定功率时,合外力结束,此时汽车的速度为匀加速运动的末速度,但不是汽车所能达到的最大速度,此后汽车还可以保持功率不变做加速度逐渐减小的加速运动,直大加速度减小到零时速度才达到最大。
功率p
一定
启动v
牵引力
F
阻力F1不变
加速度
a
变加速直线运动
F=F1时
a=0
达到最大速度vmax
匀速直线运动
P>
p额继续匀加速
F
a
达到最大速度vmax
变加速直线运动
达到p额时
F>F1
保持p额继续加速
v
加速度a
一定
v=at
速度
v
牵引力不变
P=Fv
功率
p
变加速直线运动
