18.1.2勾股定理
图片预览



文档简介
课件20张PPT。勾股定理 — 2勾股定理:直角三角形两直角边的平方和等于斜边的平方.活 动 1如果在Rt△ ABC中,∠C=90°,
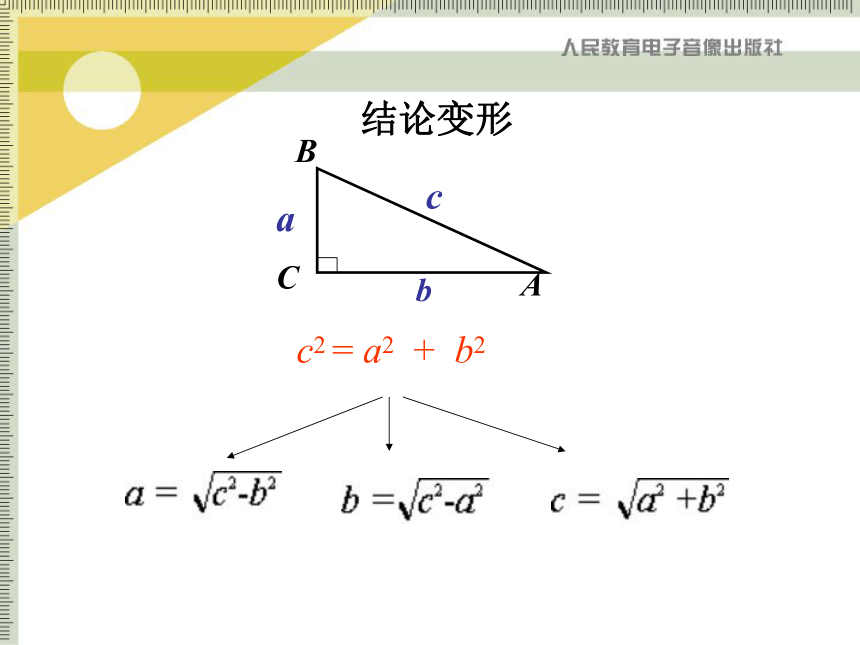
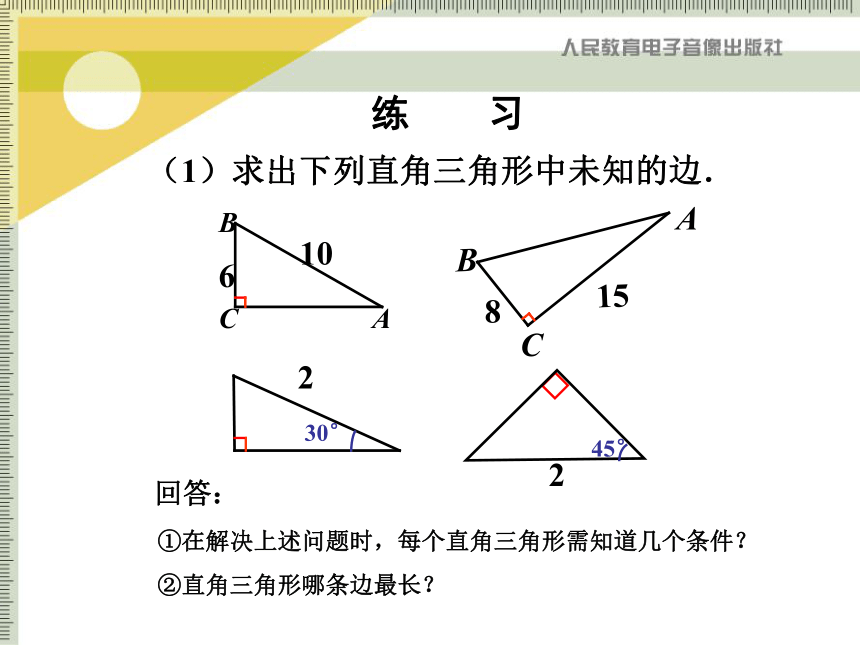
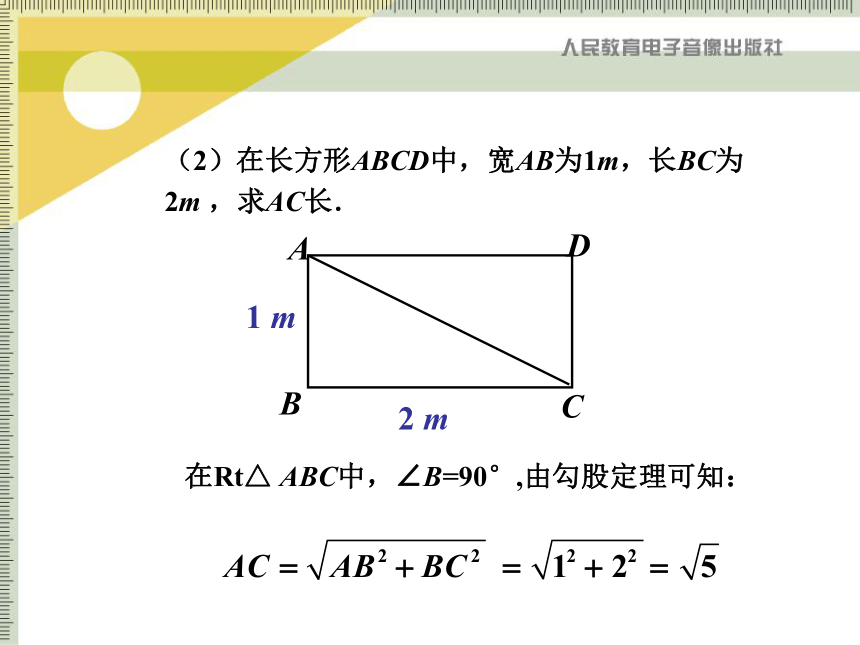
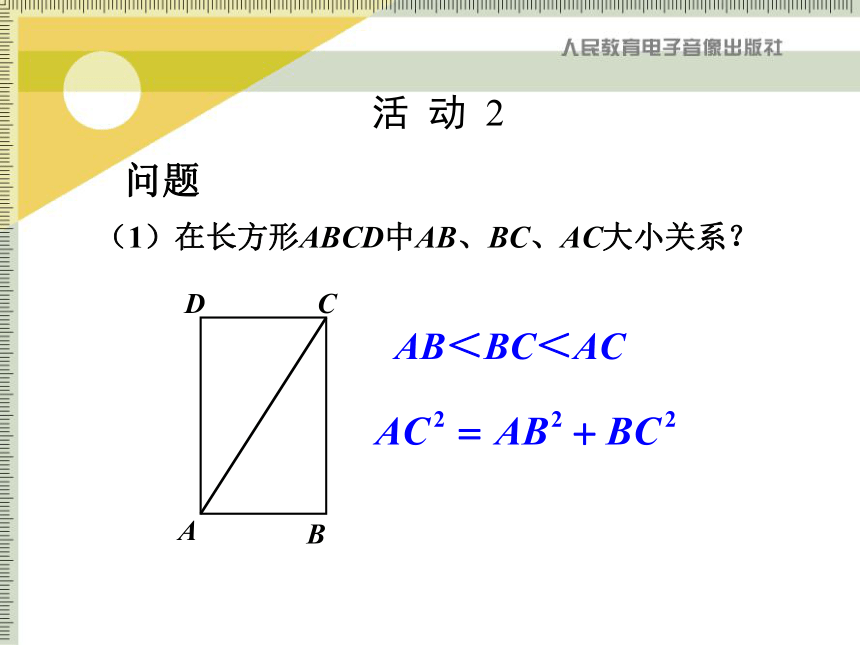
那么结论变形c2 = a2 + b2(1)求出下列直角三角形中未知的边.练 习回答:①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?(2)在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.1 m2 m在Rt△ ABC中,∠B=90°,由勾股定理可知:活 动 2问题(1)在长方形ABCD中AB、BC、AC大小关系?AB<BC<AC活 动 2(2)一个门框尺寸如下图所示.①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?②若薄木板长3米,宽1.5米呢?③若薄木板长3米,宽2.2米呢?为什么?1 m2 m∵木板的宽2.2米大于1米,
∴ 横着不能从门框通过;
∵木板的宽2.2米大于2米,
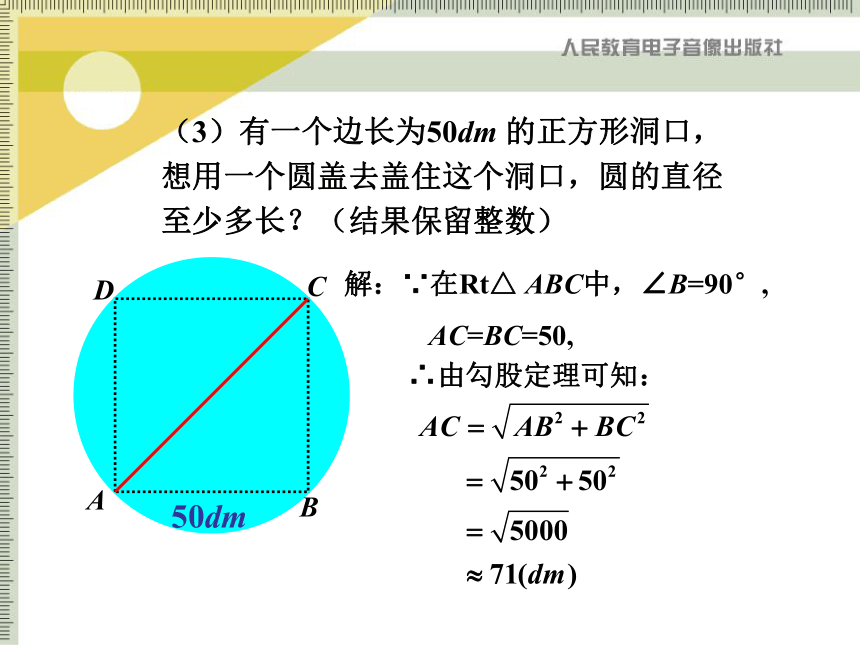
∴竖着也不能从门框通过.∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?(3)有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)50dmABCD解:∵在Rt△ ABC中,∠B=90°,
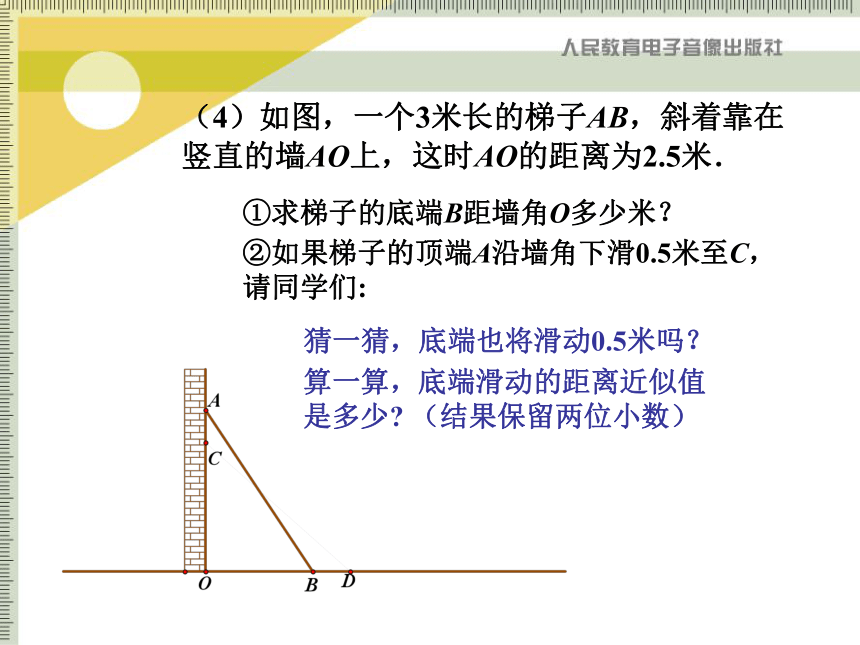
AC=BC=50,∴由勾股定理可知:(4)如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:猜一猜,底端也将滑动0.5米吗?算一算,底端滑动的距离近似值是多少? (结果保留两位小数)活 动 3(1)如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数)活 动 3(2)变式:以上题为背景,请同学们再设计其他方案构造直角三角形(或其他几何图形),测量池塘的长AB. 活 动 3(3)如图,分别以Rt △ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式为 . 活 动 3(3)变式:你还能求出S1、S2、S3之间的关系式吗?活 动 4(1)这节课你有什么收获? (2)作业①教材第78 页习题第2、3、4、5题.
②教材第79页习题第12题.补充练习及书后部分习题1.在Rt△ABC中, ∠C=90°,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b;
已知: a=7, c=8, 求b .2 .一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.3.如图,受台风“麦莎”影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?应用知识回归生活4.如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.40应用知识回归生活 5.小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕,发现屏幕只有58厘米长和46厘米宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?应用知识回归生活 6.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
那么结论变形c2 = a2 + b2(1)求出下列直角三角形中未知的边.练 习回答:①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?(2)在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.1 m2 m在Rt△ ABC中,∠B=90°,由勾股定理可知:活 动 2问题(1)在长方形ABCD中AB、BC、AC大小关系?AB<BC<AC活 动 2(2)一个门框尺寸如下图所示.①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?②若薄木板长3米,宽1.5米呢?③若薄木板长3米,宽2.2米呢?为什么?1 m2 m∵木板的宽2.2米大于1米,
∴ 横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?(3)有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)50dmABCD解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,∴由勾股定理可知:(4)如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:猜一猜,底端也将滑动0.5米吗?算一算,底端滑动的距离近似值是多少? (结果保留两位小数)活 动 3(1)如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数)活 动 3(2)变式:以上题为背景,请同学们再设计其他方案构造直角三角形(或其他几何图形),测量池塘的长AB. 活 动 3(3)如图,分别以Rt △ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式为 . 活 动 3(3)变式:你还能求出S1、S2、S3之间的关系式吗?活 动 4(1)这节课你有什么收获? (2)作业①教材第78 页习题第2、3、4、5题.
②教材第79页习题第12题.补充练习及书后部分习题1.在Rt△ABC中, ∠C=90°,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b;
已知: a=7, c=8, 求b .2 .一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.3.如图,受台风“麦莎”影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?应用知识回归生活4.如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.40应用知识回归生活 5.小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕,发现屏幕只有58厘米长和46厘米宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?应用知识回归生活 6.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
