第一章机械振动 复习课1 课件

课件40张PPT。第1章 阶段复习课 及时回顾基础有助于提升学科综合素养。本栏目精心梳理单元主干基础知识，系统全面、层次清晰，便于快速回顾、高效理解，以达事半功倍之目的。一、弹簧振子
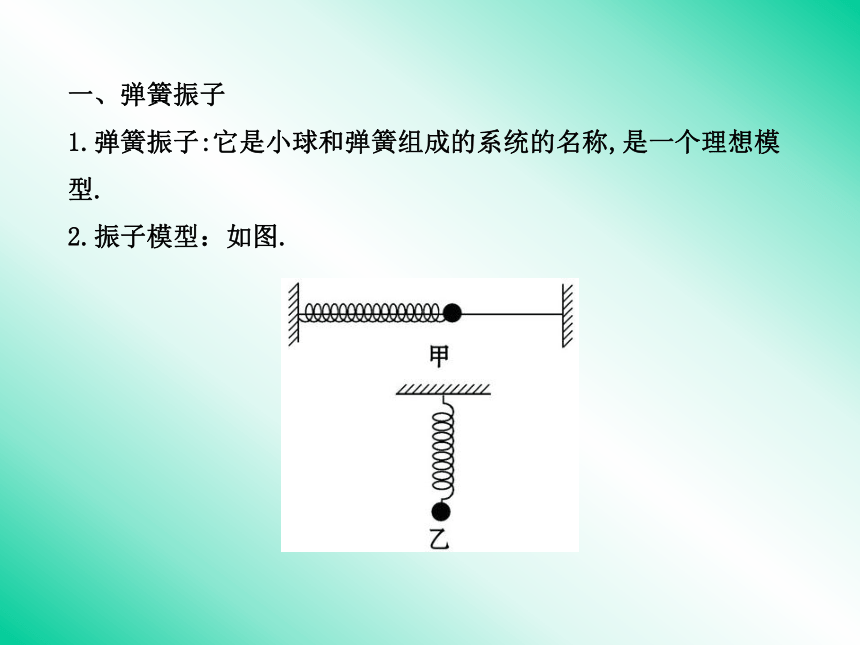
1.弹簧振子:它是小球和弹簧组成的系统的名称,是一个理想模型.
2.振子模型：如图. 3.弹簧振子应满足以下条件
（1）质量:弹簧质量比小球质量小得多,可以认为质量只集中于振子（小球）上.
（2）体积:弹簧振子中与弹簧相连的小球的体积要足够小,可以认为小球是一个质点.
（3）阻力:在振子振动过程中,忽略弹簧与小球受到的各种阻力.
（4）弹性限度:振子从平衡位置拉开的最大位移在弹簧的弹性限度内. 二、机械振动的位移
1.振动位移是从平衡位置指向振子某时刻所在位置的有向线段，方向为平衡位置指向振子所在位置，大小为平衡位置到该位置的距离.
2.振动位移也是矢量，若规定振动质点在平衡位置右侧时位移为正，则它在平衡位置左侧时位移就为负. 3.位移的表示方法（图）：以平衡位置为坐标原点，以振动所在的直线为坐标轴，规定正方向，用振动图象中该时刻振子所在的位置坐标来表示.在t1时刻振子的位移为x1,t2时刻振子的位移为x2,t4时刻为-x4.4.区别机械运动中的位移：
机械运动中的位移是从初位置到末位置的有向线段；在简谐运动中，振动质点在任意时刻的位移总是相对于平衡位置而言的，都是从平衡位置开始指向振子所在位置.三、回复力
1.回复力是指将振动的物体拉回到平衡位置的力，是按照力的作用效果来命名的，分析物体的受力时，不分析回复力.
2.回复力可以由某一个力提供（如弹力、摩擦力等），也可能是几个力的合力，还可能是某一力的分力，归纳起来回复力一定等于物体在振动方向上所受的合力. 3.简谐运动的回复力：F=-kx.
（1）由F=-kx知，简谐运动的回复力大小与振子的位移大小成
正比，回复力的方向与位移的方向相反，即回复力的方向总是
指向平衡位置.
（2）公式F=-kx中的k指的是回复力与位移间的比例系数，而不
一定是弹簧的劲度系数，系数k由振动系统自身决定.
（3）据牛顿第二定律， 表明弹簧振子做简谐运动
时振子的加速度大小也与位移大小成正比，加速度方向与位移
方向相反. 四、单摆
1.运动特点
（1）摆球以悬点为圆心做变速圆周运动,因此在运动过程中只要速度v≠0,半径方向都受向心力.
（2）摆球同时以平衡位置为中心做往复运动,因此在运动过程中只要不在平衡位置,轨迹的切线方向都受回复力. 2.摆球的受力
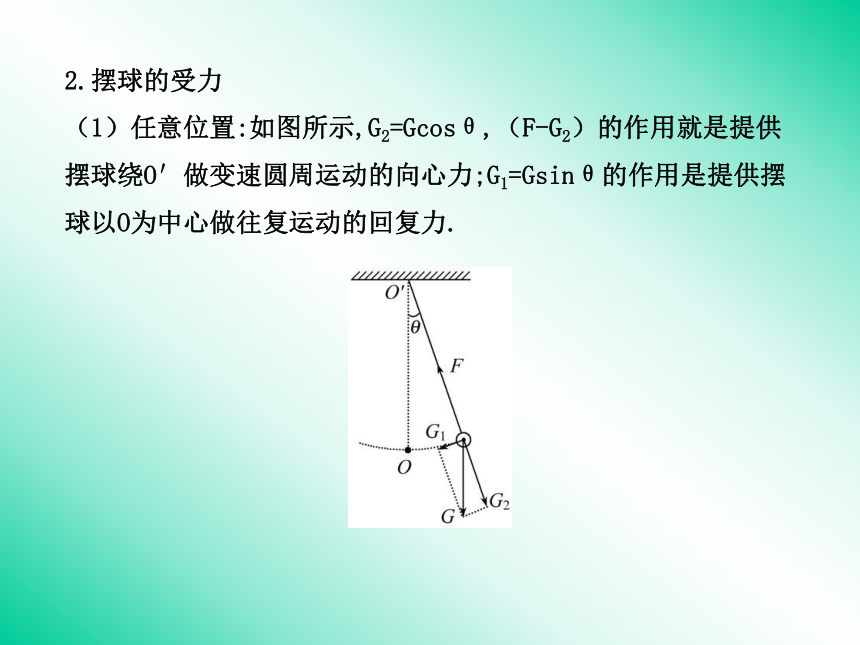
（1）任意位置:如图所示,G2=Gcosθ,（F-G2）的作用就是提供摆球绕O′做变速圆周运动的向心力;G1=Gsinθ的作用是提供摆球以O为中心做往复运动的回复力. （2）平衡位置:摆球经过平衡位置时,G2=G,G1=0,此时F大于G,
（F-G）的作用提供向心力;因在平衡位置,回复力F回=0与G1=0相
符.
（3）单摆的简谐运动
在θ很小时（理论值为5°）, 那么重力沿切线方向
上的分力的大小为 G1方向与摆球位移方向相
反,所以有回复力 .因此,在摆角θ很小时,
单摆做简谐运动. 五、单摆的周期
1.单摆周期的影响因素
（1）单摆的周期与单摆的振幅无关,与摆球的质量无关.
（2）单摆的周期与摆长有关,摆长越长,周期越大.
2.单摆的周期公式：六、简谐运动、阻尼振动与受迫振动的区别
简谐运动是一种理想化的模型，物体运动过程中的一切阻力都不考虑，阻尼振动却考虑阻力的影响，是更实际的一种运动，而受迫振动则是物体做阻尼振动时受到周期性驱动力作用下的振动，三者对比列表如下： 振动类型 比较项目 振动类型 比较项目 对所学知识及时总结，将其构建成知识网络，既有助于整体把握知识结构，又利于加深对知识间内在联系的理解。下面是本阶段的知识结构图，请要求学生认真填一填吧！一、关于平衡位置需认清的几个问题
1.平衡位置是回复力为零的位置.
2.平衡位置不一定是合力为零的位置，当摆球运动到平衡位置时单摆受力是不平衡的；处在加速上升电梯里的单摆停止摆动仍存在向上的加速度，受力是不平衡的.3.不同振动系统平衡位置不同：弹簧振子处于平衡位置时，弹簧不一定处于原长，比如在竖直方向的弹簧振子，平衡位置是其弹力等于重力的位置；而单摆的平衡位置也不一定是在竖直的最低点，如在水平匀强电场和重力场共同作用下的单摆，平衡位置在电场力与重力的合力方向上.【典例1】若物体做简谐运动，则下列说法中正确的是（ ）
A.若物体经过关于平衡位置对称的两点时，速度一定相同，加速度方向相反
B.物体通过平衡位置时，所受合力为零，回复力为零，处于平衡状态
C.物体每次通过同一位置时，其速度不一定相同，但动能一定相同
D.物体的位移增大时，动能增加，势能减少
【规范解答】选C.可借助于弹簧振子和单摆这两个做简谐运动的模型来研究．如图甲所示，选水平向右为正方向，振子经过关于平衡位置对称的两点时，速度大小相等，方向可能不同，选项A错误；物体通过平衡位置时，F回＝0，但合力不一定为零，如图乙所示，单摆摆球通过平衡位置时，沿悬线方向有加速度，F合≠0，选项B错误；物体通过同一位置时，速度方向有两种可能，故速度不一定相同，但物体的动能一定相同，选项C正确；做简谐运动的物体机械能守恒，其位移增大时，势能增加，动能减少，选项D错误.【变式训练】如图所示，A、B叠放在光滑水平地面上，B与自由
长度为L0的轻弹簧相连，当系统振动时，A、B始终无相对滑
动，已知mA＝3m，mB＝m，当振子距平衡位置的位移 时，
系统的加速度为a，求A、B间摩擦力f与位移x的函数关系.【解析】设弹簧的劲度系数为k，以A、B整体为研究对象，系统
在水平方向上做简谐运动，其中弹簧的弹力作为系统的回复
力，所以对系统运动到距平衡位置 时， ①
当系统的位移为x时，A、B间的静摩擦力为f，此时A、B具有共
同加速度a′，对系统有
kx＝（mA＋mB）a′ ②
对A有f=mAa′ ③
联立①②③得
答案：二、简谐运动的对称性问题
1.相隔T/2或（2n＋1）T/2（n为正整数）的两个时刻，振子位置关于平衡位置对称．位移、速度、加速度大小相等，方向相反.
2.质点在距平衡位置等距离的两个点上具有相等大小的速度、加速度，在平衡位置左右相等的距离上运动时间也是相同的. 【典例2】一弹簧振子做简谐运动，其振动图象如图所示，那么
在（ ）和（ ）（Δt是微小的时间）两时刻，振子
的：①速度相同；②加速度相同；③相对平衡位置的位移相
同；④振动的能量相同．以上叙述中正确的是（ ）
A．①② B.②③ C.③④ D.①④【规范解答】选D.在（ ）时刻，振子正在沿x负方向向平
衡位置运动，加速度沿x负方向指向平衡位置，位移为正,
（ ）时刻，振子正沿x负方向远离平衡位置运动，加速度
沿x正方向指向平衡位置，位移为负，根据对称性，两个时刻速
度相同，简谐振动的机械能守恒，因此两个时刻的能量相同,故
D正确,A、B、C错误 【变式训练】如图所示为一弹簧振子的振动图象，由此可知 （ ）
A.在t1时刻，振子的动能最大，所受的弹性力最大
B.在t2时刻，振子的动能最大，所受的弹性力最小
C.在t3时刻，振子的动能最大，所受的弹性力最小
D.在t4时刻，振子的动能最大，所受的弹性力最大【解析】选B.从图象的横坐标和纵坐标可以知道此图象是机械振动图象，它所描述的是一个质点在不同时刻的位置.t2和t4时刻振子在平衡位置处，t1和t3时刻振子在最大振幅处，头脑中应出现一幅弹簧振子振动的实物图象.根据弹簧振子振动的特征，弹簧振子在平衡位置处的速度最大，加速度为零，即弹性力为零，在最大位置处，速度为零，加速度最大，即弹性力最大，所以B正确.三、单摆周期公式 中的有关问题
1.单摆周期公式中的g
（1）只受重力和绳拉力，且悬点静止或做匀速直线运动的单
摆，g为当地重力加速度，在地球上不同位置g的取值不同，不
同星球表面g值也不相同.
（2）单摆处于超重或失重状态，等效重力加速度g＝g0±a，如
在轨道上运动的卫星a＝g0，完全失重，等效g＝0. 2.含有其他作用力的单摆的周期
（1）若该作用力对单摆的回复力没有影响，则周期仍然不变．如悬点处有带正电的点电荷，而摆球带正电，此时库仑力沿摆线方向，不影响回复力，周期与不带电时一样.
（2）若该作用力为一恒力，等效g的取值为单摆不摆动时，摆线的拉力F与摆球质量m的比值，即等效g＝F/m. 【典例3】光滑斜面倾角为θ，斜面上有一辆挂有单摆的小车，如图所示，在小车下滑过程中单摆同时摆动，已知摆长为L，求单摆的振动周期.【规范解答】单摆处于失重状态，当单摆与小车相对静止加速
下滑时，悬线拉力为F＝mgcosθ，故单摆做简谐运动时的等效
加速度g′＝gcosθ，如图所示，故振动周期
答案：【变式训练】如图所示,将摆长为l的单摆放在一升降机中,若升降机以加速度a向上匀加速上升,求单摆的摆动周期.【解析】单摆的平衡位置在竖直位置,若摆球相对升降机静止,
则单摆受重力mg和绳拉力F,根据牛顿第二定律得:F-mg=ma.此时
摆球的视重mg′=F=m（g+a）.所以,单摆的等效重力加速度
因而单摆的周期
答案：四、共振问题
1.共振是本章的重点之一,共振的产生条件、共振的现象及共振曲线应该熟练掌握,并能应用其解决问题.
2.解决共振问题的关键是抓住共振的条件,即驱动力的频率等于固有频率. 【典例4】如图所示是一个单摆做受迫振动时的共振曲线，表示振幅A与驱动力的频率f的关系，下列说法正确的是（ ）
A.摆长约为10 cm
B.摆长约为1 m
C.若增大摆长，共振曲线的“峰”将向右移动
D.若增大摆长，共振曲线的“峰”将向左移动 【规范解答】选B、D.由单摆做受迫振动时的共振曲线可知，当单摆发生共振时，固有频率等于驱动力的频率，即固有频率为0.5 Hz，因而固有周期为2 s，由单摆的周期公式可知，此单摆的摆长约为1 m，B正确；若增大摆长，周期变长，频率变小，共振曲线的“峰”将向左移动，D正确.【变式训练】在接近收费口的道路上安装了若干条突起于路面
且与行驶方向垂直的减速带，减速带间距为10 m，当车辆经过
减速带时会产生振动，若某汽车的固有频率为1.25 Hz，则当该
车以_______ m/s的速度行驶在此减速区时颠簸得最厉害，我们
把这种现象称为_________.
【解析】汽车在减速带的作用下，做周期性的振动， 当
振动周期T等于固有周期时，即 时发生共振，
答案：12.5 共振