1.3 单摆 课件 (2)

课件17张PPT。1.3 单摆 课件1.单摆在细线的一端拴上一个小球，另一端固定在悬点上，如果线的伸缩和质量可以忽略不计，球的直径比线长短得多，这样的装置叫单摆．
悬点：固定
细线：不可伸缩．质量不计．长．
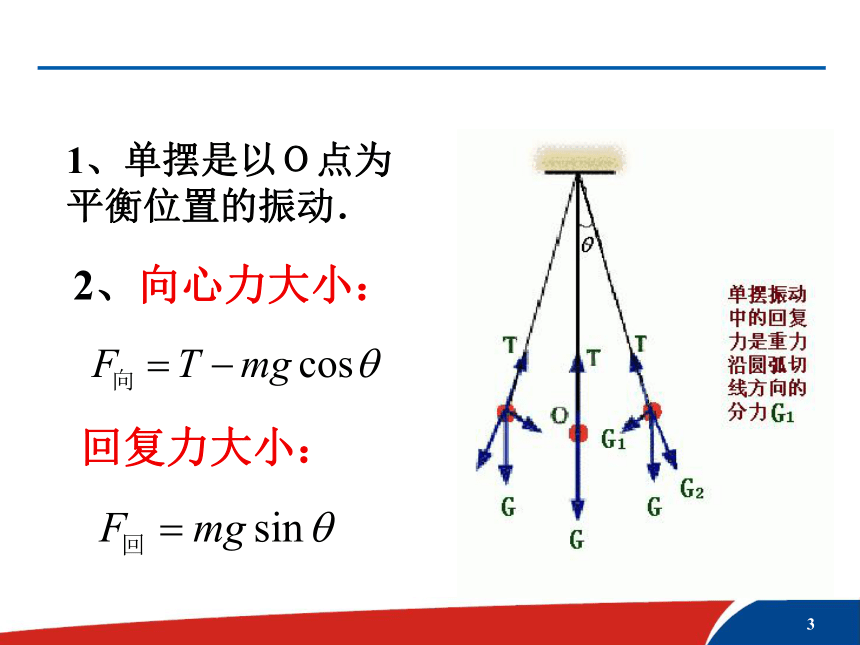
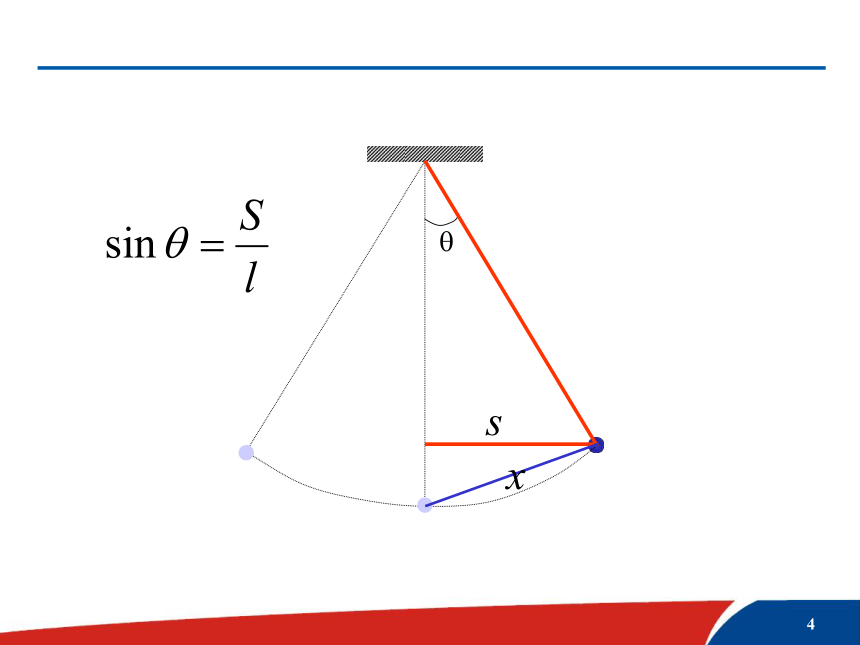
摆球：小．质量大单摆的振动回复力大小：2、向心力大小：1、单摆是以Ｏ点为平衡位置的振动．?xs仔细观察下面表格：你能得到什么结论？ 当θ角很小（ θ＜5° ）时，角的正弦值近似等于θ所对应的弧度值，即sinθ≈θ??很小时：x单摆做简谐运动的条件回复力大小：?很小时：在摆角很小的情况下 （?＜5°） ，单摆所受回复力跟位移成正比且方向相反，单摆做简谐运动． 猜想：
（1）摆球质量m
（2）振幅A（摆角θ）
（3）摆长L
（4）重力加速度g
实验方法：控制变量法
如何设计实验方法？
实验验证：实验与探究：探究单摆周期与哪些因素有关 实验结论：
（1）单摆振动的周期与摆球质量无关，当摆角θ<5°时，单摆振动的周期与振幅无关（单摆的等时性）
（2）单摆振动的周期与摆长有关，摆长越长，周期越大
（3）单摆振动的周期与重力加速度有关，重力加速度越大，周期越小实验与探究：探究单摆周期与哪些因素有关 T与l的定量关系做出如下猜测：T∝l，T∝ l2，T∝ l1/2 …… 如何确定关系？
作出图像，如果是过原点的直线则成正比 实验与探究：探究单摆周期与摆长的定量关系荷兰物理学家惠更斯单摆做简谐运动的周期T跟摆长l的算术平方根成正比，跟重力加速度g的算术平方根成反比，跟振幅、摆球的质量无关．单摆的周期公式l：摆长(悬点到小球重心的距离)g：当地重力加速度单摆的应用１．利用它的等时性计时．２．测定重力加速度． 惠更斯在1656年首先利用摆的等时性发明了带摆的计时器（1657年获得专利权）．单摆小结3、在摆角小于５°时，回复力Ｆ≈－ x，单摆的振动可看成简谐运动4、单摆的振动周期跟振幅、摆球质量的大小无关，跟摆长的平方根成正比，跟重力加速度的平方根成反比，即
T＝2π 1、单摆是一种理想化的物理振动模型
2、单摆振动的回复力是由摆球重力沿圆弧切线方向的分力mgsinθ提供的. 1862年，18岁的伽利略离开神学院进入比萨大学学习医学，他的心中充满着奇妙的幻想和对自然科学的无穷疑问，一次他在比萨大学忘掉了向上帝祈祷，双眼注视着天花板上悬垂下来摇摆不定的挂灯，右手按着左手的脉搏，口中默默地数着数字，在一般人熟视无睹的现象中，他却第一个明白了挂灯每摆动一次的时间是相等的，于是制作了单摆的模型，潜心研究了单摆的运动规律，给人类奉献了最初的能准确计时的仪器. 探究单摆周期与摆长的定量关系 实验步骤1、如图制作单摆：细线上端 在铁架台上，下端系一个小球3、将小球拉至某高度（摆角＜5°），使其在竖直平面内摆动2、记下摆长=细线长度（刻度尺）+小球半径（游标卡尺测直径）4、测量周期T：以最低点为计时开始测量单摆做50次全振动的时间，算出周期细线上端的悬挂方式 如甲、乙两图画出了细线上端的两种不同的悬挂方式，哪种比较好？为什么？制作中还要注意：
1、摆线尽量细长些，伸缩性小些，摆球质量尽量大些，体积小些，否则不是单摆.
2、摆的振幅不要太大，否则摆的振动不是简谐运动周期测量要点2、全振动1、摆球摆到哪个位置的时刻 作为计时开始与停止的时刻 2、此时由于最低点速度大，相应经过同样位移时的时间误差就小.1、到达最高点的位置不容易判断，在最低点容易判断