2.3 波的干涉和衍射 课件 (3)

课件39张PPT。2.3 波的干涉和衍射波的干涉
一、波的迭加原理
实验证明：
当介质中存在两个以上的波源时，这时各波源所激起的波可在同一介质中独立地传播；而在各个波相互交迭的区域，各点的振动(位移或电磁场)则是各个波在该点激起的振动的矢量和。
例如：(1)几个水波可以互不干扰地相互贯
穿，然后继续按各自原来方式传播；
(2)当交响乐队演奏时，人耳仍能清
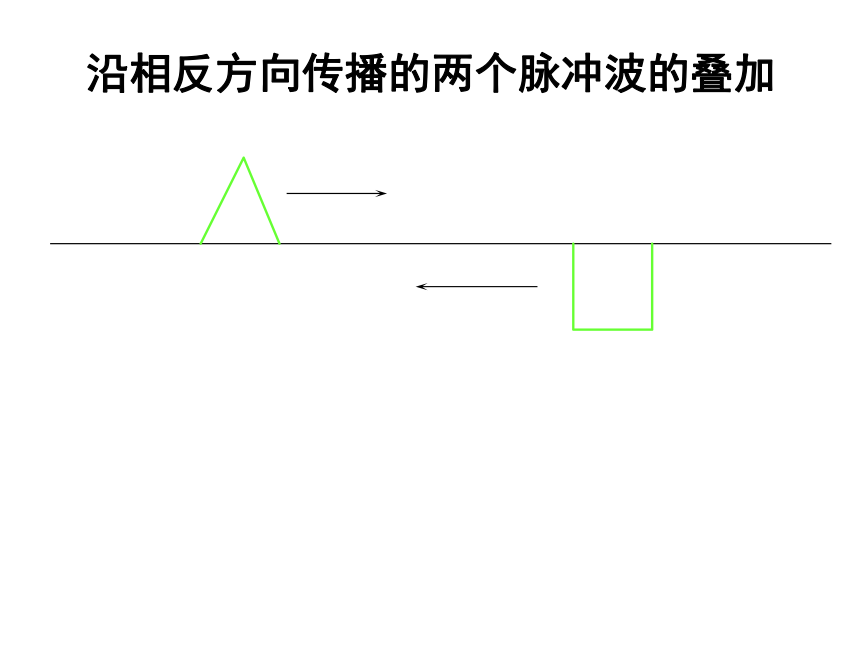
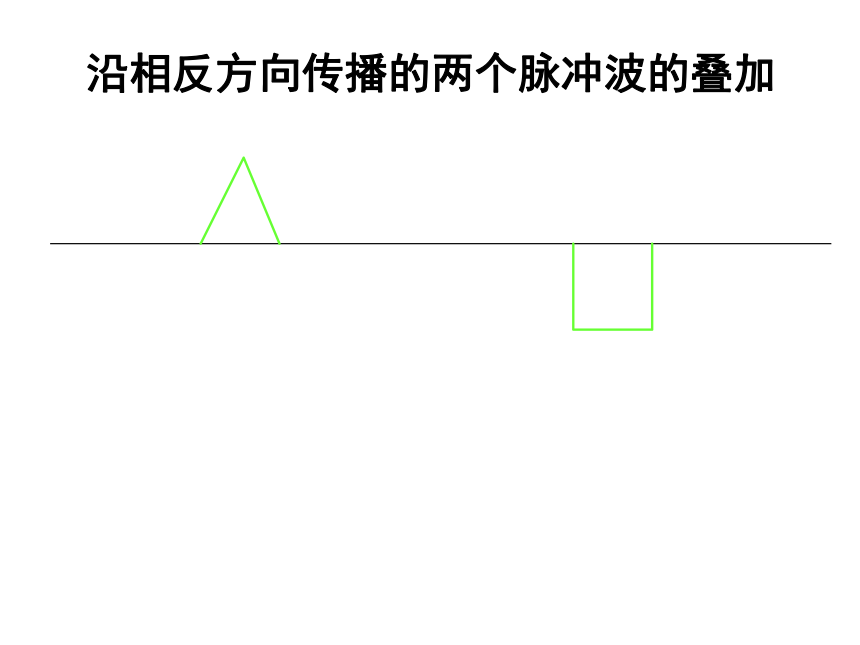
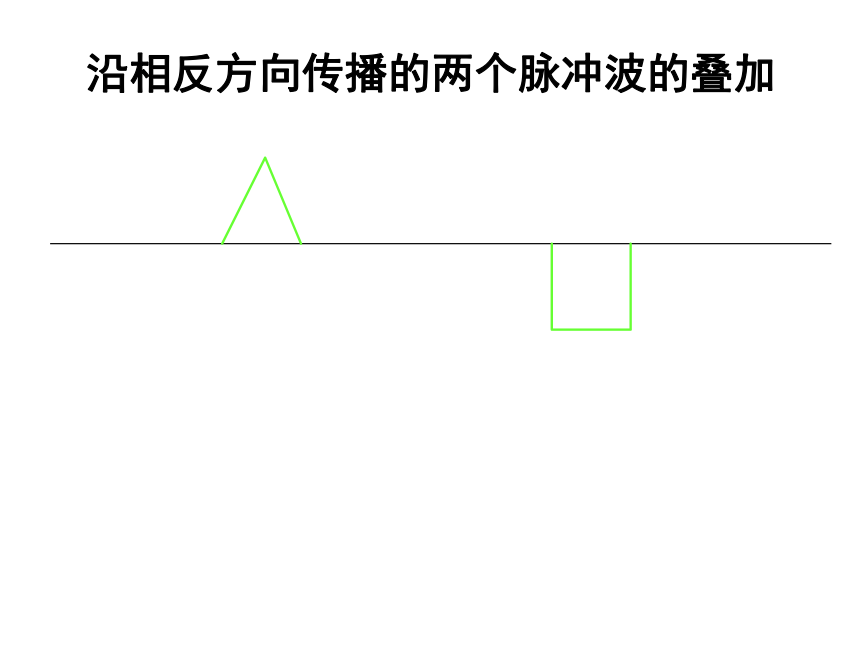
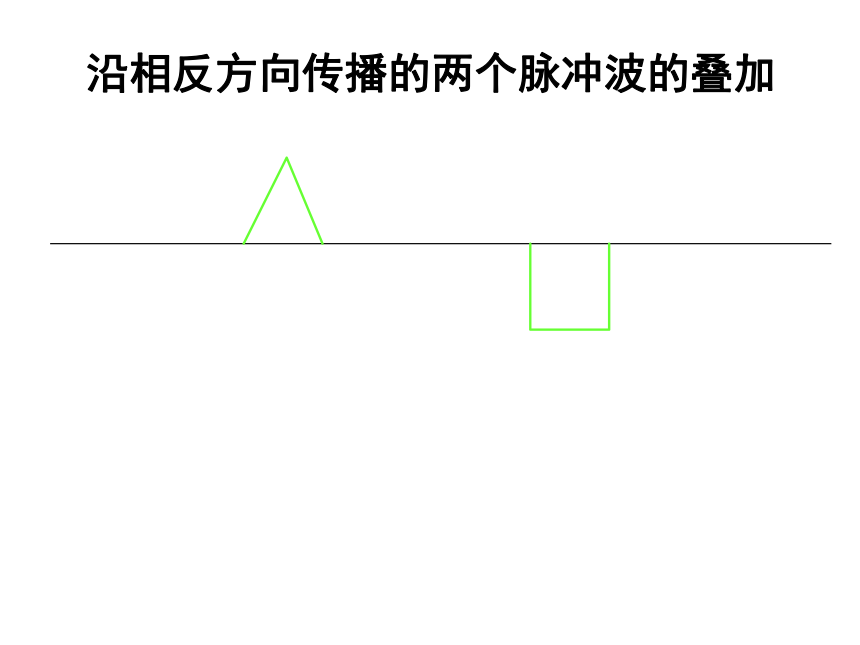
晰地分辨出每个乐器演奏的旋律。两水波的叠加SS12沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加沿相反方向传播的两个脉冲波的叠加二、波的干涉
1、相干源?
两个频率相同，振动方向相同、相位相同或相位差恒定的波源。
干涉现象：
两个相干源波在空间迭加时，在某些点处振动始终加强，而在另一些点处，振动始终减弱。
光既然是电磁波，也能产生干涉现象。光的相干性：
(1) 两独立的光源不可能成为一对相干光源
原因：原子发光是随机的，间歇性的，两
列光波的振动方向不可能一致，周
相差不可能恒定。(2) 同一光源上两个不同的部分，也不可
能得到相干光源。?相干光实现方法：
为了利用普通光源( 除激光外 )获得相干光，其基本方法是把由同一光源上同一点发出的光，设法分成两部分。
(1)分波阵面法
从光源发出的同一列波的波面上分割出两个微小的部分(例如双孔干涉)，这两个微小部分可以看作两个子光源，它们发出的光是相干光。(2)分振幅法
设法把同一波列(一个分子或原子在持续时间内发出的光波)的光波通过反射或折射等过程，分成两束光波(例如薄膜干涉)。显然，这两列光波是相干光波，它们的能量是从同一波列的光波分出来的。
激光是目前最理想的相干光源，它不仅同一光源上同一点发出的是相干光，而且同一光源上两个不同的部分也具有很好的相干性，甚至两个独立激光器的光波也能相干。y10 = A10 cos ( 2??t +φ1 )
y20 = A20 cos ( 2??t +φ2 )?
S1 和 S2 发出的波到达 P点的振动分别为：
y1 = A1 cos ( 2??t +φ1 - 2? r1 /λ)
y2 = A2 cos ( 2??t +φ2 - 2? r2 /λ)?
两个振动在 P点的相位差为：?
Δφ=φ2 -φ1 - 2? ( r2 - r1 ) /λ
P 点的振动就是这两个振动的合振动。2、两个相干源的干涉
设波源 S1、S2的振动方程为：P点合振动：
频率 — 两同频率、同方向振动的合振动仍
为同频率的振动；
振幅 — 由两分振动的相位差来决定。由于
两波源的相位差φ2 -φ1是恒定的，
因此，空间中任一 P点两振动的相
位差也是恒量，所以，任一P点合
振幅也是恒量。干涉加强与减弱条件：
加强：Δφ=φ2 -φ1 - 2? ( r2 - r1 ) /λ
= ± 2k? (k = 0，1，2，3…)
合振幅 A 最大，A = A1 + A2 。
减弱：Δφ= φ2 -φ1 - 2? ( r2 - r1 ) /λ
=±(2k+1)? (k = 0，1，2，3…)
? 合振幅A为最小， A = |A1 - A2| 。?
如果φ1=φ2，上述条件可简化为波程差δ：
加强：δ= r2 - r1 = ±2k (λ/ 2)
( k = 0，1，2…) 又称为干涉相长减弱：δ= r2 - r1 = ±( 2k + 1 ) (λ/ 2 )
（k = 0，1，2… ) 又称为干涉相消x例10-4 杨氏双孔干涉
实 验 现 象解：S 是单色点光源，在遮光屏 B 上开两小孔 S1，S2 作为相干光源。
设 S 到 S1 和 S2 的距离相等，则 S1和 S2可看作两个相位相同的相干光源。
问题的关键是计算从 S1和 S2到 P (x , y)点的波程差 δ= r2 - r1。?通常 D >> d，由几何关系可得：
r12 = D2 + ( x - d/2 )2 + y2
r22 = D2 + ( x + d/2 )2 + y2
两式相减后，得：?
r22 - r12 = ( r2 - r1 ) ( r2 + r1 ) = 2dx?r22 - r12 = ( r2 - r1 ) ( r2 + r1 ) = 2dx?
因 D >> d ? r2 + r1 ? 2r
波程差： δ= r2 - r1 ? d x / r
当 x << D 时，r ? D
波程差： δ= r2 - r1 ? d x / D? 波程差：δ= r2 - r1 ? d x / D
P点干涉加强的条件为：?
δ ? d x / D = ± 2k (λ/2 )
明条纹中心的位置：
x = ±k Dλ/ d? ( k = 0，1，2，3… )
其中 k 叫做明条纹的级次。
由于上式表示一条直线方程，所以两孔干涉在光屏上的明条纹为等间隔直条纹。
相邻明条纹的间距为： Δx = Dλ/ d?同理可得暗纹中心的位置：?
x =±(2k + 1)Dλ/2d ( k = 0，1，2，3… )
暗条纹也是等间隔直条纹，相邻间距与明条纹一样。
如果用白光做实验，则除了 k = 0 级次(中央明纹)的中部为白色外，其他各级次明纹将因不同波长(色光)的极大在不同位置而变成彩色。?
著名的杨氏双孔实验，证实光的波动性。
后来狭缝代替针孔称为双缝实验可得更清晰且明亮干涉图样，请同学们想想其中的原因。 思 考 题
在杨氏双孔实验（D ? d）中，如果点光源 S
1、沿垂直画面方向作微小位移，
2、沿平行于 S1S2 连线方向作微小位移，
问：屏上的干涉条纹将会如果变化？四、薄膜干涉
1、光程和光程差?
前面讨论波的干涉条件时，仅限于相干波在同一介质内传播的情况。下面将讨论相干光经过不同介质后产生的干涉现象光程：?
光在折射率为 n 的介质中传播，通过几何路程为 x，则光的相位改变了：
Δφ= 2?x / ?’ ( ?’为介质中的波长)
Δφ = 2? nx / ? ( ? 为真空中的波长) Δφ = 2? nx / ? ( ? 为真空中的波长)
定义：光程 = n x，即折算到真空中的路程。Δφ与光程差δ之间的关系：
Δφ=2?δ/ ?
同相位的相干光，明暗条纹的干涉条件：
Δφ=2?δ/? = ± 2k? （明条纹）
Δφ=2?δ/? = ± (2k + 1)? （暗条纹）
用光程差δ来表示，即：?
δ= ± 2k ? / 2? （明条纹）
δ= ± ( 2k + 1) ? / 2 （暗条纹）
其中 k = 0，1，2，3… 。