整数指数幂1
图片预览







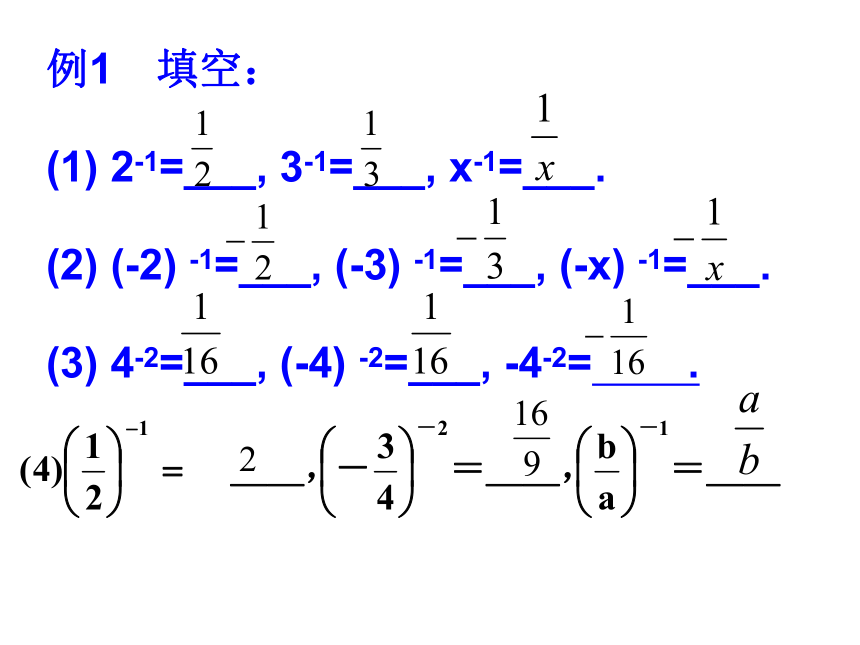

文档简介
课件25张PPT。16.2.3整数指数幂(1)an=a·a·a········a(n是正整数)幂an的意义是什么?n个a正整数指数幂:an(n是正整数)(3) ( n是正整数) (1) (m、n是正整数) (a≠0,m、n是
正整数,m>n) 正整数指数幂有以下运算性质:(2) (m、n是正整数) (5) ( n是正整数) 当a≠0时,a0=1。(0指数幂)一般地, 中指数m可以是负整数吗?如果可以,那么负整数指数幂 表示什么?
我们知道:即思考:am÷an=am-n (a≠0 m、n为正整数且m>n)a5÷a3a3÷a5=?分析a3÷a5=a3-5=a-2a3÷a5==规定:=a2)负指数幂的意义:一般地,当n是正整数时,这就是说:a-n(a≠0)是an的倒数例如:引入负整数指数幂后,指数的取值范围就扩大到全体整数。an (n是正整数)1 (n=0, a≠0 )例1 填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .(1) 30=___, 32=_____, 3-2=_____;
(2) (-3)0=___,(-3)2=____, (-3)-2=_____;
(3) b0=____, b2=_____, b-2=____(b≠0).练习口答例2、把下列各式转化为只含有正整数指数幂的形式1、a-32、x3y-23、2(m+n)-24、5、6、思考:引入负整数指数和0指数后,这条性质能否扩大到m、n是任意整数的情形?(m、n是正整数)正整数指数幂的运算性质是否适合负指数呢?这条性质对于m,n是任意整数的情形仍然适用。归纳(1)am·an=am+n (a≠0)整数指数幂有以下运算性质:(6)当a≠0时, a0=1。a-3·a-9=(2)(am)n=amn (a≠0) (3)(ab)n=anbn (a,b≠0)(4)am÷an=am-n (a≠0)(5) (b≠0)(a-3)2=(ab)-3=a-3÷a-5=例3. 计算:练习一口答(1) x2y-3(x-1y)3;
(2) (2ab2c-3)-2÷(a-2b)3练习二计算:思考:课堂练习1.计算:
(a+b)m+1·(a+b)n-1;
(2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
2.计算下列各式,并把结果化为只含 正整数指数的形式(4);(5).小结n是正整数时, a-n属于分式。并且(a≠0) 重点掌握整数指数幂的运算法则,注意运算性质及符号。1. P 23 习题16.2第7、15、16题作 业 2. 作业本(1)3. A本整数指数幂(1)再见
正整数,m>n) 正整数指数幂有以下运算性质:(2) (m、n是正整数) (5) ( n是正整数) 当a≠0时,a0=1。(0指数幂)一般地, 中指数m可以是负整数吗?如果可以,那么负整数指数幂 表示什么?
我们知道:即思考:am÷an=am-n (a≠0 m、n为正整数且m>n)a5÷a3a3÷a5=?分析a3÷a5=a3-5=a-2a3÷a5==规定:=a2)负指数幂的意义:一般地,当n是正整数时,这就是说:a-n(a≠0)是an的倒数例如:引入负整数指数幂后,指数的取值范围就扩大到全体整数。an (n是正整数)1 (n=0, a≠0 )例1 填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .(1) 30=___, 32=_____, 3-2=_____;
(2) (-3)0=___,(-3)2=____, (-3)-2=_____;
(3) b0=____, b2=_____, b-2=____(b≠0).练习口答例2、把下列各式转化为只含有正整数指数幂的形式1、a-32、x3y-23、2(m+n)-24、5、6、思考:引入负整数指数和0指数后,这条性质能否扩大到m、n是任意整数的情形?(m、n是正整数)正整数指数幂的运算性质是否适合负指数呢?这条性质对于m,n是任意整数的情形仍然适用。归纳(1)am·an=am+n (a≠0)整数指数幂有以下运算性质:(6)当a≠0时, a0=1。a-3·a-9=(2)(am)n=amn (a≠0) (3)(ab)n=anbn (a,b≠0)(4)am÷an=am-n (a≠0)(5) (b≠0)(a-3)2=(ab)-3=a-3÷a-5=例3. 计算:练习一口答(1) x2y-3(x-1y)3;
(2) (2ab2c-3)-2÷(a-2b)3练习二计算:思考:课堂练习1.计算:
(a+b)m+1·(a+b)n-1;
(2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
2.计算下列各式,并把结果化为只含 正整数指数的形式(4);(5).小结n是正整数时, a-n属于分式。并且(a≠0) 重点掌握整数指数幂的运算法则,注意运算性质及符号。1. P 23 习题16.2第7、15、16题作 业 2. 作业本(1)3. A本整数指数幂(1)再见
