1.1 简谐振动 学案

1．1《简谐振动》学案
【学习目标】
知道简谐振动的概念，掌握简谐振动图像的获取方法；
理解简谐振动的图像特点，会根据图像分析简谐振动；
3、知道周期、频率、振幅、位移等一系列描述简谐运动的基本概念。
【学习重点】
简谐振动的图像获取及分析、用函数及图像表达简谐运动、理解简谐振动的系列概念的物理意义。
【知识要点】
机械振动
（1）平衡位置：物体振动时的中心位置，振动物体未开始振动时相对于参考系静止的位置。
（2）机械振动：物体在平衡位置附近所做的往复运动，叫做机械振动，通常简称为振动。
（3）振动特点：振动是一种往复运动，具有周期性和往复性。
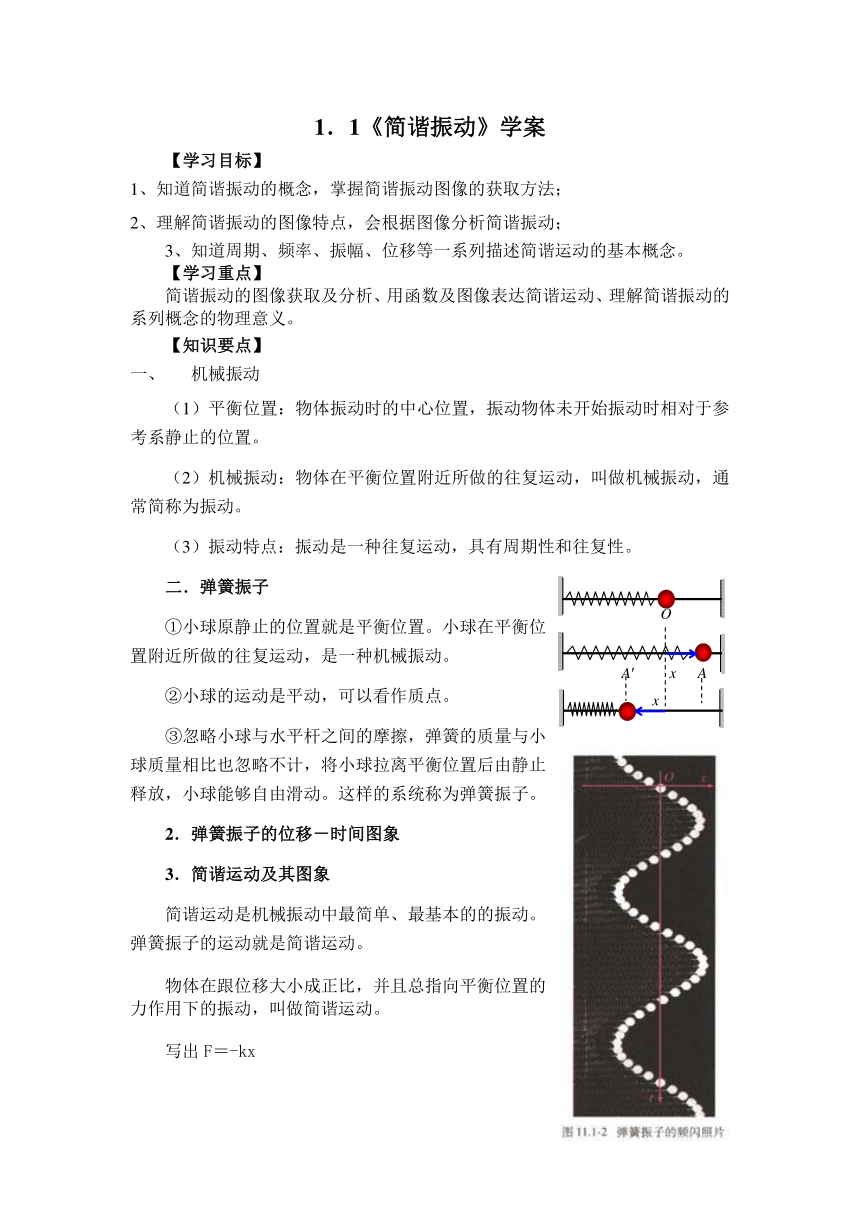
二．弹簧振子
①小球原静止的位置就是平衡位置。小球在平衡位置附近所做的往复运动，是一种机械振动。
②小球的运动是平动，可以看作质点。
③忽略小球与水平杆之间的摩擦，弹簧的质量与小球质量相比也忽略不计，将小球拉离平衡位置后由静止释放，小球能够自由滑动。这样的系统称为弹簧振子。
2．弹簧振子的位移－时间图象
3．简谐运动及其图象
简谐运动是机械振动中最简单、最基本的的振动。弹簧振子的运动就是简谐运动。
物体在跟位移大小成正比，并且总指向平衡位置的力作用下的振动，叫做简谐运动。
写出F＝-kx
说明式中F为回复力；x为偏离平衡位置的位移；k是常数，对于弹簧振子，k是劲度系数，对于其他物体的简谐运动，k是别的常数；负号表示回复力与位移的方向总相反。
质点的位移随时间按正弦规律变化的振动，叫做简谐运动。简谐运动的位移－时间图象为正弦曲线。
【典型例题】
例1、如图所示，在光滑水平面上，用两根劲度系数分别为k1、k2的轻弹簧系住一个质量为m的小球，开始时，两弹簧均处于原长，后使小球向左偏离x后放手，可以看到小球将在水平面上作往复振动，试问小球是否作简谐运动？
分析：
为了判断小球的运动性质，需要根据小球的受力情况，找出回复力，确定它能否写成F=-kx的形式。
解析：
以小球为研究对象，竖直方向处于力平衡状态，水平方向受到两根弹簧的弹力作用，设小球位于平衡位置O左方某处时，偏离平衡位置的位移为x，则
左方弹簧受压，对小球的弹力大小为F1=k1x，方向向右。
右方弹簧被拉伸，对小球的弹力大小为F2=k2x方向向右。
小球所受回复力等于两个弹力的合力，其大小为F=F1+F2=(k1+k2)x，方向向右，
令k=k1+k2，上式可写成F=kx
由于小球所受回复力的方向与位移x的方向相反，考虑方向后，上式可表示为F=-kx所以，小球将在两根弹簧的作用下，沿水平面简谐运动。
说明：
由本题可归纳出判断物体是否作简谐运动的一般步骤：确定研究对象（整个物体或某一部分）→分析受力情况→找出回复力→表示成F=-kx的形式（可以先确定F的大小与x的关系，再定性判断方向）。
【达标训练】
1．做简谐运动的质点，先后经过同一点时，下列物理量哪些是不同的（
）
A．速度
B．加速度
C．位移
D．动能
2．某个弹簧振子在水平方向上做简谐运动，下列说法中正确的是（
）
A．该振子的加速度和位移大小成正比，方向相反
B．该振子的加速度和位移大小成正比，方向相同
C．该振子做非匀变速运动
D．该振子做匀变速运动
3．弹簧振子做简谐运动时，下列说法中正确的是（
）
A．若位移为负值，则速度一定为正值
B．振子通过平衡位置时，速度为零，加速度最大
C．振子每次通过平衡位置时，加速度相同，速度也相同
D．振子通过同一位置时，速度不一定相同，但加速度一定相同
4．如图，一水平弹簧振子，O为平衡位置，振子在B、C之间做简谐运动，设向右为正方向，则振子（
）
A．由C向O运动时，位移为正值，速度为正值，加速度为正值
B．由O向B
运动时，位移为正值，速度为正值，加速度为负值
C．由B
向O运动时，位移为负值，速度为正值，加速度为负值
D．由O向C运动时，位移为负值，速度为负值，加速度为正值
5．水平方向做简谐运动的物体偏离平衡位置的位移为X，速度为V，加速度为a，则（
）
A．X与V同向时，物体加速
B．X与V反向时，物体加速
C．V与a同向时，位移变大，
D．V与a反向时，位移变大
6．关于水平方向上做简谐运动的弹簧振子的位移，加速度和速度间的关系，下列说法中正确的是（
）
A．位移减小时，加速度减小，速度增大
B．位移的方向
总是跟加速度的方向
相反，跟速度的方向相同
C．振子的运动方向
指向平衡位置
时，速度的方向
跟位移方向相同
D．振子的运动方向改变时，加速度的方向也改变
7．如图，若水平弹簧振子在B、C间做简谐运动，O点为平衡位置，则（
）
A．振子在经过O
点时速度最大，回复力也最大
B．振子在经过O
点时速度最大，回复力为零
C．振子在由C点向O
点运动的过程中，回复力逐渐减小，
加速度却逐渐增大
D．振子在由O
点向B点运动的过程中，弹性势能逐渐增大，加速度却逐渐减小
8．若做简谐运动的弹簧振子的振幅是A，最大加速度的值为am，则在位移X=A/2处振子的加速度值a=
。
答案
题号
1
2
3
4
5
答案
A
AC
D
BD
BD
题号
6
7
8
答案
A
B
1/2
【反思】
收获
疑问
O
A
A′
x
x
O
B
C
O
B
C