《相似三角形》复习教案(新人教版九年级下)
文档属性
| 名称 | 《相似三角形》复习教案(新人教版九年级下) |
|
|
| 格式 | rar | ||
| 文件大小 | 64.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-22 00:00:00 | ||
图片预览

文档简介
《相似三角形》复习教案
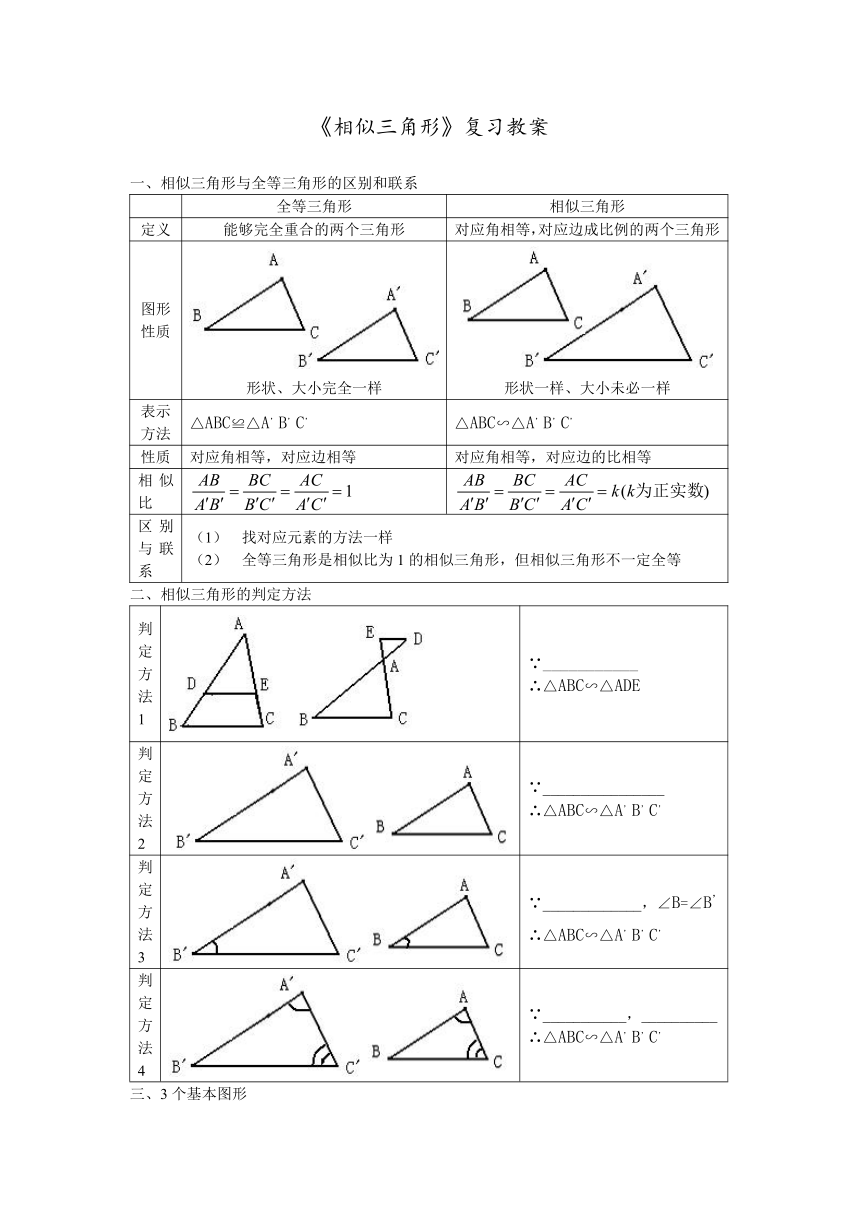
一、相似三角形与全等三角形的区别和联系
全等三角形 相似三角形
定义 能够完全重合的两个三角形 对应角相等,对应边成比例的两个三角形
图形性质 形状、大小完全一样 形状一样、大小未必一样
表示方法 △ABC≌△A,B,C, △ABC∽△A,B,C,
性质 对应角相等,对应边相等 对应角相等,对应边的比相等
相似比
区别与联系 找对应元素的方法一样全等三角形是相似比为1的相似三角形,但相似三角形不一定全等
二、相似三角形的判定方法
判定方法1 ∵___________∴△ABC∽△ADE
判定方法2 ∵________________∴△ABC∽△A,B,C,
判定方法3 ∵_____________,∠B=∠B,∴△ABC∽△A,B,C,
判定方法4 ∵___________,__________∴△ABC∽△A,B,C,
三、3个基本图形
∵_______________∴△APC∽△DPB则PA PB=PC PD
∵_________________∴△APD∽△CPB则PA PB=PC PD
△ACD∽△CBD∽△ABC
四、例题
例1、平行四边形ABCD中,M为对角线AC上一点,BM交AD于N,交CD延长线于E。试问图中有多少对不同的相似三角形?
例2、如图, Rt△ABC, 斜边AC上有一点D(不与点A、C重合), 过D点作直线截△ABC, 使截得的三角形与△ABC相似, 则满足这样条件的直线共有________条。
例3、如图,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是_________。
小练习:
如图,已知⊙O的两条弦AB、CD相交与AB的中点E,且AB=4,DE=CE+3,求CD的长。
例4、已知:如图,AB∥A’B’,BC∥B’C’,求证:△OAC∽△OA’C’。
小练习:
(对例4的图变形:将O点移到△ABC外部)
已知:如图,AB∥A’B’,BC∥B’C’,求证:△OAC∽△OA’C’。
例5、如图,A、B、D、E四点在⊙O上,AE、BD的延长线相交于点C,直径AE为8,OC=12,∠EDC=∠BAO。
(1)求证:;
(2)计算CD CB的值,并指出CB的取值范围。
例6、如图,正方形ABCD中,E、F分别在AB、BC边上,且AE=CF、BG⊥CE于G。试证明DG⊥FG。
例7、在Rt△ABC中,∠C=90O,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F,问当点D在什么位置时,四边形CDEF的面积最大?
P
·
C
O
D
A
B
一、相似三角形与全等三角形的区别和联系
全等三角形 相似三角形
定义 能够完全重合的两个三角形 对应角相等,对应边成比例的两个三角形
图形性质 形状、大小完全一样 形状一样、大小未必一样
表示方法 △ABC≌△A,B,C, △ABC∽△A,B,C,
性质 对应角相等,对应边相等 对应角相等,对应边的比相等
相似比
区别与联系 找对应元素的方法一样全等三角形是相似比为1的相似三角形,但相似三角形不一定全等
二、相似三角形的判定方法
判定方法1 ∵___________∴△ABC∽△ADE
判定方法2 ∵________________∴△ABC∽△A,B,C,
判定方法3 ∵_____________,∠B=∠B,∴△ABC∽△A,B,C,
判定方法4 ∵___________,__________∴△ABC∽△A,B,C,
三、3个基本图形
∵_______________∴△APC∽△DPB则PA PB=PC PD
∵_________________∴△APD∽△CPB则PA PB=PC PD
△ACD∽△CBD∽△ABC
四、例题
例1、平行四边形ABCD中,M为对角线AC上一点,BM交AD于N,交CD延长线于E。试问图中有多少对不同的相似三角形?
例2、如图, Rt△ABC, 斜边AC上有一点D(不与点A、C重合), 过D点作直线截△ABC, 使截得的三角形与△ABC相似, 则满足这样条件的直线共有________条。
例3、如图,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是_________。
小练习:
如图,已知⊙O的两条弦AB、CD相交与AB的中点E,且AB=4,DE=CE+3,求CD的长。
例4、已知:如图,AB∥A’B’,BC∥B’C’,求证:△OAC∽△OA’C’。
小练习:
(对例4的图变形:将O点移到△ABC外部)
已知:如图,AB∥A’B’,BC∥B’C’,求证:△OAC∽△OA’C’。
例5、如图,A、B、D、E四点在⊙O上,AE、BD的延长线相交于点C,直径AE为8,OC=12,∠EDC=∠BAO。
(1)求证:;
(2)计算CD CB的值,并指出CB的取值范围。
例6、如图,正方形ABCD中,E、F分别在AB、BC边上,且AE=CF、BG⊥CE于G。试证明DG⊥FG。
例7、在Rt△ABC中,∠C=90O,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F,问当点D在什么位置时,四边形CDEF的面积最大?
P
·
C
O
D
A
B
