4.1 光的折射定律 同步练习 (含答案解析) (2)
文档属性
| 名称 | 4.1 光的折射定律 同步练习 (含答案解析) (2) |

|
|
| 格式 | zip | ||
| 文件大小 | 179.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-31 07:08:43 | ||
图片预览


文档简介
4.1
光的折射定律
同步练习
1.一条光线从空气射入折射率为的介质中,入射角为45°,在界面上入射光的一部分被反射,另一部分被折射,则反射光线和折射光线的夹角是(
)
A.75°
B.90°
C.105°
D.120°
解析:如图所示,根据折射定律=n,则sinr=,r=30°,反射光线与折射光线的夹角θ=180°-45°-30°=105°,C正确.
答案:C
2.假设地球表面不存在大气层,那么人们观察到的日出时刻与实际存在大气层的情况相比(
)
A.将提前
B.将延后
C.在某些地区将提前,在另一些地区将延后
D.不变
解析:如图所示,假设地球表面不存在大气层,则地球上M处的人只能等到太阳运动到S处才看见日出,而地球表面存在大气层时,太阳运动到S′处,阳光经大气层折射后即射至M点,故M点观察到的日出时刻比不存在大气层时要提前.正确选项为B.
答案:B
3.如图4-1-9中,一玻璃柱体的横截面为半圆形.细的单色光束从空气射向柱体的O点(半圆的圆心),产生反射光束1和折射光束2.已知玻璃折射率为,入射角为45°(相应的折射角为24°).现保持入射光不变,将半圆柱绕O点在图示平面内顺时针转过15°,如图中虚线所示,则(
)
图4-1-9
A.光束1转过15°
B.光束1转过30°
C.光束2转过的角度小于15°
D.光束2转过的角度大于15°
解析:转动前,光束1(反射光)与入射光线间的夹角为A=45°×2=90°,光束2(折射光)与入射光线间的夹角为B=45°+(180°-24°)=201°.
转动后,反射光与入射光的夹角A′=60°×2=120°,
据折射定律,,得r=30°,则折射光与入射光间的夹角为B′=60°+(180°-30°)=210°.
因为ΔA=A′-A=30°,ΔB=B′-B=9°,故B、C项正确.
答案:BC
4.测定玻璃的折射率时,为了减少实验误差,应该注意的是(
)
A.玻璃砖的宽度宜大些
B.入射角应尽量小些
C.大头针应垂直地插在纸面上
D.大头针P1和P2及P3和P4之间的距离适当大些
解析:该实验误差来源主要是折射角的测量值,为使折射角的测量值尽量准确,(1)要使入射角大些;(2)玻璃砖的宽度大些;(3)大头针的间距要大些;(4)大头针要竖直插,故A、C、D正确.
答案:ACD
5.某同学由于没有量角器,在完成了光路图以后,以O点为圆心,10.00
cm
长为半径画圆,分别交线段OA于A点,交O和O′连线延长线于C点,过A点作法线NN′的垂线,AB交NN′于B点,过C点作法线NN′的垂线CD交NN′于D点,如图4-1-10所示,用刻度尺量得OB=8.00
cm,CD=4.00
cm,由此可得出玻璃的折射率n=__________.
图4-1-10
解析:由光路图以及几何关系可知:
n==1.5.
答案:1.5
6.有人在游泳池边上竖直向下观察池水的深度,看到池水的深度约为h,已知水的折射率n=4/3,那么,水的实际深度约为多少
解析:设水池的实际深度为H,水的视深为h,从正上方沿竖直向下的方向观察池底S时,由于光的折射现象,其视深位置在S′处,观察光路如图所示.
由几何关系和折射定律可知:
sini=nsinr
O1O2=htani=Htanr
考虑到从正上方观察时,角度i和r均很小,所以有:sini≈tani,sinr≈tanr因此H=nh=h.
答案:h
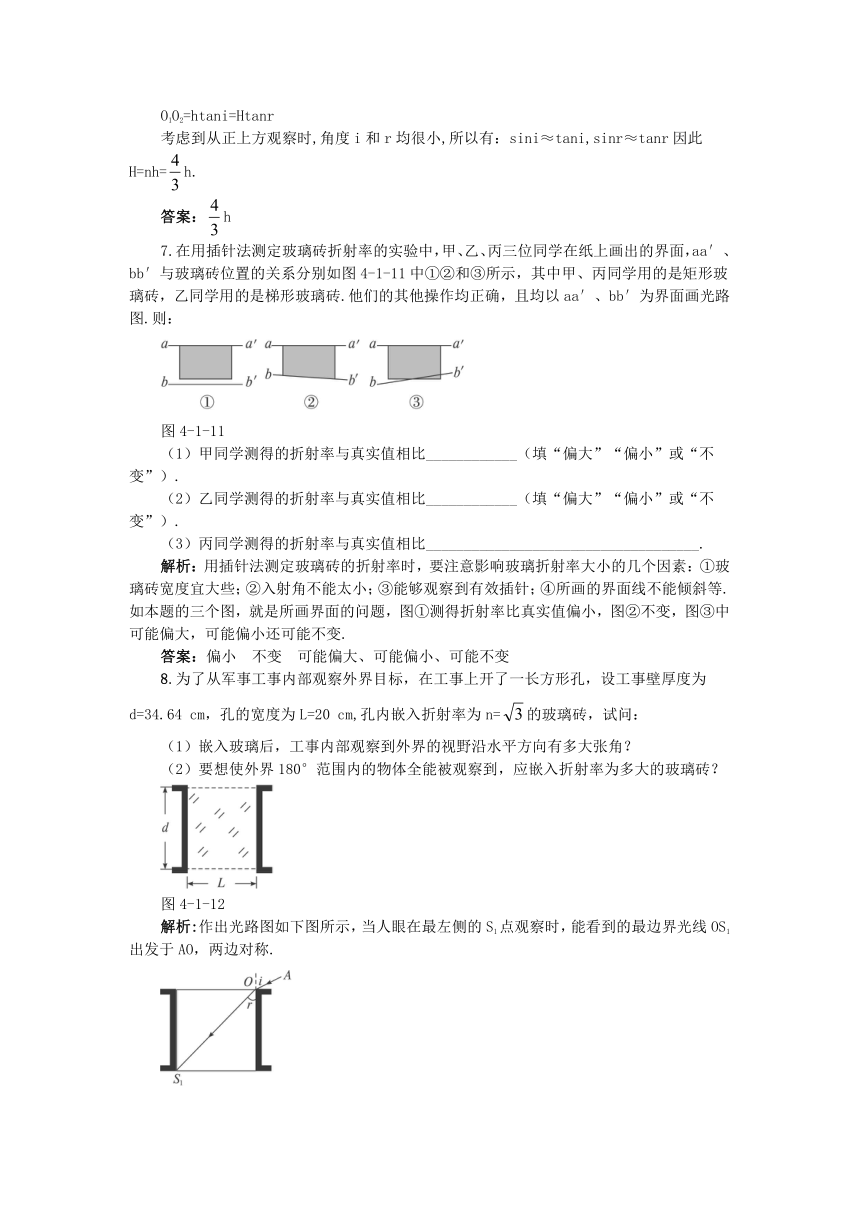
7.在用插针法测定玻璃砖折射率的实验中,甲、乙、丙三位同学在纸上画出的界面,aa′、bb′与玻璃砖位置的关系分别如图4-1-11中①②和③所示,其中甲、丙同学用的是矩形玻璃砖,乙同学用的是梯形玻璃砖.他们的其他操作均正确,且均以aa′、bb′为界面画光路图.则:
图4-1-11
(1)甲同学测得的折射率与真实值相比____________(填“偏大”“偏小”或“不变”).
(2)乙同学测得的折射率与真实值相比____________(填“偏大”“偏小”或“不变”).
(3)丙同学测得的折射率与真实值相比____________________________________.
解析:用插针法测定玻璃砖的折射率时,要注意影响玻璃折射率大小的几个因素:①玻璃砖宽度宜大些;②入射角不能太小;③能够观察到有效插针;④所画的界面线不能倾斜等.如本题的三个图,就是所画界面的问题,图①测得折射率比真实值偏小,图②不变,图③中可能偏大,可能偏小还可能不变.
答案:偏小
不变
可能偏大、可能偏小、可能不变
8.为了从军事工事内部观察外界目标,在工事上开了一长方形孔,设工事壁厚度为d=34.64
cm,孔的宽度为L=20
cm,孔内嵌入折射率为n=的玻璃砖,试问:
(1)嵌入玻璃后,工事内部观察到外界的视野沿水平方向有多大张角?
(2)要想使外界180°范围内的物体全能被观察到,应嵌入折射率为多大的玻璃砖?
图4-1-12
解析:作出光路图如下图所示,当人眼在最左侧的S1点观察时,能看到的最边界光线OS1出发于AO,两边对称.
(1)如图所示,AO为人在最左侧的S1点观察到的边界光线,由几何关系得:tanr==,所以r=30°
由折射定律,所以i=60°
同理,眼睛位于最右侧时,也能看到左侧同样角度内的景物,故观察视野的最大张角为
60°×2=120°.
(2)要观察到180°范围内景物,则i=90°时,r=30°
所以n===2
应嵌入折射率为2的玻璃砖.
答案:(1)120°
(2)2
9.如图4-1-13所示为一透明的圆柱体的横截面,其半径为R,折射率为,AB是一条直径,若有一束平行光沿AB方向射向圆柱体,折射后经过B点的入射光线离AB的距离为多少?
图4-1-13
解析:可先作出光路图,用折射定律结合几何知识求出.
如图所示,设折射后经过B点的入射光线的射入点为C,连接BC,则BC为其折射光线,OC为法线,若折射角为θ,由几何知识可知入射角为2θ,根据折射定律有
,即θ=30°.
则入射光线离AB的距离
CD=Rsin2θ=R.
答案:R
10.如图4-1-14所示,一个人发现水中S处有一溺水者,溺水者离岸的距离SB=10
m,而发现者在A处,距B点的距离为20
m,此人在岸上跑动的速度为5
m/s,而在水中的速度为1
m/s,发现者为尽快到达溺水者处,他应在何处下水
图4-1-14
解析:这是一个运动学问题,但与光的折射现象有相似之处,发现者为了尽快到达S处,假设他从P处下水.(BP=x),就相当于入射光的入射角为
i=90°,sini/sinr==5
因为sinr=
所以=5
解得x=m=2.04
m.即发现者应从距B点2.04
m处下水.
答案:2.04
m
11.一长直杆长1.5
m,垂直立于底部平坦、水面平静无波的游泳池中,露出水面部分高0.3
m,当阳光以与水面成37°的夹角入射时,杆在游泳池底部所成的影长为多少 已知水的折射率n=.
解析:依题意作图如图所示,依据折射定律
n=,得sinr=,r=37°,
影长s=0.3×tan53°
m+1.2×tan37°
m=0.3×m+1.2×m=1.3
m.
答案:1.3
m
12.在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S发出的光线SA以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如图4-1-15所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃上表面的垂直距离L应是多少
图4-1-15
解析:设光线在玻璃中的折射角为r,则光线从S到玻璃板上表面的传播距离为,光线从S到玻璃板上表面的传播时间为,其中c是真空中的光速,光在玻璃板中的传播距离为,光在玻璃中的传播时间为,由折射定律:sinθ=nsinr
根据题意得:=联立解得:
L=d.
答案:
d
13.光线以60°的入射角从空气射入玻璃中,折射光线与反射光线恰好垂直.(真空中的光速c=3.0×108
m/s)
(1)画出折射光路图;
(2)求出玻璃的折射率和光在玻璃中的传播速度;
(3)当入射角变为45°时,折射角等于多大;
(4)当入射角增大或减小时,玻璃的折射率是否变化 说明理由.
解答:先画出玻璃与空气的界面.再过入射点作出界面的垂线即为法线,然后根据光的反射定律和折射定律作出入射光线、反射光线和折射光线;求出折射角r后,据n=求出n,当入射角变化时,这一比值保持不变即玻璃的折射率并不改变,据n=求出v.
(1)由题意知入射角i=60°,反射角β=60°,折射角r=180°-60°-90°=30°,折射光路如图所示.
(2)n==,
据n=得v=m/s
v=1.7×108
m/s.
(3)据n=得sinr=,
代sini=sin45°=及n=入上式,可求得:
sinr=,所以r=arcsin.
(4)折射率不会变化,折射率由介质和入射光的频率决定,而跟入射角的大小无关.
光的折射定律
同步练习
1.一条光线从空气射入折射率为的介质中,入射角为45°,在界面上入射光的一部分被反射,另一部分被折射,则反射光线和折射光线的夹角是(
)
A.75°
B.90°
C.105°
D.120°
解析:如图所示,根据折射定律=n,则sinr=,r=30°,反射光线与折射光线的夹角θ=180°-45°-30°=105°,C正确.
答案:C
2.假设地球表面不存在大气层,那么人们观察到的日出时刻与实际存在大气层的情况相比(
)
A.将提前
B.将延后
C.在某些地区将提前,在另一些地区将延后
D.不变
解析:如图所示,假设地球表面不存在大气层,则地球上M处的人只能等到太阳运动到S处才看见日出,而地球表面存在大气层时,太阳运动到S′处,阳光经大气层折射后即射至M点,故M点观察到的日出时刻比不存在大气层时要提前.正确选项为B.
答案:B
3.如图4-1-9中,一玻璃柱体的横截面为半圆形.细的单色光束从空气射向柱体的O点(半圆的圆心),产生反射光束1和折射光束2.已知玻璃折射率为,入射角为45°(相应的折射角为24°).现保持入射光不变,将半圆柱绕O点在图示平面内顺时针转过15°,如图中虚线所示,则(
)
图4-1-9
A.光束1转过15°
B.光束1转过30°
C.光束2转过的角度小于15°
D.光束2转过的角度大于15°
解析:转动前,光束1(反射光)与入射光线间的夹角为A=45°×2=90°,光束2(折射光)与入射光线间的夹角为B=45°+(180°-24°)=201°.
转动后,反射光与入射光的夹角A′=60°×2=120°,
据折射定律,,得r=30°,则折射光与入射光间的夹角为B′=60°+(180°-30°)=210°.
因为ΔA=A′-A=30°,ΔB=B′-B=9°,故B、C项正确.
答案:BC
4.测定玻璃的折射率时,为了减少实验误差,应该注意的是(
)
A.玻璃砖的宽度宜大些
B.入射角应尽量小些
C.大头针应垂直地插在纸面上
D.大头针P1和P2及P3和P4之间的距离适当大些
解析:该实验误差来源主要是折射角的测量值,为使折射角的测量值尽量准确,(1)要使入射角大些;(2)玻璃砖的宽度大些;(3)大头针的间距要大些;(4)大头针要竖直插,故A、C、D正确.
答案:ACD
5.某同学由于没有量角器,在完成了光路图以后,以O点为圆心,10.00
cm
长为半径画圆,分别交线段OA于A点,交O和O′连线延长线于C点,过A点作法线NN′的垂线,AB交NN′于B点,过C点作法线NN′的垂线CD交NN′于D点,如图4-1-10所示,用刻度尺量得OB=8.00
cm,CD=4.00
cm,由此可得出玻璃的折射率n=__________.
图4-1-10
解析:由光路图以及几何关系可知:
n==1.5.
答案:1.5
6.有人在游泳池边上竖直向下观察池水的深度,看到池水的深度约为h,已知水的折射率n=4/3,那么,水的实际深度约为多少
解析:设水池的实际深度为H,水的视深为h,从正上方沿竖直向下的方向观察池底S时,由于光的折射现象,其视深位置在S′处,观察光路如图所示.
由几何关系和折射定律可知:
sini=nsinr
O1O2=htani=Htanr
考虑到从正上方观察时,角度i和r均很小,所以有:sini≈tani,sinr≈tanr因此H=nh=h.
答案:h
7.在用插针法测定玻璃砖折射率的实验中,甲、乙、丙三位同学在纸上画出的界面,aa′、bb′与玻璃砖位置的关系分别如图4-1-11中①②和③所示,其中甲、丙同学用的是矩形玻璃砖,乙同学用的是梯形玻璃砖.他们的其他操作均正确,且均以aa′、bb′为界面画光路图.则:
图4-1-11
(1)甲同学测得的折射率与真实值相比____________(填“偏大”“偏小”或“不变”).
(2)乙同学测得的折射率与真实值相比____________(填“偏大”“偏小”或“不变”).
(3)丙同学测得的折射率与真实值相比____________________________________.
解析:用插针法测定玻璃砖的折射率时,要注意影响玻璃折射率大小的几个因素:①玻璃砖宽度宜大些;②入射角不能太小;③能够观察到有效插针;④所画的界面线不能倾斜等.如本题的三个图,就是所画界面的问题,图①测得折射率比真实值偏小,图②不变,图③中可能偏大,可能偏小还可能不变.
答案:偏小
不变
可能偏大、可能偏小、可能不变
8.为了从军事工事内部观察外界目标,在工事上开了一长方形孔,设工事壁厚度为d=34.64
cm,孔的宽度为L=20
cm,孔内嵌入折射率为n=的玻璃砖,试问:
(1)嵌入玻璃后,工事内部观察到外界的视野沿水平方向有多大张角?
(2)要想使外界180°范围内的物体全能被观察到,应嵌入折射率为多大的玻璃砖?
图4-1-12
解析:作出光路图如下图所示,当人眼在最左侧的S1点观察时,能看到的最边界光线OS1出发于AO,两边对称.
(1)如图所示,AO为人在最左侧的S1点观察到的边界光线,由几何关系得:tanr==,所以r=30°
由折射定律,所以i=60°
同理,眼睛位于最右侧时,也能看到左侧同样角度内的景物,故观察视野的最大张角为
60°×2=120°.
(2)要观察到180°范围内景物,则i=90°时,r=30°
所以n===2
应嵌入折射率为2的玻璃砖.
答案:(1)120°
(2)2
9.如图4-1-13所示为一透明的圆柱体的横截面,其半径为R,折射率为,AB是一条直径,若有一束平行光沿AB方向射向圆柱体,折射后经过B点的入射光线离AB的距离为多少?
图4-1-13
解析:可先作出光路图,用折射定律结合几何知识求出.
如图所示,设折射后经过B点的入射光线的射入点为C,连接BC,则BC为其折射光线,OC为法线,若折射角为θ,由几何知识可知入射角为2θ,根据折射定律有
,即θ=30°.
则入射光线离AB的距离
CD=Rsin2θ=R.
答案:R
10.如图4-1-14所示,一个人发现水中S处有一溺水者,溺水者离岸的距离SB=10
m,而发现者在A处,距B点的距离为20
m,此人在岸上跑动的速度为5
m/s,而在水中的速度为1
m/s,发现者为尽快到达溺水者处,他应在何处下水
图4-1-14
解析:这是一个运动学问题,但与光的折射现象有相似之处,发现者为了尽快到达S处,假设他从P处下水.(BP=x),就相当于入射光的入射角为
i=90°,sini/sinr==5
因为sinr=
所以=5
解得x=m=2.04
m.即发现者应从距B点2.04
m处下水.
答案:2.04
m
11.一长直杆长1.5
m,垂直立于底部平坦、水面平静无波的游泳池中,露出水面部分高0.3
m,当阳光以与水面成37°的夹角入射时,杆在游泳池底部所成的影长为多少 已知水的折射率n=.
解析:依题意作图如图所示,依据折射定律
n=,得sinr=,r=37°,
影长s=0.3×tan53°
m+1.2×tan37°
m=0.3×m+1.2×m=1.3
m.
答案:1.3
m
12.在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S发出的光线SA以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如图4-1-15所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃上表面的垂直距离L应是多少
图4-1-15
解析:设光线在玻璃中的折射角为r,则光线从S到玻璃板上表面的传播距离为,光线从S到玻璃板上表面的传播时间为,其中c是真空中的光速,光在玻璃板中的传播距离为,光在玻璃中的传播时间为,由折射定律:sinθ=nsinr
根据题意得:=联立解得:
L=d.
答案:
d
13.光线以60°的入射角从空气射入玻璃中,折射光线与反射光线恰好垂直.(真空中的光速c=3.0×108
m/s)
(1)画出折射光路图;
(2)求出玻璃的折射率和光在玻璃中的传播速度;
(3)当入射角变为45°时,折射角等于多大;
(4)当入射角增大或减小时,玻璃的折射率是否变化 说明理由.
解答:先画出玻璃与空气的界面.再过入射点作出界面的垂线即为法线,然后根据光的反射定律和折射定律作出入射光线、反射光线和折射光线;求出折射角r后,据n=求出n,当入射角变化时,这一比值保持不变即玻璃的折射率并不改变,据n=求出v.
(1)由题意知入射角i=60°,反射角β=60°,折射角r=180°-60°-90°=30°,折射光路如图所示.
(2)n==,
据n=得v=m/s
v=1.7×108
m/s.
(3)据n=得sinr=,
代sini=sin45°=及n=入上式,可求得:
sinr=,所以r=arcsin.
(4)折射率不会变化,折射率由介质和入射光的频率决定,而跟入射角的大小无关.
同课章节目录
- 第1章 机械振动
- 导 入 从我国古代的“鱼洗”说起
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 生活中的振动
- 第2章 机械波
- 导 入 身边的波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第3章 电磁波
- 导 入 无处不在的电磁波
- 第1节 电磁波的产生
- 第2节 电磁波的发射、传播和接收
- 第3节 电磁波的应用及防护
- 专题探究 振动与波的实验与调研
- 第4章 光的折射与全反射
- 导 入 美妙的彩虹
- 第1节 光的折射定律
- 第2节 光的全反射
- 第3节 光导纤维及其应用
- 第5章 光的干涉 衍射 偏振
- 导 入 从五彩斑斓的肥皂泡说起
- 第1节 光的干涉
- 第2节 光的衍射
- 第3节 光的偏振
- 第4节 激光与全息照相
- 专题探究 光学部分的实验与调研
- 第6章 相对论与天体物理
- 导 入 从双生子佯谬谈起
- 第1节 牛顿眼中的世界
- 第2节 爱因斯坦眼中的世界
- 第3节 广义相对论初步
- 第4节 探索宇宙
