第1章 机械振动(综合复习) 教案 (3)
文档属性
| 名称 | 第1章 机械振动(综合复习) 教案 (3) |

|
|
| 格式 | zip | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-31 13:19:19 | ||
图片预览


文档简介
第1章
机械振动(综合复习)
教案3(鲁教版选修3-4)
教学目标:
1.知识目标
通过例题的讲解,使学生对本章的基本概念和基本规律有进一步地理解,并能熟练应用本章知识分析解决物理问题。
2.能力目标
在熟练掌握基本概念、基本规律的基础上,能够分析和解决一些实际问题。
3.物理方法教育目标
通过复习,培养学生归纳知识和进一步运用知识的能力,学习一定的研究问题的科学方法。
复习重点:
对物理概念的深刻含义、对物理概念的综合性运用
教学方法:
复习提问,讲练结合,学案导学
教学过程
一、单
摆
(1)单摆:一条不可伸长的、忽略质量的细线,一端固定,另一端拴一质点,这样构成的装置叫单摆.
这是一种理想化的模型,实际悬线(杆)下接小球的装置都可作为单摆.
(2)单摆振动可看作简谐运动的条件是最大偏角α<5°.
(3)摆球做简谐运动
回复力:是重力在切线方向的分力F回=G1;
重力的另一分力G2和摆线的拉力合力提供向心力;F-G2=mv2/l
在最大位移处v=0,F=G2.
(4)周期公式:
式中L为小球摆动的圆孤半径即摆长,量取时应从圆心量到球心.g为当地重力加速度(受力复杂时有“等效重力加速度”之说).
(5)单摆的等时性:在小振幅摆动时,单摆的振动周期跟振幅和振子的质量都没关系.
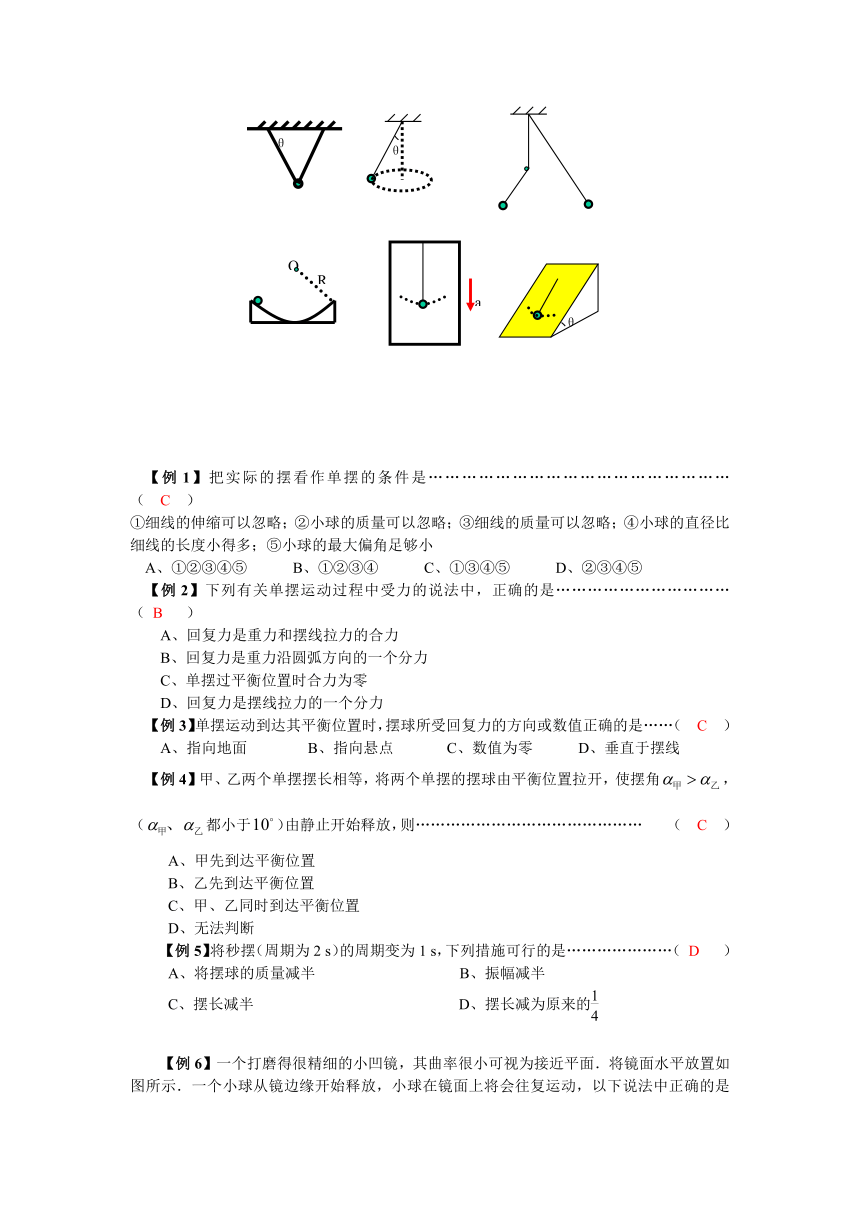
(6)几种单摆模型
【例1】把实际的摆看作单摆的条件是………………………………………………
(
C
)
①细线的伸缩可以忽略;②小球的质量可以忽略;③细线的质量可以忽略;④小球的直径比细线的长度小得多;⑤小球的最大偏角足够小
A、①②③④⑤
B、①②③④
C、①③④⑤
D、②③④⑤
【例2】下列有关单摆运动过程中受力的说法中,正确的是……………………………(
B
)
A、回复力是重力和摆线拉力的合力
B、回复力是重力沿圆弧方向的一个分力
C、单摆过平衡位置时合力为零
D、回复力是摆线拉力的一个分力
【例3】单摆运动到达其平衡位置时,摆球所受回复力的方向或数值正确的是……(
C
)
A、指向地面
B、指向悬点
C、数值为零
D、垂直于摆线
【例4】甲、乙两个单摆摆长相等,将两个单摆的摆球由平衡位置拉开,使摆角,(都小于)由静止开始释放,则………………………………………
(
C
)
A、甲先到达平衡位置
B、乙先到达平衡位置
C、甲、乙同时到达平衡位置
D、无法判断
【例5】将秒摆(周期为2
s)的周期变为1
s,下列措施可行的是…………………(
D
)
A、将摆球的质量减半
B、振幅减半
C、摆长减半
D、摆长减为原来的
【例6】一个打磨得很精细的小凹镜,其曲率很小可视为面.将镜面水平放置如图所示.一个小球从镜边缘开始释放,小球在镜面上将会往复运动,以下说法中正确的是(
C
)
A.小球质量越大,往复运动的周期越长
B.释放点离最低点距离越大,周期越短
C.凹镜曲率半径越大,周期越长
D.周期应由小球质量、释放点离平衡位置的距离,以及曲率半径共同决定
【例7】.关于小孩子荡秋千,有下列四种说法:
①质量大一些的孩子荡秋千,它摆动的频率会更大些
②孩子在秋千达到最低点处有失重的感觉
③拉绳被磨损了的秋千,绳子最容易在最低点断开
④自己荡秋千想荡高一些,必须在两侧最高点提高重心,增加势能
(
B
)
上述说法中正确的是
A.①②
B.③④
C.②④
D.②③
【例8】细长轻绳下端拴一小球构成单摆,在悬挂点正下方摆长处有一个能挡住摆线的钉子A,如图所示.现将单摆向左方拉开一个小角度,然后无初速地释放,对于以后的运动,下列说法中正确的是
(
AB
)
A.摆球往返运动一次的周期比无钉子时的单摆周期小
B.摆球在左、右两侧上升的最大高度一样
C.摆球在平衡位置左右两侧走过的最大弧长相等
D.摆线在平衡位置右侧的最大摆角是左侧的两倍
【例9】一只单摆在第一行星表面上的周期为T1,在第二行星表面上的周期为T2,若这两个行星的质量之比M1∶M2=4∶1,半径之比R1∶R2=2∶1,则
(
A
)
A.T1∶T2=1∶1
B.T1∶T2=4∶1
C.T1∶T2=2∶1
D.T1∶T2=2∶1
【例10】(1)某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.50cm;用50分度的游标卡尺(测量值可准确到0.02mm)测得小球的读数如图所示,则摆球直径为
cm;然后用秒表记录了单摆振动50次所用的时间为99.9s.则
①该摆摆长为_______cm,周期为
s
②(单选题)如果他测得的g值偏小,可能的原因是
[
]
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时,秒表过迟按下
D.实验中误将49次全振动数为50次
(2.00,98.50,2.00
,A)
(2)在一次用单摆测定加速度的实验中,图A的O点是摆线的悬挂点,a、b点分别是球的上沿和球心,摆长L=
m.
图B为测量周期用的秒表,长针转一圈的时间为30s,表盘上部的小圆共15大格,每一大格为lmin,该单摆摆动n=50次时,长、短针位置如图中所示,所用时间t=
s.
用以上直接测量的物理量的英文符号表示重力加速度的计算式为
g=
(不必代入具体数值).
为了提高测量精度,需多次改变L的值并测得相应的T值.现测得的六组数据标示在以L为横坐标、T为纵坐标的坐标纸上,即图中用“”表示的点。根据图中的数据点作出T2与L的关系图线.
答案.
0.9906
,100.40;
;略
二、受迫振动和振动的能量
(1)对于给定的振动系统,振动的动能由振动的速度决定,振动的势能由振动的位移决定,振动的能量就是振动系统在某个状态下的动能与势能之和.
(2)振动系统的机械能大小由振幅大小决定,同一系统振幅越大,机械能就越大.若无能量损失,简谐运动过程中机械能守恒,为等幅振动.
2.阻尼振动与无阻尼振动
振幅逐渐减小的振动叫阻尼振动.
振幅不变的振动为等幅振动,也叫无阻尼振动.
3.受迫振动
振动系统在周期性驱动力作用下的振动叫受迫振动.
受迫振动稳定时,系统振动的频率等于驱动力的频率,跟系统的固有频率无关.
4.共振
当驱动力的频率等于振动系统的固有频率时,振动物体的振幅最大的现象叫做共振.
共振曲线如图所示
【例11】工厂里,有一台机器正在运转,当其飞轮转得很快的时候,机器的振动并不强烈,切断电源,飞轮逐渐慢下来,到某一时刻机器发生强烈的振动,此后飞轮转得更慢,机器的振动又转动减弱。这种现象说明(
D
)
A.纯属偶然现象,并无规律
B.在某一时刻,飞轮的惯性最大
C.在某一时刻,飞轮转动的频率最大
D.在某一时刻,飞轮转动的频率与机身的固有频率相等
【例12】如图所示,在曲轴上悬挂一弹簧振子,转动摇把,曲轴可以带动弹簧振子上下振动。开始时不转动摇把,让振子自由上下振动,测得其频率为2HZ;然后以60r/min的转速匀速转动摇把,当振子振动稳定时,它的振动周期为(
C
)
A.0.25s
B.0.5
s
C.1
s
D.2s
【例13】单摆在振动过程中,摆动幅度越来越小这是因为:(
D
)
A.能量正在逐渐消灭
B.动能正在转化为势能
C.机械能守恒
D.总能量守恒,减少的动能转化为内能
【例14】任何物体都有一定的固有频率.如果把人作为一个振动系统,在水平方向的固有频率约为3
Hz~6
Hz,在竖直方向的固有频率约为4
Hz~8
Hz.拖拉机、风镐、风铲、铆钉机等的操作工在工作时将做________振动,这时若操作工的固有频率与振源振动的频率________,就会对操作工的健康造成伤害.为保证操作工的安全与健康,有关部门作出规定:用于操作的各类振动机械的频率必须大于20
Hz,这是为了防止________所造成的伤害.
答案:受迫
接近或相等
共振
【例15】如图所示,一轻弹簧的左端固定在竖直墙上,右端与质量为M的滑块相连,组成弹簧振子,在光滑的水平面上做简谐运动.当滑块运动到右侧最大位移处时,在滑块上轻轻放上一木块组成新振子,继续做简谐运动.新振子的运动过程与原振子的运动过程相比(
AC
)
A.新振子的最大速度比原振子的最大速度小
B.新振子的最大动能比原振子的最大动能小
C.新振子的振动周期比原振子的振动周期大
D.新振子的振幅比原振子的振幅小
【例16】右图为一单摆的共振曲线,则该单摆的摆长约为多少?共振时单摆的振幅多大?(g取10m/s2)
解:由图可知,单摆在f驱=0.5Hz时振动最剧烈,表明此时发生了共振,振幅为10cm。
由,得:L===1.01m
【例17】如图1所示,三角架质量为M,沿其中轴线用两根轻弹簧拴一质量为m的小球,原来三角架静止在水平面上.现使小球做上下振动,已知三角架对水平面的压力最小为零,求:
(1)此时小球的瞬时加速度;
(2)若上、下两弹簧的劲度系数均为k,则小球做简谐运动的振幅为多少
答案:
(1)
g,方向竖直向下
(2)
解析:(1)当小球上下振动过程中,三角架对水平面的压力最小为零,则上下两根弹簧对三角架的作用力大小为Mg,方向向下,小球此时受弹簧的弹力大小为Mg,方向向上,故小球所受合力为(m+M)g,方向向下,小球此时运动到上面最高点即位移大小等于振幅处.根据牛顿第二定律,小球的瞬时加速度的最大值为:am=,加速度的方向为竖直向下.
(2)小球由平衡位置上升至最高点时,上面的弹簧(相当于压缩x)对小球会产生向下的弹力kx,下面的弹簧(相当于伸长x)会对小球产生向下的弹力kx,两根弹簧对小球的作用力为2kx,故最大回复力大小F回=2kA,而最高时F回=(M+m)g,故A=.
【例18】如图,A、B两单摆摆长分别为
、,两球静止时刚好接触,且重心等高、质量相等。今把A球从平衡位置向右拉开一个微小角度,然后无初速释放,于是AB将发生一系列弹性正碰,设碰撞后两球速度互换,碰撞时间不计.则释放A球后20s内两球碰撞多少次?
解:先求出AB摆长的单摆周期:
A释放后经与B发生碰撞,碰后速度交换,A静止,B球向左摆动,再经又摆回与A发生碰撞,碰后B静止,A向右运动,再经回到最右边。可见每经过,A、B发生两次碰撞,A又回到释放初的最右位置。所以有:
表明经过了13个碰撞周期,碰了26次,而0。5s正好是TA/4,所以第20s末A刚好回到平衡位置,第27次碰撞正在发生.
R
O
a
θ
θ
θ
机械振动(综合复习)
教案3(鲁教版选修3-4)
教学目标:
1.知识目标
通过例题的讲解,使学生对本章的基本概念和基本规律有进一步地理解,并能熟练应用本章知识分析解决物理问题。
2.能力目标
在熟练掌握基本概念、基本规律的基础上,能够分析和解决一些实际问题。
3.物理方法教育目标
通过复习,培养学生归纳知识和进一步运用知识的能力,学习一定的研究问题的科学方法。
复习重点:
对物理概念的深刻含义、对物理概念的综合性运用
教学方法:
复习提问,讲练结合,学案导学
教学过程
一、单
摆
(1)单摆:一条不可伸长的、忽略质量的细线,一端固定,另一端拴一质点,这样构成的装置叫单摆.
这是一种理想化的模型,实际悬线(杆)下接小球的装置都可作为单摆.
(2)单摆振动可看作简谐运动的条件是最大偏角α<5°.
(3)摆球做简谐运动
回复力:是重力在切线方向的分力F回=G1;
重力的另一分力G2和摆线的拉力合力提供向心力;F-G2=mv2/l
在最大位移处v=0,F=G2.
(4)周期公式:
式中L为小球摆动的圆孤半径即摆长,量取时应从圆心量到球心.g为当地重力加速度(受力复杂时有“等效重力加速度”之说).
(5)单摆的等时性:在小振幅摆动时,单摆的振动周期跟振幅和振子的质量都没关系.
(6)几种单摆模型
【例1】把实际的摆看作单摆的条件是………………………………………………
(
C
)
①细线的伸缩可以忽略;②小球的质量可以忽略;③细线的质量可以忽略;④小球的直径比细线的长度小得多;⑤小球的最大偏角足够小
A、①②③④⑤
B、①②③④
C、①③④⑤
D、②③④⑤
【例2】下列有关单摆运动过程中受力的说法中,正确的是……………………………(
B
)
A、回复力是重力和摆线拉力的合力
B、回复力是重力沿圆弧方向的一个分力
C、单摆过平衡位置时合力为零
D、回复力是摆线拉力的一个分力
【例3】单摆运动到达其平衡位置时,摆球所受回复力的方向或数值正确的是……(
C
)
A、指向地面
B、指向悬点
C、数值为零
D、垂直于摆线
【例4】甲、乙两个单摆摆长相等,将两个单摆的摆球由平衡位置拉开,使摆角,(都小于)由静止开始释放,则………………………………………
(
C
)
A、甲先到达平衡位置
B、乙先到达平衡位置
C、甲、乙同时到达平衡位置
D、无法判断
【例5】将秒摆(周期为2
s)的周期变为1
s,下列措施可行的是…………………(
D
)
A、将摆球的质量减半
B、振幅减半
C、摆长减半
D、摆长减为原来的
【例6】一个打磨得很精细的小凹镜,其曲率很小可视为面.将镜面水平放置如图所示.一个小球从镜边缘开始释放,小球在镜面上将会往复运动,以下说法中正确的是(
C
)
A.小球质量越大,往复运动的周期越长
B.释放点离最低点距离越大,周期越短
C.凹镜曲率半径越大,周期越长
D.周期应由小球质量、释放点离平衡位置的距离,以及曲率半径共同决定
【例7】.关于小孩子荡秋千,有下列四种说法:
①质量大一些的孩子荡秋千,它摆动的频率会更大些
②孩子在秋千达到最低点处有失重的感觉
③拉绳被磨损了的秋千,绳子最容易在最低点断开
④自己荡秋千想荡高一些,必须在两侧最高点提高重心,增加势能
(
B
)
上述说法中正确的是
A.①②
B.③④
C.②④
D.②③
【例8】细长轻绳下端拴一小球构成单摆,在悬挂点正下方摆长处有一个能挡住摆线的钉子A,如图所示.现将单摆向左方拉开一个小角度,然后无初速地释放,对于以后的运动,下列说法中正确的是
(
AB
)
A.摆球往返运动一次的周期比无钉子时的单摆周期小
B.摆球在左、右两侧上升的最大高度一样
C.摆球在平衡位置左右两侧走过的最大弧长相等
D.摆线在平衡位置右侧的最大摆角是左侧的两倍
【例9】一只单摆在第一行星表面上的周期为T1,在第二行星表面上的周期为T2,若这两个行星的质量之比M1∶M2=4∶1,半径之比R1∶R2=2∶1,则
(
A
)
A.T1∶T2=1∶1
B.T1∶T2=4∶1
C.T1∶T2=2∶1
D.T1∶T2=2∶1
【例10】(1)某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.50cm;用50分度的游标卡尺(测量值可准确到0.02mm)测得小球的读数如图所示,则摆球直径为
cm;然后用秒表记录了单摆振动50次所用的时间为99.9s.则
①该摆摆长为_______cm,周期为
s
②(单选题)如果他测得的g值偏小,可能的原因是
[
]
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时,秒表过迟按下
D.实验中误将49次全振动数为50次
(2.00,98.50,2.00
,A)
(2)在一次用单摆测定加速度的实验中,图A的O点是摆线的悬挂点,a、b点分别是球的上沿和球心,摆长L=
m.
图B为测量周期用的秒表,长针转一圈的时间为30s,表盘上部的小圆共15大格,每一大格为lmin,该单摆摆动n=50次时,长、短针位置如图中所示,所用时间t=
s.
用以上直接测量的物理量的英文符号表示重力加速度的计算式为
g=
(不必代入具体数值).
为了提高测量精度,需多次改变L的值并测得相应的T值.现测得的六组数据标示在以L为横坐标、T为纵坐标的坐标纸上,即图中用“”表示的点。根据图中的数据点作出T2与L的关系图线.
答案.
0.9906
,100.40;
;略
二、受迫振动和振动的能量
(1)对于给定的振动系统,振动的动能由振动的速度决定,振动的势能由振动的位移决定,振动的能量就是振动系统在某个状态下的动能与势能之和.
(2)振动系统的机械能大小由振幅大小决定,同一系统振幅越大,机械能就越大.若无能量损失,简谐运动过程中机械能守恒,为等幅振动.
2.阻尼振动与无阻尼振动
振幅逐渐减小的振动叫阻尼振动.
振幅不变的振动为等幅振动,也叫无阻尼振动.
3.受迫振动
振动系统在周期性驱动力作用下的振动叫受迫振动.
受迫振动稳定时,系统振动的频率等于驱动力的频率,跟系统的固有频率无关.
4.共振
当驱动力的频率等于振动系统的固有频率时,振动物体的振幅最大的现象叫做共振.
共振曲线如图所示
【例11】工厂里,有一台机器正在运转,当其飞轮转得很快的时候,机器的振动并不强烈,切断电源,飞轮逐渐慢下来,到某一时刻机器发生强烈的振动,此后飞轮转得更慢,机器的振动又转动减弱。这种现象说明(
D
)
A.纯属偶然现象,并无规律
B.在某一时刻,飞轮的惯性最大
C.在某一时刻,飞轮转动的频率最大
D.在某一时刻,飞轮转动的频率与机身的固有频率相等
【例12】如图所示,在曲轴上悬挂一弹簧振子,转动摇把,曲轴可以带动弹簧振子上下振动。开始时不转动摇把,让振子自由上下振动,测得其频率为2HZ;然后以60r/min的转速匀速转动摇把,当振子振动稳定时,它的振动周期为(
C
)
A.0.25s
B.0.5
s
C.1
s
D.2s
【例13】单摆在振动过程中,摆动幅度越来越小这是因为:(
D
)
A.能量正在逐渐消灭
B.动能正在转化为势能
C.机械能守恒
D.总能量守恒,减少的动能转化为内能
【例14】任何物体都有一定的固有频率.如果把人作为一个振动系统,在水平方向的固有频率约为3
Hz~6
Hz,在竖直方向的固有频率约为4
Hz~8
Hz.拖拉机、风镐、风铲、铆钉机等的操作工在工作时将做________振动,这时若操作工的固有频率与振源振动的频率________,就会对操作工的健康造成伤害.为保证操作工的安全与健康,有关部门作出规定:用于操作的各类振动机械的频率必须大于20
Hz,这是为了防止________所造成的伤害.
答案:受迫
接近或相等
共振
【例15】如图所示,一轻弹簧的左端固定在竖直墙上,右端与质量为M的滑块相连,组成弹簧振子,在光滑的水平面上做简谐运动.当滑块运动到右侧最大位移处时,在滑块上轻轻放上一木块组成新振子,继续做简谐运动.新振子的运动过程与原振子的运动过程相比(
AC
)
A.新振子的最大速度比原振子的最大速度小
B.新振子的最大动能比原振子的最大动能小
C.新振子的振动周期比原振子的振动周期大
D.新振子的振幅比原振子的振幅小
【例16】右图为一单摆的共振曲线,则该单摆的摆长约为多少?共振时单摆的振幅多大?(g取10m/s2)
解:由图可知,单摆在f驱=0.5Hz时振动最剧烈,表明此时发生了共振,振幅为10cm。
由,得:L===1.01m
【例17】如图1所示,三角架质量为M,沿其中轴线用两根轻弹簧拴一质量为m的小球,原来三角架静止在水平面上.现使小球做上下振动,已知三角架对水平面的压力最小为零,求:
(1)此时小球的瞬时加速度;
(2)若上、下两弹簧的劲度系数均为k,则小球做简谐运动的振幅为多少
答案:
(1)
g,方向竖直向下
(2)
解析:(1)当小球上下振动过程中,三角架对水平面的压力最小为零,则上下两根弹簧对三角架的作用力大小为Mg,方向向下,小球此时受弹簧的弹力大小为Mg,方向向上,故小球所受合力为(m+M)g,方向向下,小球此时运动到上面最高点即位移大小等于振幅处.根据牛顿第二定律,小球的瞬时加速度的最大值为:am=,加速度的方向为竖直向下.
(2)小球由平衡位置上升至最高点时,上面的弹簧(相当于压缩x)对小球会产生向下的弹力kx,下面的弹簧(相当于伸长x)会对小球产生向下的弹力kx,两根弹簧对小球的作用力为2kx,故最大回复力大小F回=2kA,而最高时F回=(M+m)g,故A=.
【例18】如图,A、B两单摆摆长分别为
、,两球静止时刚好接触,且重心等高、质量相等。今把A球从平衡位置向右拉开一个微小角度,然后无初速释放,于是AB将发生一系列弹性正碰,设碰撞后两球速度互换,碰撞时间不计.则释放A球后20s内两球碰撞多少次?
解:先求出AB摆长的单摆周期:
A释放后经与B发生碰撞,碰后速度交换,A静止,B球向左摆动,再经又摆回与A发生碰撞,碰后B静止,A向右运动,再经回到最右边。可见每经过,A、B发生两次碰撞,A又回到释放初的最右位置。所以有:
表明经过了13个碰撞周期,碰了26次,而0。5s正好是TA/4,所以第20s末A刚好回到平衡位置,第27次碰撞正在发生.
R
O
a
θ
θ
θ
同课章节目录
- 第1章 机械振动
- 导 入 从我国古代的“鱼洗”说起
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 生活中的振动
- 第2章 机械波
- 导 入 身边的波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第3章 电磁波
- 导 入 无处不在的电磁波
- 第1节 电磁波的产生
- 第2节 电磁波的发射、传播和接收
- 第3节 电磁波的应用及防护
- 专题探究 振动与波的实验与调研
- 第4章 光的折射与全反射
- 导 入 美妙的彩虹
- 第1节 光的折射定律
- 第2节 光的全反射
- 第3节 光导纤维及其应用
- 第5章 光的干涉 衍射 偏振
- 导 入 从五彩斑斓的肥皂泡说起
- 第1节 光的干涉
- 第2节 光的衍射
- 第3节 光的偏振
- 第4节 激光与全息照相
- 专题探究 光学部分的实验与调研
- 第6章 相对论与天体物理
- 导 入 从双生子佯谬谈起
- 第1节 牛顿眼中的世界
- 第2节 爱因斯坦眼中的世界
- 第3节 广义相对论初步
- 第4节 探索宇宙
