湖南省蓝山县第二中学2015-2016学年高一上学期入学编班考试数学试题
文档属性
| 名称 | 湖南省蓝山县第二中学2015-2016学年高一上学期入学编班考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-31 12:12:42 | ||
图片预览



文档简介
蓝山二中2016年高一入学测试数学试题
一、选择题(本大题共12小题,每小题4分,共48分)
1.64的平方根是( )
A.8
B.4
C.±8
D.±4
2.下面四个手机应用图标中是轴对称图形的是( )
A.
( http: / / www.21cnjy.com ) B.
( http: / / www.21cnjy.com ) C.
( http: / / www.21cnjy.com ) D.
( http: / / www.21cnjy.com )
3.
实数a,b在数轴上的对应点的位置如图所示,则正确的结论是
A.
a
B.
C.
D.
4.下面四个立体图形中,主视图是圆的是(
)
A.
B.
C.
D.
5.下列运算正确的是(
)
A.a+2a=2a2
B.(﹣2ab2)2
=4a2b4
C.a6÷a3=a2
D.(a﹣3)2
=a2﹣9
6.
我校学生篮球队10名同学的身高分别为(单位:cm):167,168,165,168,166,170,170,176,170,175.
则下列说法错误的是( )
A.
这组数据的众数是170
B.
这组数据的中位数是169
C.
这组数据的平均数是169.5
D.
若从10名学生中任选1名学生当队长,则这名学生的身高不低于168的概率为
7.
如图,在平行四边形中,为的中点,的周长为1,则的周长为(
)
A.1
B.2
C.3
D.4
8.
若则代数式的取值共有(
)
A.1个
B.2个
C.3个
D.4个
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
A.1
B.2
C.3
D.4
10.若不等式组恰有两个整数解,则的取值范围是( )
A.
B.
C.
D.
11.某商品原价188元,连续两次降价后售价为118元,下列所列方程中正确的是( )
A.
B.
C.
D.
12.小明同学从家里去学校,开始采用匀速步行,走了一段路后,发觉照这样走下去会迟到,于是匀速跑步完成余下的路程,下面坐标系中,横轴表示小明从家里出发后的时间t,纵轴表示小明距离学校的路程S,则S与t之间函数关系的图像大致是(
)
二、填空题(本大题共8小题,每小题4分,共32分)
13.
据统计,2015年广州地铁日均客运量均为6
591
000人次,将6
591
000用科学记数法
表示为
.
14.
分解因式:
15.
两个正数
满足,则式子的值为
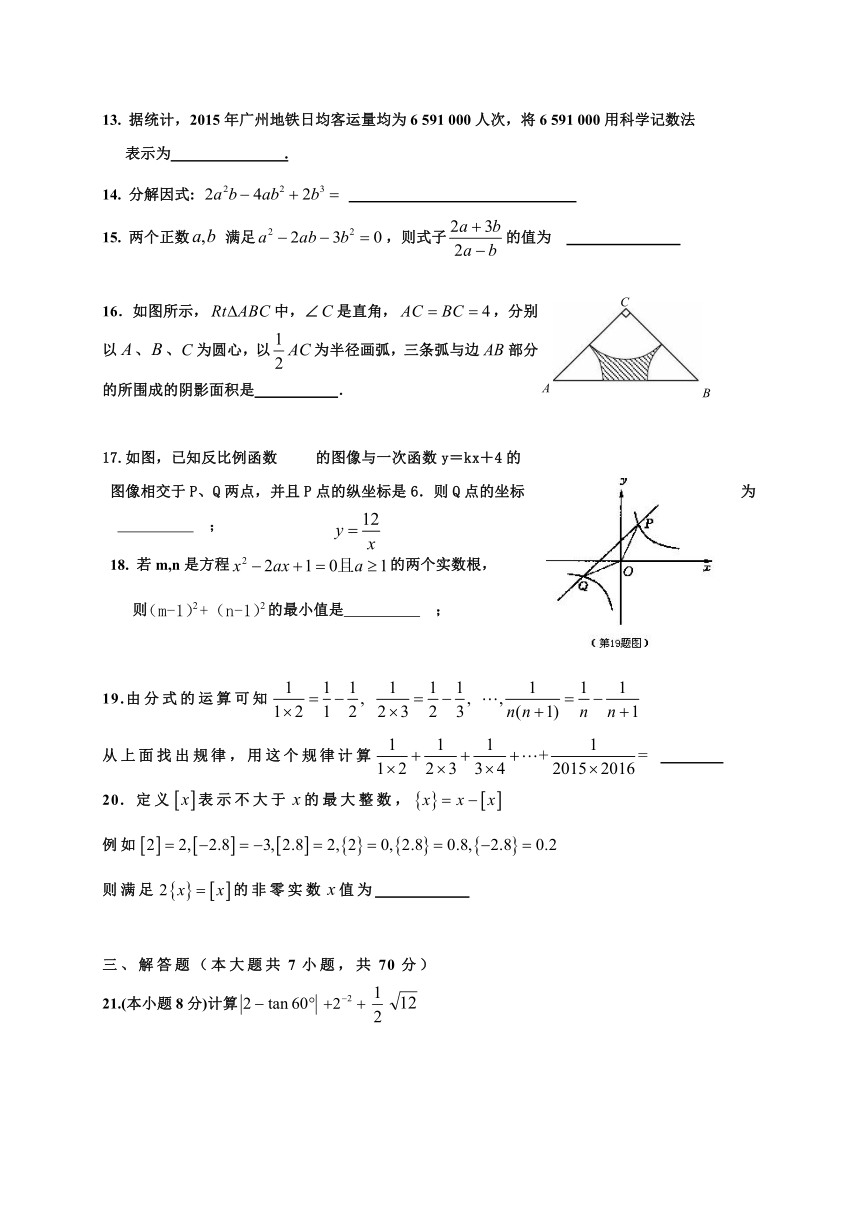
16.如图所示,中,∠是直角,,分别
以、、为圆心,以为半径画弧,三条弧与边部分
的所围成的阴影面积是
.
17.如图,已知反比例函数
的图像与一次函数y=kx+4的
图像相交于P、Q两点,并且P点的纵坐标是6.则Q点的坐标为
;
18.
若m,n是方程的两个实数根,
则的最小值是
;
19.由分式的运算可知
从上面找出规律,用这个规律计算
20.
定义表示不大于的最大整数,
例如
则满足的非零实数值为
三、解答题(本大题共7小题,共70分)
21.(本小题8分)计算
22.(本小题8分)
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
组别
A
B
C
D
E
时间t(分钟)
t<40
40≤t<60
60≤t<80
80≤t<100
t≥100
人数
12
30
a
24
12
(1)求出本次被调查的学生数;
(2)请求出统计表中a的值;
(3)求每天体育锻炼时间不小于100分钟学生人数的百分比所占扇形的圆心角度数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间
不少于1小时的学生人数.
23.(本小题10分)
如图,平行四边形ABCD中,BD⊥AD,∠A=45°,
E、F
分别
是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1
时,求AE的长.
24.(本小题10分)如图,某山脚下西端A处与东端B处直线距离800(1+)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知这座山的西端A的坡角是45°,东端B的坡角是30°,小军的上山行走速度为米/秒.若小明与小军同时到达山顶C处,则小明的上山行走速度是多少?
25.(本小题10分)如图,AB是⊙O的
( http: / / www.21cnjy.com )直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
26.
(本小题12分)已知关于x的方程x2-(2k+1)x+4(k-
)=0.
⑴
求证:无论k取何值,这个方程总有实数根;
⑵
若等腰三角形ABC的一边长a=4,另两边的长b、c恰好是这个方程的两个根,求三角形ABC的周长.
27.(本小题12分)
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象顶点为M(2,9)且过点C(8,0).
(1)求该二次函数的表达式;
(2)点D的坐标为(0,4),点F为该二次
( http: / / www.21cnjy.com )函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①若F的横坐标为3,求S的值;
②是否存在点F,使点E也落在该二次函数图象上.若存在,求出F的坐标;若不存在,说明理由。
高一数学测试参考答案
选择题
CDDBC,DBBCA,
BD
解答题
21.
每小题2分(1)12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42;
(3)圆心角度数36度;
(4)每天体育锻炼时间不少于1小时的学生人数是:2400×=1560(人)
23.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
………………………1分
∴∠OBE
=∠ODF.
………………………2分
在△OBE与△ODF中,
∵
∴△OBE≌△ODF(AAS).………………………4分
∴BO=DO.
………………………5分
(2)解:∵EF⊥AB,AB
∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
…………………6分
∴AE=GE
…………7分
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
……………8分
∴DG=DO
∴OF=FG=
1
……………9分
由(1)可知,OE=
OF=1
∴GE=OE+OF+FG=3
∴AE=3
……………10分
(本题有多种解法,请参照此评分标准给分.)
24.(10分)解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,∴AD=CD=x米,∴AC=x.
在Rt△BCD中,∵∠B=30°,
∴BC===2x,
∵小军的行走速度为米/秒.若小明与小军同时到达山顶C处,
∴=,解得a=1米/秒.答:小明的行走速度是1米/秒.
25.(本题10分)(1)证明:连接CO,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠OCA=∠CAE,
∴OC∥FD,
∵CE⊥DF,
∴OC⊥CE,
∴CE是⊙O的切线;................................5分
(2)证明:连接BC,
在Rt△ACE中,AC===,
∵AB是⊙O的直径,∴∠BCA=90°,∴∠BCA=∠CEA,
∵∠CAE=∠CAB,∴△ABC∽△ACE,∴=,
∴,∴AB=5,
∴AO=2.5,即⊙O的半径为2.5.
26.(12分)解:(1)
所以:无论k取何值,这个方程总有实数根。-------5分
(2)三角形ABC为等腰三角形,可能有两种情况:
1)b或c中至少有一个等于a=
4,即:方程x2-(2k+1)x+4(k-
)=0有一根为4,
可得k=,方程为x2-6x+8=0.另一根为2,此时三角形ABC周长为10;------9分
2)b=c时,
得k=,方程为x2-
4x+4=0.得b=c=2,
此时ABC不能构成三角形;
综上,三角形ABC周长为10。
--------------------12分
27.(12分)【解答】解:(1)抛物线的解析式为y=﹣x2+x+8;.................4分
(2)①
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF﹣S△OCD=25,
∵四边形CDEF为平行四边形,
∴S为50;..............................................................................8分
②∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF,
( http: / / www.21cnjy.com )利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,
∵点C向左平移8个单位,再向上平移4个单位得到点D,
∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣
t2+t+12),
∵E(t﹣8,﹣
t2+t+12)在抛物线上,
∴﹣(t﹣8)2+t﹣8+8=﹣t2+t+12,解得t=7,
当t=7时,S△CDF=﹣(7﹣3)2+25=9,
∴此时S=2S△CDF=18..............................4分
A
B
C
一、选择题(本大题共12小题,每小题4分,共48分)
1.64的平方根是( )
A.8
B.4
C.±8
D.±4
2.下面四个手机应用图标中是轴对称图形的是( )
A.
( http: / / www.21cnjy.com ) B.
( http: / / www.21cnjy.com ) C.
( http: / / www.21cnjy.com ) D.
( http: / / www.21cnjy.com )
3.
实数a,b在数轴上的对应点的位置如图所示,则正确的结论是
A.
a
B.
C.
D.
4.下面四个立体图形中,主视图是圆的是(
)
A.
B.
C.
D.
5.下列运算正确的是(
)
A.a+2a=2a2
B.(﹣2ab2)2
=4a2b4
C.a6÷a3=a2
D.(a﹣3)2
=a2﹣9
6.
我校学生篮球队10名同学的身高分别为(单位:cm):167,168,165,168,166,170,170,176,170,175.
则下列说法错误的是( )
A.
这组数据的众数是170
B.
这组数据的中位数是169
C.
这组数据的平均数是169.5
D.
若从10名学生中任选1名学生当队长,则这名学生的身高不低于168的概率为
7.
如图,在平行四边形中,为的中点,的周长为1,则的周长为(
)
A.1
B.2
C.3
D.4
8.
若则代数式的取值共有(
)
A.1个
B.2个
C.3个
D.4个
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
A.1
B.2
C.3
D.4
10.若不等式组恰有两个整数解,则的取值范围是( )
A.
B.
C.
D.
11.某商品原价188元,连续两次降价后售价为118元,下列所列方程中正确的是( )
A.
B.
C.
D.
12.小明同学从家里去学校,开始采用匀速步行,走了一段路后,发觉照这样走下去会迟到,于是匀速跑步完成余下的路程,下面坐标系中,横轴表示小明从家里出发后的时间t,纵轴表示小明距离学校的路程S,则S与t之间函数关系的图像大致是(
)
二、填空题(本大题共8小题,每小题4分,共32分)
13.
据统计,2015年广州地铁日均客运量均为6
591
000人次,将6
591
000用科学记数法
表示为
.
14.
分解因式:
15.
两个正数
满足,则式子的值为
16.如图所示,中,∠是直角,,分别
以、、为圆心,以为半径画弧,三条弧与边部分
的所围成的阴影面积是
.
17.如图,已知反比例函数
的图像与一次函数y=kx+4的
图像相交于P、Q两点,并且P点的纵坐标是6.则Q点的坐标为
;
18.
若m,n是方程的两个实数根,
则的最小值是
;
19.由分式的运算可知
从上面找出规律,用这个规律计算
20.
定义表示不大于的最大整数,
例如
则满足的非零实数值为
三、解答题(本大题共7小题,共70分)
21.(本小题8分)计算
22.(本小题8分)
近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计扇形图.
组别
A
B
C
D
E
时间t(分钟)
t<40
40≤t<60
60≤t<80
80≤t<100
t≥100
人数
12
30
a
24
12
(1)求出本次被调查的学生数;
(2)请求出统计表中a的值;
(3)求每天体育锻炼时间不小于100分钟学生人数的百分比所占扇形的圆心角度数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间
不少于1小时的学生人数.
23.(本小题10分)
如图,平行四边形ABCD中,BD⊥AD,∠A=45°,
E、F
分别
是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1
时,求AE的长.
24.(本小题10分)如图,某山脚下西端A处与东端B处直线距离800(1+)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知这座山的西端A的坡角是45°,东端B的坡角是30°,小军的上山行走速度为米/秒.若小明与小军同时到达山顶C处,则小明的上山行走速度是多少?
25.(本小题10分)如图,AB是⊙O的
( http: / / www.21cnjy.com )直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
26.
(本小题12分)已知关于x的方程x2-(2k+1)x+4(k-
)=0.
⑴
求证:无论k取何值,这个方程总有实数根;
⑵
若等腰三角形ABC的一边长a=4,另两边的长b、c恰好是这个方程的两个根,求三角形ABC的周长.
27.(本小题12分)
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象顶点为M(2,9)且过点C(8,0).
(1)求该二次函数的表达式;
(2)点D的坐标为(0,4),点F为该二次
( http: / / www.21cnjy.com )函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①若F的横坐标为3,求S的值;
②是否存在点F,使点E也落在该二次函数图象上.若存在,求出F的坐标;若不存在,说明理由。
高一数学测试参考答案
选择题
CDDBC,DBBCA,
BD
解答题
21.
每小题2分(1)12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42;
(3)圆心角度数36度;
(4)每天体育锻炼时间不少于1小时的学生人数是:2400×=1560(人)
23.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
………………………1分
∴∠OBE
=∠ODF.
………………………2分
在△OBE与△ODF中,
∵
∴△OBE≌△ODF(AAS).………………………4分
∴BO=DO.
………………………5分
(2)解:∵EF⊥AB,AB
∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
…………………6分
∴AE=GE
…………7分
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
……………8分
∴DG=DO
∴OF=FG=
1
……………9分
由(1)可知,OE=
OF=1
∴GE=OE+OF+FG=3
∴AE=3
……………10分
(本题有多种解法,请参照此评分标准给分.)
24.(10分)解:过点C作CD⊥AB于点D,设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,∴AD=CD=x米,∴AC=x.
在Rt△BCD中,∵∠B=30°,
∴BC===2x,
∵小军的行走速度为米/秒.若小明与小军同时到达山顶C处,
∴=,解得a=1米/秒.答:小明的行走速度是1米/秒.
25.(本题10分)(1)证明:连接CO,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠OCA=∠CAE,
∴OC∥FD,
∵CE⊥DF,
∴OC⊥CE,
∴CE是⊙O的切线;................................5分
(2)证明:连接BC,
在Rt△ACE中,AC===,
∵AB是⊙O的直径,∴∠BCA=90°,∴∠BCA=∠CEA,
∵∠CAE=∠CAB,∴△ABC∽△ACE,∴=,
∴,∴AB=5,
∴AO=2.5,即⊙O的半径为2.5.
26.(12分)解:(1)
所以:无论k取何值,这个方程总有实数根。-------5分
(2)三角形ABC为等腰三角形,可能有两种情况:
1)b或c中至少有一个等于a=
4,即:方程x2-(2k+1)x+4(k-
)=0有一根为4,
可得k=,方程为x2-6x+8=0.另一根为2,此时三角形ABC周长为10;------9分
2)b=c时,
得k=,方程为x2-
4x+4=0.得b=c=2,
此时ABC不能构成三角形;
综上,三角形ABC周长为10。
--------------------12分
27.(12分)【解答】解:(1)抛物线的解析式为y=﹣x2+x+8;.................4分
(2)①
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF﹣S△OCD=25,
∵四边形CDEF为平行四边形,
∴S为50;..............................................................................8分
②∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF,
( http: / / www.21cnjy.com )利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,
∵点C向左平移8个单位,再向上平移4个单位得到点D,
∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,﹣
t2+t+12),
∵E(t﹣8,﹣
t2+t+12)在抛物线上,
∴﹣(t﹣8)2+t﹣8+8=﹣t2+t+12,解得t=7,
当t=7时,S△CDF=﹣(7﹣3)2+25=9,
∴此时S=2S△CDF=18..............................4分
A
B
C
同课章节目录
