函数的极值与导数

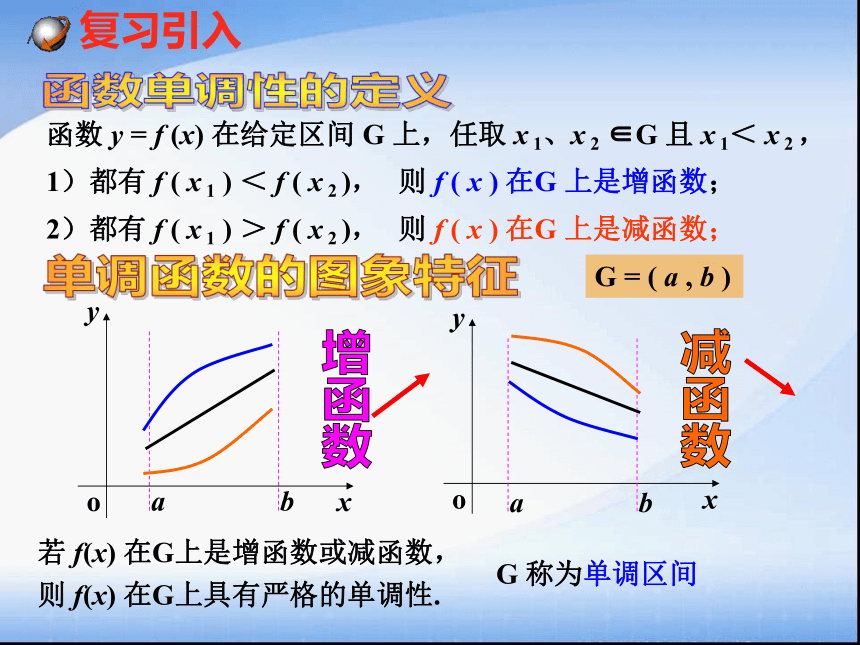
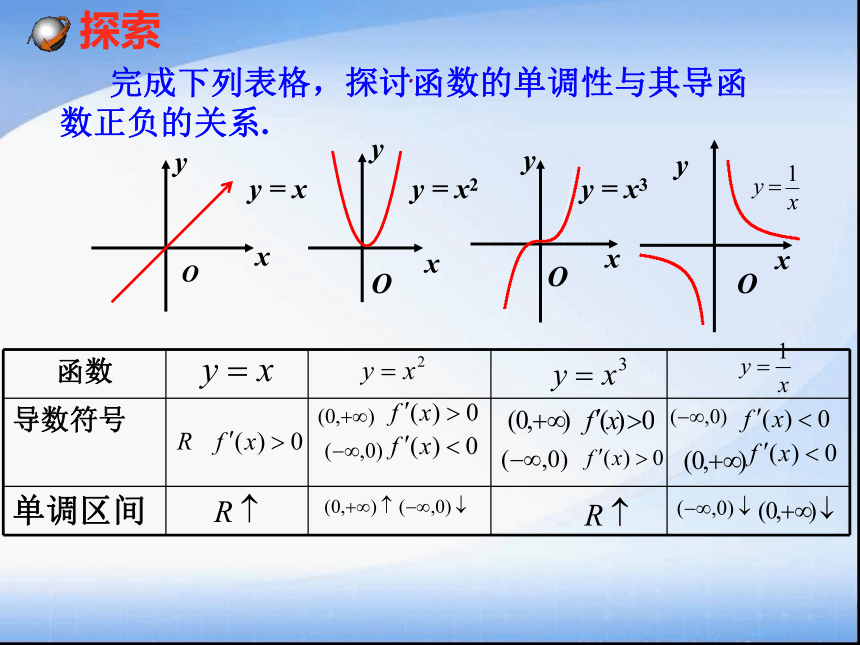
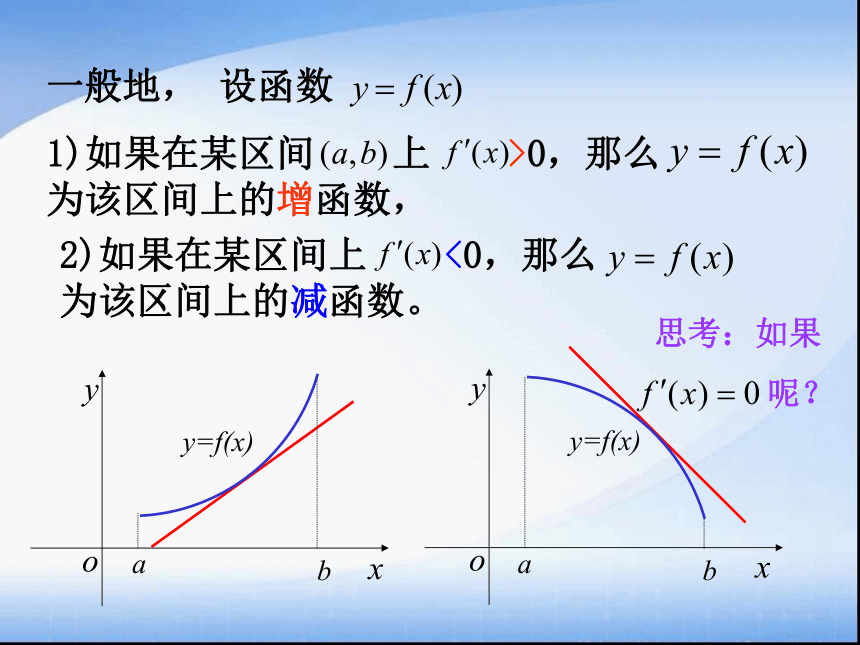
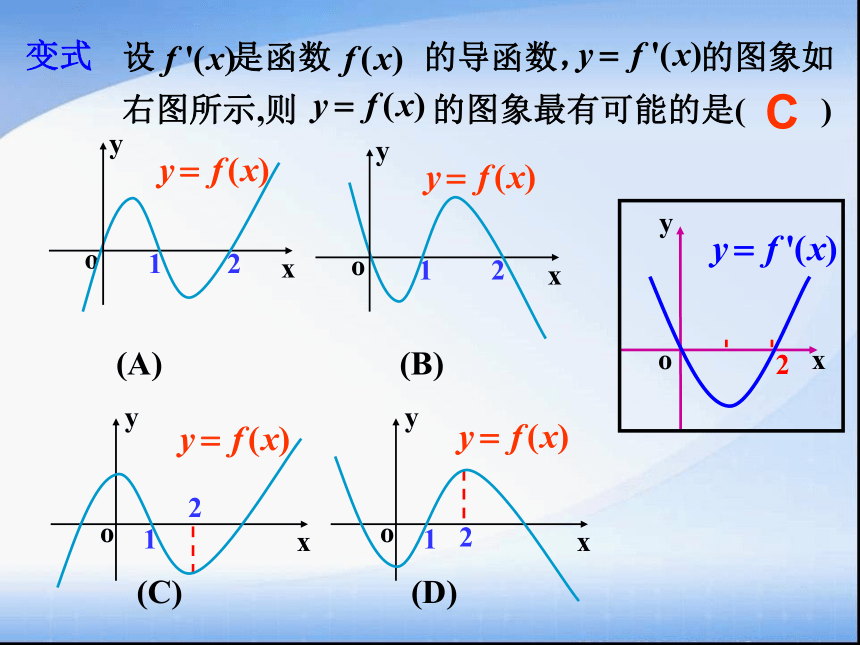
课件16张PPT。1.3导数在研究函数中的应用1.3.1函数的单调性与导数函数 y = f (x) 在给定区间 G 上，任取 x 1、x 2 ∈G 且 x 1＜ x 2 ，函数单调性的定义单调函数的图象特征1）都有 f ( x 1 ) ＜ f ( x 2 )，则 f ( x ) 在G 上是增函数；2）都有 f ( x 1 ) ＞ f ( x 2 )，则 f ( x ) 在G 上是减函数；若 f(x) 在G上是增函数或减函数，增函数减函数则 f(x) 在G上具有严格的单调性.G 称为单调区间G = ( a , b )思考 完成下列表格，探讨函数的单调性与其导函数正负的关系.yyxyOy = xxxOOy = x3xyOy = x22)如果在某区间上 <0，那么 为该区间上的减函数。例1已知导函数f/(x)的下列信息：当10；当x>4，或x<1时， f/(x)<0当x=4,或x=1时， f/(x)=0试画出函数f(x)图像的大致形状四、数学运用:C变式例2判断下列函数的单调性，并求出单调区间：四、数学运用:四、数学运用:利用导数讨论函数单调性的一般步骤:(4)写出单调区间练习：判断下列函数的单调性，并求出单调区间：四、数学运用:四、数学运用:变式1变式2已知变式
在某个区间 如果函数 是单课后思考：（或 ）吗？调递增的（或单调递减的），那么五、小结: 3. 利用导数讨论函数的单调性1、函数的单调性与导数的关系.(首先要确定函数的定义域,解决问题的过程中,只能在函数的定义域内)2、能根据导函数的特别绘制大致函数图象.谢谢！再见