六年级上测数学五完美的图形——圆单元测试题(含答案)
文档属性
| 名称 | 六年级上测数学五完美的图形——圆单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 92.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-31 13:48:58 | ||
图片预览




文档简介
青岛版六三制新六年级(上)小升初题单元试卷:五 完美的图形---圆(04)
一、选择题(共9小题)
1.一张长方形纸长12厘米,宽8厘米,在这张长方形的纸中剪一个最大的圆,这个圆的面积是( )平方厘米.
A.113.04 B.50.24 C.96 D.45.76
2.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形的( )
A. B. C. D.
3.圆的半径扩大2倍,圆的面积就扩大( )倍.
A.2 B.4 C.8 D.16
4.小圆的直径等于大圆的半径,小圆的面积是大圆面积的( )
A. B. C. D.
5.大圆与小圆半径的比是5:4,大圆面积与小圆面积的比是( )
A.5:4 B.10:8 C.25:16
6.一个圆环,它的外圆直径是内圆直径的2倍,这个圆环的面积( )
A.比内圆面积大 B.比内圆面积小
C.与内圆面积相等
7.小圆和大圆的半径分别是2厘米和5厘米,小圆与大圆的面积之比是( )
A.2:5 B.4:10 C.4:25 D.2:10
8.圆的半径扩大3倍,面积扩大( )
A.3倍 B.6倍 C.9倍
9.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形面积的( )
A. B. C. D.
二、填空题(共17小题)
10.大圆的直径是小圆半径的2倍,小圆的面积是大圆面积的倍. (判断对错)
11.已知圆的直径为20厘米,则圆的面积为 平方厘米.(π取3.14)
12.半圆的面积是它所在圆面积的一半. .
13.周长相等的两个圆,它们的面积也一定相等. .(判断对错)
14.在一个圆内,以它的半径为边长做一个正方形,已知正方形面积是36cm2,圆的面积是 cm2.
15.半圆的面积是这个圆的面积的一半. (判断对错)
16.从一个边长为20厘米的正方形纸片中,剪出一个最大的圆,这个圆的面积是 平方厘米.
17.周长相等的两个圆,面积不一定相等. .(判断对错)
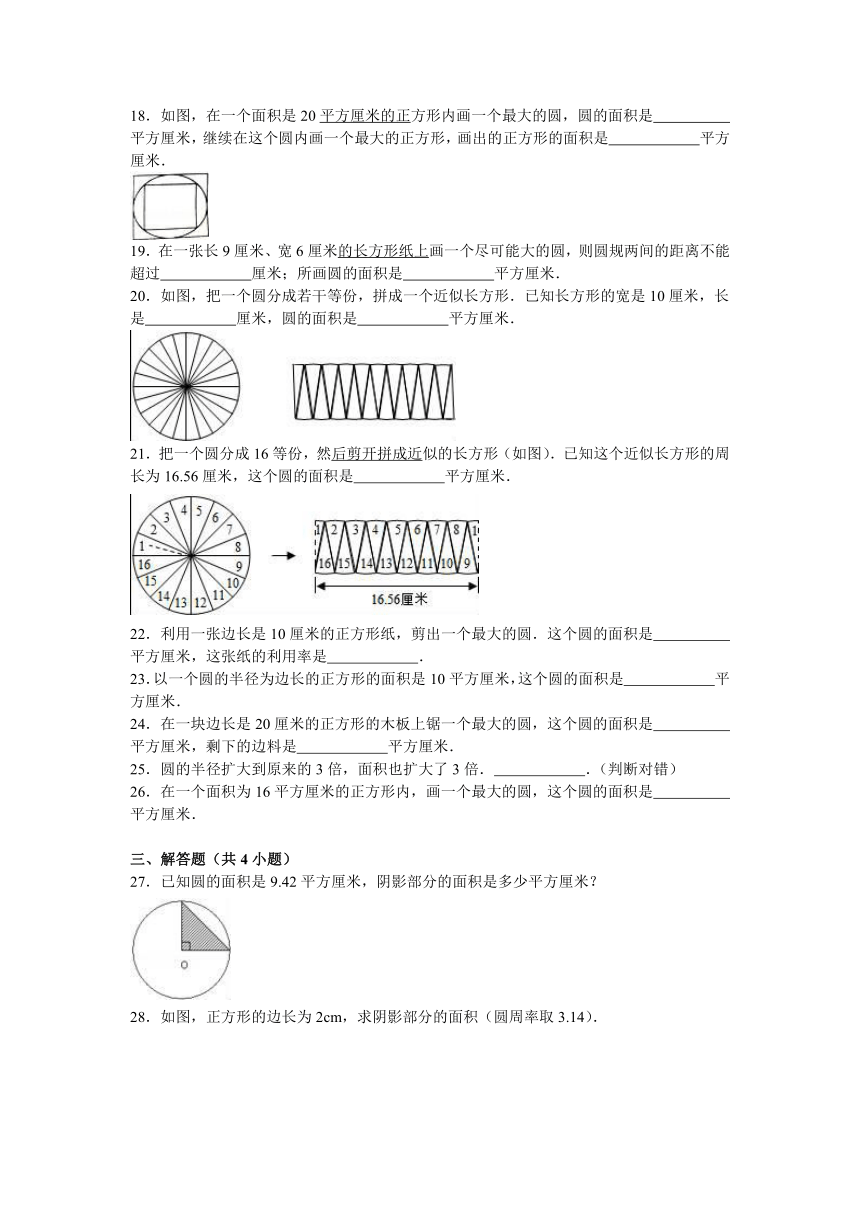
18.如图,在一个面积是20平方厘米的正方形内画一个最大的圆,圆的面积是 平方厘米,继续在这个圆内画一个最大的正方形,画出的正方形的面积是 平方厘米.
19.在一张长9厘米、宽6厘米的长方形纸上画一个尽可能大的圆,则圆规两间的距离不能超过 厘米;所画圆的面积是 平方厘米.
20.如图,把一个圆分成若干等份,拼成一个近似长方形.已知长方形的宽是10厘米,长是 厘米,圆的面积是 平方厘米.
21.把一个圆分成16等份,然后剪开拼成近似的长方形(如图).已知这个近似长方形的周长为16.56厘米,这个圆的面积是 平方厘米.
22.利用一张边长是10厘米的正方形纸,剪出一个最大的圆.这个圆的面积是 平方厘米,这张纸的利用率是 .
23.以一个圆的半径为边长的正方形的面积是10平方厘米,这个圆的面积是 平方厘米.
24.在一块边长是20厘米的正方形的木板上锯一个最大的圆,这个圆的面积是 平方厘米,剩下的边料是 平方厘米.
25.圆的半径扩大到原来的3倍,面积也扩大了3倍. .(判断对错)
26.在一个面积为16平方厘米的正方形内,画一个最大的圆,这个圆的面积是 平方厘米.
三、解答题(共4小题)
27.已知圆的面积是9.42平方厘米,阴影部分的面积是多少平方厘米?
28.如图,正方形的边长为2cm,求阴影部分的面积(圆周率取3.14).
29.已知长方形面积与圆面积相等.已知圆的半径是3厘米,求阴影部分的面积.
30.小方桌的边长是1米,把它的四边撑开就成了一张圆桌(如图)求圆桌的面积.
青岛版六三制新六年级(上)小升初题单元试卷:五 完美的图形---圆(04)
参考答案与试题解析
一、选择题(共9小题)
1.一张长方形纸长12厘米,宽8厘米,在这张长方形的纸中剪一个最大的圆,这个圆的面积是( )平方厘米.
A.113.04 B.50.24 C.96 D.45.76
【考点】圆、圆环的面积.
【分析】在这个长方形纸上画的最大圆的直径应等于长方形的宽,长方形的宽已知,从而利用圆的面积公式:s=πr2,即可求出圆的面积.
【解答】解:这个圆的直径是8厘米;
圆的面积:3.14×(8÷2)2,
=3.14×16,
=50.24(平方厘米).
答:这个圆的面积是50.24平方厘米.
故选B.
2.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形的( )
A. B. C. D.
【考点】圆、圆环的面积;长方形、正方形的面积.
【分析】根据题意可知:这个圆的直径就是正方形的边长,再依据圆的面积公式:s=πr2即可求其面积,再利用圆的面积除以正方形的面积即可解答问题.
【解答】解:π×(6÷2)2
=π×9
=9π(平方厘米),
正方形的面积是:6×6=36(平方厘米)
所以9π÷36=,
答:圆的面积占正方形的.
故选:C.
3.圆的半径扩大2倍,圆的面积就扩大( )倍.
A.2 B.4 C.8 D.16
【考点】圆、圆环的面积.
【分析】这道题中圆的半径不是一个具体的数字,像这种情况下,我们可以采用假设法,把它的半径假设成一个具体的数,根据面积公式算出它们原来和扩大后的面积,再用除法算一算它的面积扩大多少倍.
【解答】解:假设这个圆原来的半径是1厘米,则扩大2倍后半径是2厘米
原来圆的面积S=πr2=3.14×12=3.14(平方厘米)
扩大后圆的面积S=πr2=3.14×22=12.56(平方厘米)
12.56÷3.14=4倍
故选:B.
4.小圆的直径等于大圆的半径,小圆的面积是大圆面积的( )
A. B. C. D.
【考点】圆、圆环的面积.
【分析】设小圆的直径等于大圆的半径是1,利用圆的面积公式计算出它们的面积即可解答.
【解答】解:设小圆的直径等于大圆的半径是1,则:
小圆的面积为:π=;
大圆的面积为:π×12=π;
所以小圆的面积是大圆的面积的.
故选:B.
5.大圆与小圆半径的比是5:4,大圆面积与小圆面积的比是( )
A.5:4 B.10:8 C.25:16
【考点】圆、圆环的面积.
【分析】根据大圆与小圆半径的比是5:4,可把大圆的半径看作5份数,小圆的半径看作4份数;进而根据圆的面积=πr2,分别求出大圆的面积和小圆的面积,然后根据题意,写出比值即可.
【解答】解:(π×52):(π×42)
=25π:16π
=25:16
答:大圆面积与小圆面积比是25:16.
故选:C.
6.一个圆环,它的外圆直径是内圆直径的2倍,这个圆环的面积( )
A.比内圆面积大 B.比内圆面积小
C.与内圆面积相等
【考点】圆、圆环的面积.
【分析】根据“外圆直径是内圆直径的2倍”,知道外圆半径是内圆半径的2倍,由此根据圆的面积公式S=πr2,分别用内圆的半径表示出两个圆的面积,进而得出圆环的面积,再与内圆的面积比较,从而做出选择.
【解答】解:设内圆的半径为r,则外圆的半径为2r,
所以圆环的面积是π(2r)2﹣πr2=3πr2>πr2,
所以这个圆环的面积比内圆面积大;
故选:A.
7.小圆和大圆的半径分别是2厘米和5厘米,小圆与大圆的面积之比是( )
A.2:5 B.4:10 C.4:25 D.2:10
【考点】圆、圆环的面积;比的意义.
【分析】根据圆的面积公式:S=πr2,据此求出大小圆的面积,然后求比,再根据比的基本性质化简比.
【解答】解:小圆的面积是:π×22=4π,
大圆的面积是:π×52=25π,
小圆面积和大圆面积的比是:4π:25π=4:25;
故选:C.
8.圆的半径扩大3倍,面积扩大( )
A.3倍 B.6倍 C.9倍
【考点】圆、圆环的面积.
【分析】这道题中圆的半径不是一个具体的数字,像这种情况下,我们可以采用假设法,把它的半径假设成一个具体的数,根据面积公式算出它们原来和扩大后的面积,再用除法算一算它的面积扩大多少倍即可判断.
【解答】解:假设这个圆原来的半径是1厘米,则扩大3倍后半径是3厘米,
原来圆的面积S=πr2=π×12=π(平方厘米),
扩大后圆的面积S=πr2=π×32=9π(平方厘米),
9π÷π=9倍;
答:圆的半径扩大3倍,面积扩大9倍.
故选:C.
9.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形面积的( )
A. B. C. D.
【考点】圆、圆环的面积;分数除法应用题;长方形、正方形的面积.
【分析】根据题意可知:这个圆的直径就是正方形的边长,再依据圆的面积公式:s=πr2即可求其面积,再利用圆的面积除以正方形的面积即可解答问题.
【解答】解:π×(6÷2)2
=π×9
=9π(平方厘米),
正方形的面积是:6×6=36(平方厘米)
所以9π÷36=,
答:圆的面积占正方形的.
故选:A.
二、填空题(共17小题)
10.大圆的直径是小圆半径的2倍,小圆的面积是大圆面积的倍. × (判断对错)
【考点】圆、圆环的面积.
【分析】因为大圆的直径是小圆半径的2倍,设小圆的半径是r,大圆的直径是2r,大圆的半径是r,由此根据圆的面积公式得出小圆的面积与大圆的面积相等.
【解答】解:设小圆的半径是r,大圆的直径是2r,大圆的半径是r
所以小圆的面积与大圆的面积相等;
故答案为:×.
11.已知圆的直径为20厘米,则圆的面积为 314 平方厘米.(π取3.14)
【考点】圆、圆环的面积.
【分析】圆的面积=πr2,由此代入数据即可解答.
【解答】解:3.14×(20÷2)2
=3.14×100
=314(平方厘米)
答:圆的面积是314平方厘米.
故答案为:314.
12.半圆的面积是它所在圆面积的一半. √ .
【考点】圆、圆环的面积.
【分析】要判断对或错,通过计算即可得出答案.
【解答】解:圆的面积=πr2,
半圆的面积=πr2,
故答案为:√.
13.周长相等的两个圆,它们的面积也一定相等. √ .(判断对错)
【考点】圆、圆环的面积;圆、圆环的周长.
【分析】根据圆的周长公式、面积公式与半径的关系,可以得出结论.
【解答】解:根据圆的周长公式:C=2πr,可以得出两个圆周长相等,则它们的半径就相等;
再根据圆的面积公式:S=πr2,半径相等则面积就相等.
故答案为:√.
14.在一个圆内,以它的半径为边长做一个正方形,已知正方形面积是36cm2,圆的面积是 113.04 cm2.
【考点】圆、圆环的面积.
【分析】根据题干,设圆的半径是r,则r2=36,据此代入圆的面积=πr2中即可求出圆的面积.
【解答】解:根据题干分析可得:设圆的半径是r,则r2=36,
所以圆的面积是:3.14×36=113.04(平方厘米)
答:圆的面积是113.04平方厘米.
故答案为:113.04.
15.半圆的面积是这个圆的面积的一半. √ (判断对错)
【考点】圆、圆环的面积.
【分析】根据圆的面积公式:s=πr2,半圆的面积就是这个圆面积的一半.
【解答】解:圆的面积=πr2,
半圆的面积=πr2,
因此,半圆的面积是圆的面积的一半.此说法正确.
故答案为:√.
16.从一个边长为20厘米的正方形纸片中,剪出一个最大的圆,这个圆的面积是 314 平方厘米.
【考点】圆、圆环的面积.
【分析】由题意知,在正方形内剪出的面积最大的圆形纸片,其直径就等于正方形的边长,即20厘米;要求这个圆形的面积,可利用圆面积公式S=πr2求得即可.
【解答】解:3.14×(20÷2)2
=3.14×100
=314(平方厘米).
答:这个圆的面积是314平方厘米.
故答案为:314.
17.周长相等的两个圆,面积不一定相等. × .(判断对错)
【考点】圆、圆环的面积;圆、圆环的周长.
【分析】因为两个圆周长相等,周长公式:c=2πr,因为圆周率是一定的,所以两个圆的半径相等,根据圆的面积公式S=πr2,两个圆的面积一定相等.
【解答】解:因为圆周率是一定的,两个圆的周长相等,即半径相等,所以它们的面积一定相等.
故答案为:×.
18.如图,在一个面积是20平方厘米的正方形内画一个最大的圆,圆的面积是 15.7 平方厘米,继续在这个圆内画一个最大的正方形,画出的正方形的面积是 10 平方厘米.
【考点】圆、圆环的面积;长方形、正方形的面积.
【分析】由题意可知:这个最大圆的直径应该等于大正方形的边长,据此利用圆的面积公式即可求出圆的面积;小正方形的对角线等于圆的直径,则小正方形的面积对角线的平方的2倍,据此解答即可.
【解答】解:(1)设正方形的边长为a,圆的半径为,
则a2=20平方厘米,
圆的面积=3.14×
=3.14×
=3.14×5
=15.7(平方厘米);
(2)因为a2=20平方厘米,
则小正方形的面积是20÷2=10(平方厘米).
答:圆的面积是15.7平方厘米,小正方形的面积是10平方厘米.
故答案为:15.7、10.
19.在一张长9厘米、宽6厘米的长方形纸上画一个尽可能大的圆,则圆规两间的距离不能超过 3 厘米;所画圆的面积是 28.26 平方厘米.
【考点】圆、圆环的面积;画圆.
【分析】根据题意,长方形内最大的圆就是以长方形宽为直径的圆;圆规两间的距离即这个圆的半径,再根据圆的面积公式求出面积.
【解答】解:长方形中最大的圆就是以宽为直径的圆,
r=6÷2=3(厘米),
3.14×32
=3.14×9
=28.26(平方厘米)
答:圆规两间的距离不能超过3厘米,所画圆的面积是28.26平方厘米.
故答案为:3,28.26.
20.如图,把一个圆分成若干等份,拼成一个近似长方形.已知长方形的宽是10厘米,长是 31.4 厘米,圆的面积是 314 平方厘米.
【考点】圆、圆环的面积.
【分析】根据圆面积的定义和拼成的图形的特点:近似长方形的长等于圆周长的一半,宽等于圆的半径,然后根据圆的面积和周长公式解答即可.
【解答】解:长方形长:3.14×10=31.4(厘米)
圆的面积:3.14×102=314(平方厘米)
答:长是31.4厘米,圆的面积是314平方厘米.
故答案为:31.4,314.
21.把一个圆分成16等份,然后剪开拼成近似的长方形(如图).已知这个近似长方形的周长为16.56厘米,这个圆的面积是 12.56 平方厘米.
【考点】圆、圆环的面积.
【分析】把一个圆形纸片剪开后,拼成一个宽等于半径、面积不变的近似长方形.这个近似长方形的长就是圆周长的一半,求出圆的半径,根据圆面积公式求出圆的面积.据此解答.
【解答】解:圆的半径是:
16.56÷2÷(1+3.14)
=16.56÷2÷4.14
=2(厘米)
圆的面积是:
3.14×22
=3.14×4
=12.56(平方厘米).
答:这个圆的面积是12.56平方厘米.
故答案为:12.56.
22.利用一张边长是10厘米的正方形纸,剪出一个最大的圆.这个圆的面积是 78.5 平方厘米,这张纸的利用率是 78.5% .
【考点】圆、圆环的面积;百分数的实际应用.
【分析】利用一张边长是10厘米的正方形纸,剪出一个最大的圆.这个圆的直径等于正方形的边长,根据圆的面积公式:s=πr2,正方形的面积公式:s=a2,分别求出圆和正方形的面积,再根据百分数的意义,用除法解答.
【解答】解:3.14×(10÷2)2÷(10×10)
=3.14×25÷100
=78.5÷100
=0.785
=78.5%.
答:这个圆的面积是78.5平方厘米,这张纸的利用率是78.5%.
故答案为:78.5,78.5%.
23.以一个圆的半径为边长的正方形的面积是10平方厘米,这个圆的面积是 31.4 平方厘米.
【考点】圆、圆环的面积.
【分析】已知正方形的面积是10平方厘米,而正方形的边长是圆的半径,从而有r2=10,根据圆的面积公式πr2就可以求出圆的面积.
【解答】解:圆的面积=πr2
=3.14×10
=31.4(平方厘米),
答:这个圆的面积是31.4平方厘米.
故答案为:31.4.
24.在一块边长是20厘米的正方形的木板上锯一个最大的圆,这个圆的面积是 314 平方厘米,剩下的边料是 86 平方厘米.
【考点】圆、圆环的面积;组合图形的面积.
【分析】根据“在一块边长是20厘米的正方形的木板上锯一个最大的圆,”可以知道圆的半径是20÷2,再根据圆的面积公式(S=πR2),列式解答即可.
【解答】解:3.14×(20÷2)2
=3.14×10×10
=314(平分厘米);
20×20﹣314,
=400﹣314,
=86(平分厘米);
答:这个圆的面积是314平方厘米,剩下的边料是86平方厘米.
故答案为:314,86.
25.圆的半径扩大到原来的3倍,面积也扩大了3倍. × .(判断对错)
【考点】圆、圆环的面积;积的变化规律.
【分析】圆的面积=π×r×r,其中π是一个定值,根据积的变化规律:一个因数不变,另一个因数扩大或缩小几倍,积就扩大或缩小几倍,即可解答.
【解答】解:圆的面积=π×r×r,r扩大3倍,则圆的面积就扩大:3×3=9倍,
所以原题说法错误.
故答案为:×.
26.在一个面积为16平方厘米的正方形内,画一个最大的圆,这个圆的面积是 12.56 平方厘米.
【考点】圆、圆环的面积.
【分析】因为4×4=16平方厘米,所以这个正方形的边长是4厘米,所以正方形内最大的圆的直径就是4厘米,由此利用圆的面积公式即可解答.
【解答】解:因为4×4=16平方厘米,所以这个正方形的边长是4厘米,
则正方形内最大的圆的直径就是4厘米,
所以这个圆的面积是:3.14×=12.56(平方厘米);
答:这个圆的面积是12.56平方厘米.
故答案为:12.56.
三、解答题(共4小题)
27.已知圆的面积是9.42平方厘米,阴影部分的面积是多少平方厘米?
【考点】圆、圆环的面积;三角形的周长和面积.
【分析】根据圆的面积公式,用圆的面积除以3.14可求出半径的平方,就是三角形两条直角边的乘积,再除以2就是阴影部分的面积,据此解答.
【解答】解:9.42÷3.14÷2
=3÷2
=1.5(平方厘米)
答:阴影部分的面积是1.5平方厘米.
28.如图,正方形的边长为2cm,求阴影部分的面积(圆周率取3.14).
【考点】圆、圆环的面积.
【分析】根据阴影部分的面积=正方形的面积﹣空白部分的面积即可得出答案,利用正方形和圆的面积公式即可求解.
【解答】解:2×2﹣3.14×(2÷2)2
=4﹣3.14
=0.86(平方厘米)
答:阴影部分的面积是0.86平方厘米.
29.已知长方形面积与圆面积相等.已知圆的半径是3厘米,求阴影部分的面积.
【考点】圆、圆环的面积.
【分析】由题意可知:长方形面积与圆面积相等,则阴影部分的面积就等于圆的面积,据此利用圆的面积公式即可求解.
【解答】解:3.14×32×
=3.14×9×
=21.195(平方厘米)
答:阴影部分的面积是21.195平方厘米.
30.小方桌的边长是1米,把它的四边撑开就成了一张圆桌(如图)求圆桌的面积.
【考点】圆、圆环的面积.
【分析】如图,连接正方形的对角线,把正方形平均分成了4个等腰直角三角形,且每一条直角边都是圆的半径;一个等腰直角三角形的面积就是正方形面积的,由于正方形的面积是1×1=1平方米,所以一个等腰直角三角形的面积就是平方米,即r2÷2=,可求得r2是,进而求得圆桌的面积.
【解答】解:连接正方形的对角线,把正方形平均分成了4个等腰直角三角形,如下图:
每一条直角边都是圆的半径;
正方形的面积:1×1=1(平方米),
小等腰直角三角形的面积就是平方米,
即:r2÷2=,r2=;
圆桌的面积:3.14×r2=3.14×=1.57(平方米);
答:圆桌的面积是1.57平方米.
一、选择题(共9小题)
1.一张长方形纸长12厘米,宽8厘米,在这张长方形的纸中剪一个最大的圆,这个圆的面积是( )平方厘米.
A.113.04 B.50.24 C.96 D.45.76
2.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形的( )
A. B. C. D.
3.圆的半径扩大2倍,圆的面积就扩大( )倍.
A.2 B.4 C.8 D.16
4.小圆的直径等于大圆的半径,小圆的面积是大圆面积的( )
A. B. C. D.
5.大圆与小圆半径的比是5:4,大圆面积与小圆面积的比是( )
A.5:4 B.10:8 C.25:16
6.一个圆环,它的外圆直径是内圆直径的2倍,这个圆环的面积( )
A.比内圆面积大 B.比内圆面积小
C.与内圆面积相等
7.小圆和大圆的半径分别是2厘米和5厘米,小圆与大圆的面积之比是( )
A.2:5 B.4:10 C.4:25 D.2:10
8.圆的半径扩大3倍,面积扩大( )
A.3倍 B.6倍 C.9倍
9.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形面积的( )
A. B. C. D.
二、填空题(共17小题)
10.大圆的直径是小圆半径的2倍,小圆的面积是大圆面积的倍. (判断对错)
11.已知圆的直径为20厘米,则圆的面积为 平方厘米.(π取3.14)
12.半圆的面积是它所在圆面积的一半. .
13.周长相等的两个圆,它们的面积也一定相等. .(判断对错)
14.在一个圆内,以它的半径为边长做一个正方形,已知正方形面积是36cm2,圆的面积是 cm2.
15.半圆的面积是这个圆的面积的一半. (判断对错)
16.从一个边长为20厘米的正方形纸片中,剪出一个最大的圆,这个圆的面积是 平方厘米.
17.周长相等的两个圆,面积不一定相等. .(判断对错)
18.如图,在一个面积是20平方厘米的正方形内画一个最大的圆,圆的面积是 平方厘米,继续在这个圆内画一个最大的正方形,画出的正方形的面积是 平方厘米.
19.在一张长9厘米、宽6厘米的长方形纸上画一个尽可能大的圆,则圆规两间的距离不能超过 厘米;所画圆的面积是 平方厘米.
20.如图,把一个圆分成若干等份,拼成一个近似长方形.已知长方形的宽是10厘米,长是 厘米,圆的面积是 平方厘米.
21.把一个圆分成16等份,然后剪开拼成近似的长方形(如图).已知这个近似长方形的周长为16.56厘米,这个圆的面积是 平方厘米.
22.利用一张边长是10厘米的正方形纸,剪出一个最大的圆.这个圆的面积是 平方厘米,这张纸的利用率是 .
23.以一个圆的半径为边长的正方形的面积是10平方厘米,这个圆的面积是 平方厘米.
24.在一块边长是20厘米的正方形的木板上锯一个最大的圆,这个圆的面积是 平方厘米,剩下的边料是 平方厘米.
25.圆的半径扩大到原来的3倍,面积也扩大了3倍. .(判断对错)
26.在一个面积为16平方厘米的正方形内,画一个最大的圆,这个圆的面积是 平方厘米.
三、解答题(共4小题)
27.已知圆的面积是9.42平方厘米,阴影部分的面积是多少平方厘米?
28.如图,正方形的边长为2cm,求阴影部分的面积(圆周率取3.14).
29.已知长方形面积与圆面积相等.已知圆的半径是3厘米,求阴影部分的面积.
30.小方桌的边长是1米,把它的四边撑开就成了一张圆桌(如图)求圆桌的面积.
青岛版六三制新六年级(上)小升初题单元试卷:五 完美的图形---圆(04)
参考答案与试题解析
一、选择题(共9小题)
1.一张长方形纸长12厘米,宽8厘米,在这张长方形的纸中剪一个最大的圆,这个圆的面积是( )平方厘米.
A.113.04 B.50.24 C.96 D.45.76
【考点】圆、圆环的面积.
【分析】在这个长方形纸上画的最大圆的直径应等于长方形的宽,长方形的宽已知,从而利用圆的面积公式:s=πr2,即可求出圆的面积.
【解答】解:这个圆的直径是8厘米;
圆的面积:3.14×(8÷2)2,
=3.14×16,
=50.24(平方厘米).
答:这个圆的面积是50.24平方厘米.
故选B.
2.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形的( )
A. B. C. D.
【考点】圆、圆环的面积;长方形、正方形的面积.
【分析】根据题意可知:这个圆的直径就是正方形的边长,再依据圆的面积公式:s=πr2即可求其面积,再利用圆的面积除以正方形的面积即可解答问题.
【解答】解:π×(6÷2)2
=π×9
=9π(平方厘米),
正方形的面积是:6×6=36(平方厘米)
所以9π÷36=,
答:圆的面积占正方形的.
故选:C.
3.圆的半径扩大2倍,圆的面积就扩大( )倍.
A.2 B.4 C.8 D.16
【考点】圆、圆环的面积.
【分析】这道题中圆的半径不是一个具体的数字,像这种情况下,我们可以采用假设法,把它的半径假设成一个具体的数,根据面积公式算出它们原来和扩大后的面积,再用除法算一算它的面积扩大多少倍.
【解答】解:假设这个圆原来的半径是1厘米,则扩大2倍后半径是2厘米
原来圆的面积S=πr2=3.14×12=3.14(平方厘米)
扩大后圆的面积S=πr2=3.14×22=12.56(平方厘米)
12.56÷3.14=4倍
故选:B.
4.小圆的直径等于大圆的半径,小圆的面积是大圆面积的( )
A. B. C. D.
【考点】圆、圆环的面积.
【分析】设小圆的直径等于大圆的半径是1,利用圆的面积公式计算出它们的面积即可解答.
【解答】解:设小圆的直径等于大圆的半径是1,则:
小圆的面积为:π=;
大圆的面积为:π×12=π;
所以小圆的面积是大圆的面积的.
故选:B.
5.大圆与小圆半径的比是5:4,大圆面积与小圆面积的比是( )
A.5:4 B.10:8 C.25:16
【考点】圆、圆环的面积.
【分析】根据大圆与小圆半径的比是5:4,可把大圆的半径看作5份数,小圆的半径看作4份数;进而根据圆的面积=πr2,分别求出大圆的面积和小圆的面积,然后根据题意,写出比值即可.
【解答】解:(π×52):(π×42)
=25π:16π
=25:16
答:大圆面积与小圆面积比是25:16.
故选:C.
6.一个圆环,它的外圆直径是内圆直径的2倍,这个圆环的面积( )
A.比内圆面积大 B.比内圆面积小
C.与内圆面积相等
【考点】圆、圆环的面积.
【分析】根据“外圆直径是内圆直径的2倍”,知道外圆半径是内圆半径的2倍,由此根据圆的面积公式S=πr2,分别用内圆的半径表示出两个圆的面积,进而得出圆环的面积,再与内圆的面积比较,从而做出选择.
【解答】解:设内圆的半径为r,则外圆的半径为2r,
所以圆环的面积是π(2r)2﹣πr2=3πr2>πr2,
所以这个圆环的面积比内圆面积大;
故选:A.
7.小圆和大圆的半径分别是2厘米和5厘米,小圆与大圆的面积之比是( )
A.2:5 B.4:10 C.4:25 D.2:10
【考点】圆、圆环的面积;比的意义.
【分析】根据圆的面积公式:S=πr2,据此求出大小圆的面积,然后求比,再根据比的基本性质化简比.
【解答】解:小圆的面积是:π×22=4π,
大圆的面积是:π×52=25π,
小圆面积和大圆面积的比是:4π:25π=4:25;
故选:C.
8.圆的半径扩大3倍,面积扩大( )
A.3倍 B.6倍 C.9倍
【考点】圆、圆环的面积.
【分析】这道题中圆的半径不是一个具体的数字,像这种情况下,我们可以采用假设法,把它的半径假设成一个具体的数,根据面积公式算出它们原来和扩大后的面积,再用除法算一算它的面积扩大多少倍即可判断.
【解答】解:假设这个圆原来的半径是1厘米,则扩大3倍后半径是3厘米,
原来圆的面积S=πr2=π×12=π(平方厘米),
扩大后圆的面积S=πr2=π×32=9π(平方厘米),
9π÷π=9倍;
答:圆的半径扩大3倍,面积扩大9倍.
故选:C.
9.在边长是6厘米的正方形内画一个最大的圆,圆的面积占正方形面积的( )
A. B. C. D.
【考点】圆、圆环的面积;分数除法应用题;长方形、正方形的面积.
【分析】根据题意可知:这个圆的直径就是正方形的边长,再依据圆的面积公式:s=πr2即可求其面积,再利用圆的面积除以正方形的面积即可解答问题.
【解答】解:π×(6÷2)2
=π×9
=9π(平方厘米),
正方形的面积是:6×6=36(平方厘米)
所以9π÷36=,
答:圆的面积占正方形的.
故选:A.
二、填空题(共17小题)
10.大圆的直径是小圆半径的2倍,小圆的面积是大圆面积的倍. × (判断对错)
【考点】圆、圆环的面积.
【分析】因为大圆的直径是小圆半径的2倍,设小圆的半径是r,大圆的直径是2r,大圆的半径是r,由此根据圆的面积公式得出小圆的面积与大圆的面积相等.
【解答】解:设小圆的半径是r,大圆的直径是2r,大圆的半径是r
所以小圆的面积与大圆的面积相等;
故答案为:×.
11.已知圆的直径为20厘米,则圆的面积为 314 平方厘米.(π取3.14)
【考点】圆、圆环的面积.
【分析】圆的面积=πr2,由此代入数据即可解答.
【解答】解:3.14×(20÷2)2
=3.14×100
=314(平方厘米)
答:圆的面积是314平方厘米.
故答案为:314.
12.半圆的面积是它所在圆面积的一半. √ .
【考点】圆、圆环的面积.
【分析】要判断对或错,通过计算即可得出答案.
【解答】解:圆的面积=πr2,
半圆的面积=πr2,
故答案为:√.
13.周长相等的两个圆,它们的面积也一定相等. √ .(判断对错)
【考点】圆、圆环的面积;圆、圆环的周长.
【分析】根据圆的周长公式、面积公式与半径的关系,可以得出结论.
【解答】解:根据圆的周长公式:C=2πr,可以得出两个圆周长相等,则它们的半径就相等;
再根据圆的面积公式:S=πr2,半径相等则面积就相等.
故答案为:√.
14.在一个圆内,以它的半径为边长做一个正方形,已知正方形面积是36cm2,圆的面积是 113.04 cm2.
【考点】圆、圆环的面积.
【分析】根据题干,设圆的半径是r,则r2=36,据此代入圆的面积=πr2中即可求出圆的面积.
【解答】解:根据题干分析可得:设圆的半径是r,则r2=36,
所以圆的面积是:3.14×36=113.04(平方厘米)
答:圆的面积是113.04平方厘米.
故答案为:113.04.
15.半圆的面积是这个圆的面积的一半. √ (判断对错)
【考点】圆、圆环的面积.
【分析】根据圆的面积公式:s=πr2,半圆的面积就是这个圆面积的一半.
【解答】解:圆的面积=πr2,
半圆的面积=πr2,
因此,半圆的面积是圆的面积的一半.此说法正确.
故答案为:√.
16.从一个边长为20厘米的正方形纸片中,剪出一个最大的圆,这个圆的面积是 314 平方厘米.
【考点】圆、圆环的面积.
【分析】由题意知,在正方形内剪出的面积最大的圆形纸片,其直径就等于正方形的边长,即20厘米;要求这个圆形的面积,可利用圆面积公式S=πr2求得即可.
【解答】解:3.14×(20÷2)2
=3.14×100
=314(平方厘米).
答:这个圆的面积是314平方厘米.
故答案为:314.
17.周长相等的两个圆,面积不一定相等. × .(判断对错)
【考点】圆、圆环的面积;圆、圆环的周长.
【分析】因为两个圆周长相等,周长公式:c=2πr,因为圆周率是一定的,所以两个圆的半径相等,根据圆的面积公式S=πr2,两个圆的面积一定相等.
【解答】解:因为圆周率是一定的,两个圆的周长相等,即半径相等,所以它们的面积一定相等.
故答案为:×.
18.如图,在一个面积是20平方厘米的正方形内画一个最大的圆,圆的面积是 15.7 平方厘米,继续在这个圆内画一个最大的正方形,画出的正方形的面积是 10 平方厘米.
【考点】圆、圆环的面积;长方形、正方形的面积.
【分析】由题意可知:这个最大圆的直径应该等于大正方形的边长,据此利用圆的面积公式即可求出圆的面积;小正方形的对角线等于圆的直径,则小正方形的面积对角线的平方的2倍,据此解答即可.
【解答】解:(1)设正方形的边长为a,圆的半径为,
则a2=20平方厘米,
圆的面积=3.14×
=3.14×
=3.14×5
=15.7(平方厘米);
(2)因为a2=20平方厘米,
则小正方形的面积是20÷2=10(平方厘米).
答:圆的面积是15.7平方厘米,小正方形的面积是10平方厘米.
故答案为:15.7、10.
19.在一张长9厘米、宽6厘米的长方形纸上画一个尽可能大的圆,则圆规两间的距离不能超过 3 厘米;所画圆的面积是 28.26 平方厘米.
【考点】圆、圆环的面积;画圆.
【分析】根据题意,长方形内最大的圆就是以长方形宽为直径的圆;圆规两间的距离即这个圆的半径,再根据圆的面积公式求出面积.
【解答】解:长方形中最大的圆就是以宽为直径的圆,
r=6÷2=3(厘米),
3.14×32
=3.14×9
=28.26(平方厘米)
答:圆规两间的距离不能超过3厘米,所画圆的面积是28.26平方厘米.
故答案为:3,28.26.
20.如图,把一个圆分成若干等份,拼成一个近似长方形.已知长方形的宽是10厘米,长是 31.4 厘米,圆的面积是 314 平方厘米.
【考点】圆、圆环的面积.
【分析】根据圆面积的定义和拼成的图形的特点:近似长方形的长等于圆周长的一半,宽等于圆的半径,然后根据圆的面积和周长公式解答即可.
【解答】解:长方形长:3.14×10=31.4(厘米)
圆的面积:3.14×102=314(平方厘米)
答:长是31.4厘米,圆的面积是314平方厘米.
故答案为:31.4,314.
21.把一个圆分成16等份,然后剪开拼成近似的长方形(如图).已知这个近似长方形的周长为16.56厘米,这个圆的面积是 12.56 平方厘米.
【考点】圆、圆环的面积.
【分析】把一个圆形纸片剪开后,拼成一个宽等于半径、面积不变的近似长方形.这个近似长方形的长就是圆周长的一半,求出圆的半径,根据圆面积公式求出圆的面积.据此解答.
【解答】解:圆的半径是:
16.56÷2÷(1+3.14)
=16.56÷2÷4.14
=2(厘米)
圆的面积是:
3.14×22
=3.14×4
=12.56(平方厘米).
答:这个圆的面积是12.56平方厘米.
故答案为:12.56.
22.利用一张边长是10厘米的正方形纸,剪出一个最大的圆.这个圆的面积是 78.5 平方厘米,这张纸的利用率是 78.5% .
【考点】圆、圆环的面积;百分数的实际应用.
【分析】利用一张边长是10厘米的正方形纸,剪出一个最大的圆.这个圆的直径等于正方形的边长,根据圆的面积公式:s=πr2,正方形的面积公式:s=a2,分别求出圆和正方形的面积,再根据百分数的意义,用除法解答.
【解答】解:3.14×(10÷2)2÷(10×10)
=3.14×25÷100
=78.5÷100
=0.785
=78.5%.
答:这个圆的面积是78.5平方厘米,这张纸的利用率是78.5%.
故答案为:78.5,78.5%.
23.以一个圆的半径为边长的正方形的面积是10平方厘米,这个圆的面积是 31.4 平方厘米.
【考点】圆、圆环的面积.
【分析】已知正方形的面积是10平方厘米,而正方形的边长是圆的半径,从而有r2=10,根据圆的面积公式πr2就可以求出圆的面积.
【解答】解:圆的面积=πr2
=3.14×10
=31.4(平方厘米),
答:这个圆的面积是31.4平方厘米.
故答案为:31.4.
24.在一块边长是20厘米的正方形的木板上锯一个最大的圆,这个圆的面积是 314 平方厘米,剩下的边料是 86 平方厘米.
【考点】圆、圆环的面积;组合图形的面积.
【分析】根据“在一块边长是20厘米的正方形的木板上锯一个最大的圆,”可以知道圆的半径是20÷2,再根据圆的面积公式(S=πR2),列式解答即可.
【解答】解:3.14×(20÷2)2
=3.14×10×10
=314(平分厘米);
20×20﹣314,
=400﹣314,
=86(平分厘米);
答:这个圆的面积是314平方厘米,剩下的边料是86平方厘米.
故答案为:314,86.
25.圆的半径扩大到原来的3倍,面积也扩大了3倍. × .(判断对错)
【考点】圆、圆环的面积;积的变化规律.
【分析】圆的面积=π×r×r,其中π是一个定值,根据积的变化规律:一个因数不变,另一个因数扩大或缩小几倍,积就扩大或缩小几倍,即可解答.
【解答】解:圆的面积=π×r×r,r扩大3倍,则圆的面积就扩大:3×3=9倍,
所以原题说法错误.
故答案为:×.
26.在一个面积为16平方厘米的正方形内,画一个最大的圆,这个圆的面积是 12.56 平方厘米.
【考点】圆、圆环的面积.
【分析】因为4×4=16平方厘米,所以这个正方形的边长是4厘米,所以正方形内最大的圆的直径就是4厘米,由此利用圆的面积公式即可解答.
【解答】解:因为4×4=16平方厘米,所以这个正方形的边长是4厘米,
则正方形内最大的圆的直径就是4厘米,
所以这个圆的面积是:3.14×=12.56(平方厘米);
答:这个圆的面积是12.56平方厘米.
故答案为:12.56.
三、解答题(共4小题)
27.已知圆的面积是9.42平方厘米,阴影部分的面积是多少平方厘米?
【考点】圆、圆环的面积;三角形的周长和面积.
【分析】根据圆的面积公式,用圆的面积除以3.14可求出半径的平方,就是三角形两条直角边的乘积,再除以2就是阴影部分的面积,据此解答.
【解答】解:9.42÷3.14÷2
=3÷2
=1.5(平方厘米)
答:阴影部分的面积是1.5平方厘米.
28.如图,正方形的边长为2cm,求阴影部分的面积(圆周率取3.14).
【考点】圆、圆环的面积.
【分析】根据阴影部分的面积=正方形的面积﹣空白部分的面积即可得出答案,利用正方形和圆的面积公式即可求解.
【解答】解:2×2﹣3.14×(2÷2)2
=4﹣3.14
=0.86(平方厘米)
答:阴影部分的面积是0.86平方厘米.
29.已知长方形面积与圆面积相等.已知圆的半径是3厘米,求阴影部分的面积.
【考点】圆、圆环的面积.
【分析】由题意可知:长方形面积与圆面积相等,则阴影部分的面积就等于圆的面积,据此利用圆的面积公式即可求解.
【解答】解:3.14×32×
=3.14×9×
=21.195(平方厘米)
答:阴影部分的面积是21.195平方厘米.
30.小方桌的边长是1米,把它的四边撑开就成了一张圆桌(如图)求圆桌的面积.
【考点】圆、圆环的面积.
【分析】如图,连接正方形的对角线,把正方形平均分成了4个等腰直角三角形,且每一条直角边都是圆的半径;一个等腰直角三角形的面积就是正方形面积的,由于正方形的面积是1×1=1平方米,所以一个等腰直角三角形的面积就是平方米,即r2÷2=,可求得r2是,进而求得圆桌的面积.
【解答】解:连接正方形的对角线,把正方形平均分成了4个等腰直角三角形,如下图:
每一条直角边都是圆的半径;
正方形的面积:1×1=1(平方米),
小等腰直角三角形的面积就是平方米,
即:r2÷2=,r2=;
圆桌的面积:3.14×r2=3.14×=1.57(平方米);
答:圆桌的面积是1.57平方米.
