2.2 命题与证明同步测试（含答案）

第二章第二节《命题与证明》同步测试
一．选择题（共10小题）
1．下列命题中，是假命题的是（　　）
　
A．
对顶角相等
B．
同旁内角互补
　
C．
两点确定一条直线
D．
角平分线上的点到这个角的两边的距离相等
　
2．下列命题的逆命题一定成立的是（　　）
①对顶角相等；
②同位角相等，两直线平行；
③若a=b，则|a|=|b|；
④若x=3，则x2﹣3x=0．
　
A．①②③
B．
①④
C．
②④
D．
②
　
3．如图所示，①代表0，②代表9，③代表6，则④代表（　　）
　
A．1
B．
3
C．
5
D．
7
　
4．下列命题是真命题的是（　　）
　
A．
任何数的0次幂都等于1
　
B．
顺次连接菱形四边中点的线段组成的四边形是正方形
　
C．
图形的旋转和平移会改变图形的形状和大小
　
D．
角平分线上的点到角两边的距离相等
　
5．下列语句中，属于定义的是（　　）
　
A．
两点确定一条直线
B．
平行线的同位角相等
　
C．
两点之间线段最短
D．
直线外一点到直线的垂线段的长度，叫做点到直线的距离
　
6．为了证明命题“任何偶数都是8的整数倍”是假命题，下列各数中可以作为反例的是（　　）
　
A．32
B．
16
C．
8
D．
4
　
7．下列选项中，可以用来证明命题“若|a﹣1|＞1，则a＞2”是假命题的反例是（　　）
　
A．a=2
B．
a=1
C．
a=0
D．
a=﹣1
　
8．命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等．其中假命题有（　　）
　
A．1个
B．
2个
C．
3个
D．
4个
　
9．要说明“若两个单项式的次数相同，则它们是同类项”是假命题，可以举的反例是（　　）
　
A．2ab和3ab
B．
2a2b和3ab2
C．
2ab和2a2b2
D．
2a3和﹣2a3
　
10．用反证法证明“a＜b”时第一步应假设（　　）
　
A．a＞b
B．
a≤b
C．
a≥b
D．
a≠b
　
　
二．填空题（共10小题）
11．要证明一个三角形中不可能有两个钝角，采用的方法是　　　　　　，应先假设　　　　　　．
　
12．有5名新同学，如果每两个人都握手1次，那么他们握手的总次数是　　　　　　次．
　
13．已知三条不同的直线a、b、c在同一平面内，下列四条命题：
①如果a∥b，a⊥c，那么b⊥c；
②如果b∥a，c∥a，那么b∥c；
③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．
其中真命题的是　　　　　　．（填写所有真命题的序号）
　
14．命题“全等三角形的面积相等”的逆命题是　　　　　　命题．（填入“真”或“假”）
　
15．命题“同位角相等，两直线平行”中，条件是　　　　　　，结论是　　　　　　
　
16．命题“角平分线上的点到角的两边的距离相等”的逆命题是　　　　　　．
　
17．改写命题“对角线互相平分的四边形是平行四边形”：如果　　　　　　，那么　　　　　　．
　
18．请举反例说明“对于任意实数x，x2+5x+4的值总是正数”是假命题，你举的反例
是x=　　　　　　（写出一个x的值即可）．
　
19．命题：“同角的余角相等”的逆命题是　　　　
　　．
　
20．将命题“过一点有且只有一条直线与已知直线垂直”改写“如果…那么…”的形式　　　
　　　．
　
三．解答题（共7小题）
21．如图，直线AB和直线CD、直线BE和直线CF都被直线BC所截．在下面三个式子中，请你选择其中两个作为题设，剩下的一个作为结论，组成一个真命题并证明．
①AB⊥BC、CD⊥BC，②BE∥CF，③∠1=∠2．
题设（已知）：　　　　　　．
结论（求证）：　　　　　　．
证明：　　　　　　．
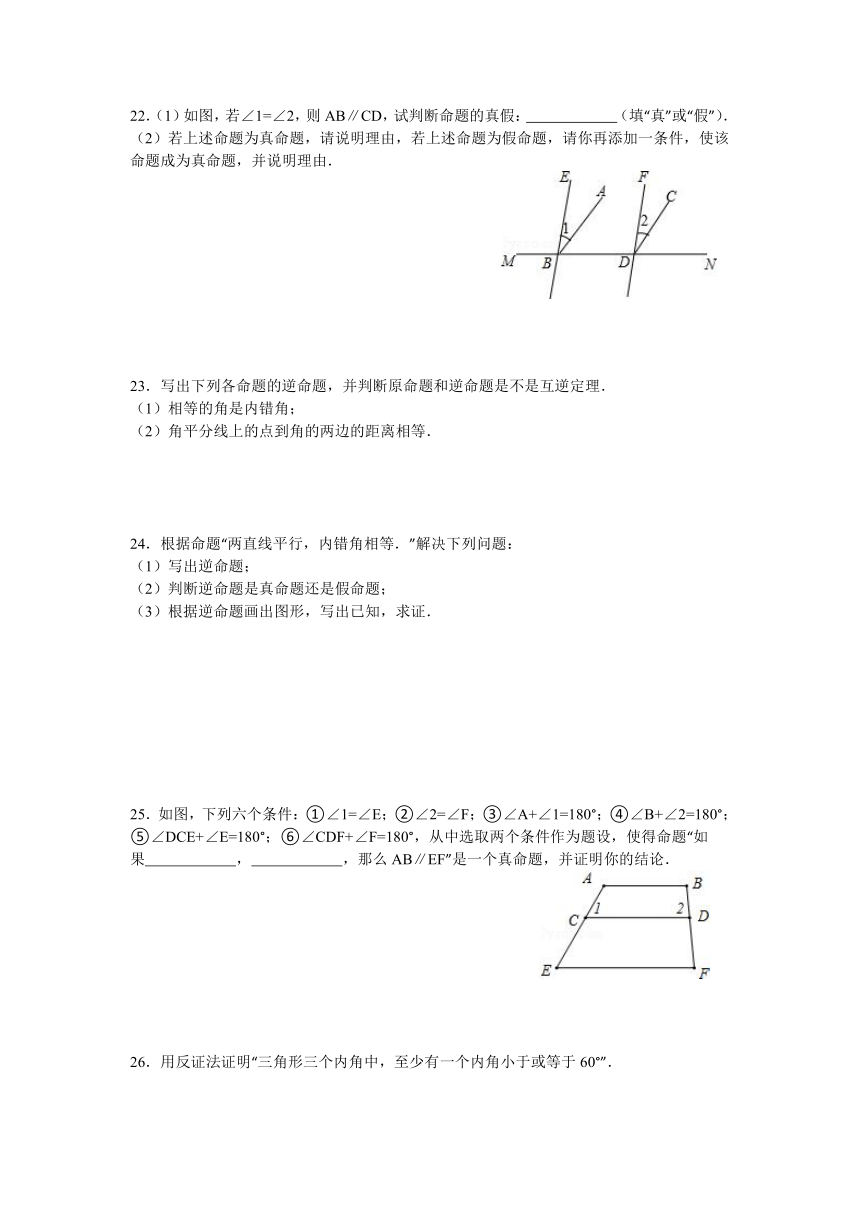
22．（1）如图，若∠1=∠2，则AB∥CD，试判断命题的真假：　　　　　　（填“真”或“假”）．
（2）若上述命题为真命题，请说明理由，若上述命题为假命题，请你再添加一条件，使该命题成为真命题，并说明理由．
　
23．写出下列各命题的逆命题，并判断原命题和逆命题是不是互逆定理．
（1）相等的角是内错角；
（2）角平分线上的点到角的两边的距离相等．
　
24．根据命题“两直线平行，内错角相等．”解决下列问题：
（1）写出逆命题；
（2）判断逆命题是真命题还是假命题；
（3）根据逆命题画出图形，写出已知，求证．
　
25．如图，下列六个条件：①∠1=∠E；②∠2=∠F；③∠A+∠1=180°；④∠B+∠2=180°；⑤∠DCE+∠E=180°；⑥∠CDF+∠F=180°，从中选取两个条件作为题设，使得命题“如果　　　　　　，　　　　　　，那么AB∥EF”是一个真命题，并证明你的结论．
　
26．用反证法证明“三角形三个内角中，至少有一个内角小于或等于60°”．
已知：∠A，∠B，∠C是△ABC的内角．求证：∠A，∠B，∠C中至少有一个内角小于或等于60°．
证明：假设求证的结论不成立，那么　　　　　　
∴∠A+∠B+∠C＞　　　　　　
这与三角形　　　　　　相矛盾．
∴假设不成立
∴　　　　　　．
　
27．用反证法证明（填空）：
两条直线被第三条直线所截．如果同旁内角互补，那么这两条直线平行．
已知：如图，直线l1，l2被l3所截，∠1+∠2=180°．
求证：l1　　　　　　l2
证明：假设l1　　　　　　l2，即l1与l2交与相交于一点P．
则∠1+∠2+∠P　　　　　　180°　　　　　　
所以∠1+∠2　　　　　　180°，这与　　　　　　矛盾，故　　　　　　不成立．
所以　　　　　　．
　
　
第二章第二节《命题与证明》同步测试
参考答案：
　
一．选择题（共10小题）
1．B
2.D
3.B
4.D
5.D
6.D
7.D
8.C
9.B
10.C　
二．填空题（共10小题）
11．　反证法　，
　一个三角形的三个内角中有两个角是钝角　．
　
12．　10　．
　
13．　①②④　．（填写所有真命题的序号）
　
14．　假　（填入“真”或“假”）
　
15．　同位角相等　，
　两直线平行　
　
16．　到角的两边的距离相等的是角平分线上的点　．
　
17．　四边形的对角线互相平分　，
　这个四边形是平行四边形　．
　
18．
　﹣4　（写出一个x的值即可）．
　
19．　如果两个角相等，那么这两个角是同一个角的余角　．
　
20．　如果直线外有一点，那么过这一点有且只有一条直线与已知直线垂直　．
　
三．解答题（共7小题）
21．已知：如图，AB⊥BC、CD⊥BC，BE∥CF．
求证：∠1=∠2．
证明：∵AB⊥BC、CD⊥BC，
∴AB∥CD，
∴∠ABC=∠DCB，
又∵BE∥CF，
∴∠EBC=∠FCB，
∴∠ABC﹣∠EBC=∠DCB﹣∠FCB，
∴∠1=∠2．
故答案为①②；③；省略．
22．解：（1）若∠1=∠2，则AB∥CD，是假命题；
故答案为：假；
（2）加条件：BE∥FD，
∴∠EBD=∠FDN，
又∵∠1=∠2，
∴∠ABD=∠CDN，
∴AB∥CD．
　
23．解：（1）“相等的角是内错角”的逆命题为“内错角相等”，原命题与逆命题都是假命题，不是互逆定理；
（2）“角平分线上的点到角的两边的距离相等”的逆命题为“到一个角的两边的距离相等的点在这个角的角平分线上”，原命题和逆命题是互逆定理．
　
24．解：（1）逆命题：内错角相等，两直线平行；
（2）是真命题；
（3）已知：如图，∠AMN=∠DNM，
求证：AB∥CD．
25．解：如果∠1=∠E，∠B+∠2=180°，那么AB∥EF，
∵∠1=∠E，∠B+∠2=180°，
∴CD∥EF，AB∥CD，
∴AB∥EF；
故答案为：
∠1=∠E，∠B+∠2=180°．
26．证明：假设求证的结论不成立，那么三角形中所有角都大于60°，
∴∠A+∠B+∠C＞180°，
这与三角形的三内角和为180°相矛盾．
∴假设不成立，
∴三角形三内角中至少有一个内角小于或等于60度．
故答案为：三角形中所有角都大于60°；180°；的三内角和为180°；三角形三内角中至少有一个内角小于或等于60度．
　
27．用反证法证明（填空）：
两条直线被第三条直线所截．如果同旁内角互补，那么这两条直线平行．
已知：如图，直线l1，l2被l3所截，∠1+∠2=180°．
求证：l1　∥　l2
证明：假设l1　不平行　l2，即l1与l2交与相交于一点P．
则∠1+∠2+∠P　=　180°　（三角形内角和定理）　
所以∠1+∠2　＜　180°，这与　已知　矛盾，故　假设　不成立．
所以　l1∥l2　．
证明：假设l1不平行l2，即l1与l2交与相交于一点P．
则∠1+∠2+∠P=180°（三角形内角和定理），
所以∠1+∠2＜180°，
这与∠1+∠2=180°矛盾，故假设不成立．
所以结论成立，l1∥l2．