2.5 全等三角形同步测试(含答案)
图片预览


文档简介
第二章第五节《全等三角形》同步测试
一.选择题(共13小题)
1.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N
B.AM=CN
C.AB=CD
D.AM∥CN
2.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
A.4个
B.3个
C.2个
D.1个
3.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A.1处
B.2处
C.3处
D.4处
4.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
5.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
7.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
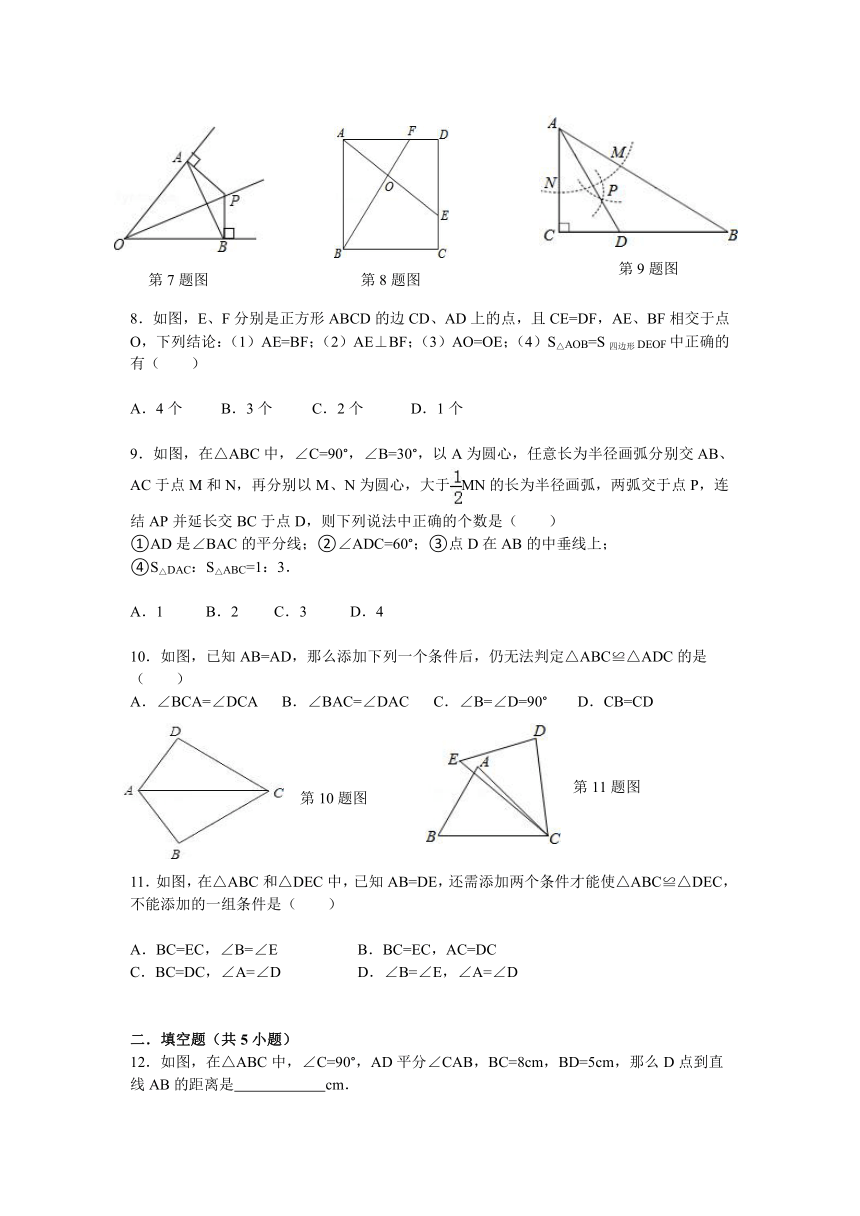
8.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个
B.3个
C.2个
D.1个
9.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;
④S△DAC:S△ABC=1:3.
A.1
B.2
C.3
D.4
10.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.∠BCA=∠DCA
B.∠BAC=∠DAC
C.∠B=∠D=90°
D.CB=CD
11.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
二.填空题(共5小题)
12.如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是 cm.
13.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).
14.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .
15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是 .
16.如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 .(答案不唯一,只需填一个)
三.解答题(共6小题)
17.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
18.(2007 乐山)如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.
19.已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.
20.如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;
(2)BO=DO.
21.如图,AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
22.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数?
第二章第五节《全等三角形》同步测试
参考答案:
一.选择题(共11小题)
1.B
2.B
3.D
4.B
5.D
6.C
7.D
8.B
9.D
10.A
11.C
二.填空题(共5小题)
12. 3
13. ∠B=∠C或AE=AD (添加一个条件即可).
14. 5 .
15. ∠ACB=∠DBC(或AB=CD) .
16. AC=CD .(答案不唯一,只需填一个)
三.解答题(共6小题)
17.
证明:∵BE=FC,
∴BE+EF=CF+EF,
即BF=CE;
又∵AB=DC,∠B=∠C,
∴△ABF≌△DCE;(SAS)
∴∠A=∠D.
18.(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE;
(2)解:
∵(1)△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
19.证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,,
∴△ABC≌△CED.
∴AC=CD.
20.证明:(1)在△ABC和△ADC中,
,
∴△ABC≌△ADC(ASA);
(2)∵△ABC≌△ADC,
∴AB=AD.
又∵∠1=∠2,AO=AO,
即,
∴△ABO≌△ADO(SAS).
∴BO=DO.
21.证明:∵在△ODC和△OBA中,
∵,
∴△ODC≌△OBA(SAS),
∴∠C=∠A(或者∠D=∠B)(全等三角形对应角相等),
∴DC∥AB(内错角相等,两直线平行).
22.(1)证明:∵在△ABE和△DCE中
∴△ABE≌△DCE(AAS);
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
第2题图
第1题图
第3题图
第4题图
第6题图
第9题图
第8题图
第7题图
第11题图
第10题图
第14题图
第12题图
第13题图
第16题图
第15题图
一.选择题(共13小题)
1.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N
B.AM=CN
C.AB=CD
D.AM∥CN
2.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
A.4个
B.3个
C.2个
D.1个
3.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有( )
A.1处
B.2处
C.3处
D.4处
4.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
5.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
7.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
8.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个
B.3个
C.2个
D.1个
9.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;
④S△DAC:S△ABC=1:3.
A.1
B.2
C.3
D.4
10.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.∠BCA=∠DCA
B.∠BAC=∠DAC
C.∠B=∠D=90°
D.CB=CD
11.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
二.填空题(共5小题)
12.如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是 cm.
13.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).
14.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .
15.如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是 .
16.如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 .(答案不唯一,只需填一个)
三.解答题(共6小题)
17.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
18.(2007 乐山)如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.
19.已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.
20.如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;
(2)BO=DO.
21.如图,AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
22.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数?
第二章第五节《全等三角形》同步测试
参考答案:
一.选择题(共11小题)
1.B
2.B
3.D
4.B
5.D
6.C
7.D
8.B
9.D
10.A
11.C
二.填空题(共5小题)
12. 3
13. ∠B=∠C或AE=AD (添加一个条件即可).
14. 5 .
15. ∠ACB=∠DBC(或AB=CD) .
16. AC=CD .(答案不唯一,只需填一个)
三.解答题(共6小题)
17.
证明:∵BE=FC,
∴BE+EF=CF+EF,
即BF=CE;
又∵AB=DC,∠B=∠C,
∴△ABF≌△DCE;(SAS)
∴∠A=∠D.
18.(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE;
(2)解:
∵(1)△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
19.证明:∵AB∥ED,
∴∠B=∠E.
在△ABC和△CED中,,
∴△ABC≌△CED.
∴AC=CD.
20.证明:(1)在△ABC和△ADC中,
,
∴△ABC≌△ADC(ASA);
(2)∵△ABC≌△ADC,
∴AB=AD.
又∵∠1=∠2,AO=AO,
即,
∴△ABO≌△ADO(SAS).
∴BO=DO.
21.证明:∵在△ODC和△OBA中,
∵,
∴△ODC≌△OBA(SAS),
∴∠C=∠A(或者∠D=∠B)(全等三角形对应角相等),
∴DC∥AB(内错角相等,两直线平行).
22.(1)证明:∵在△ABE和△DCE中
∴△ABE≌△DCE(AAS);
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
第2题图
第1题图
第3题图
第4题图
第6题图
第9题图
第8题图
第7题图
第11题图
第10题图
第14题图
第12题图
第13题图
第16题图
第15题图
同课章节目录
