锐角三角函数复习课件

课件12张PPT。九年级数学(上)第四章 2007年 11月锐角三角形函数
小结与复习(一)学习目标1.熟练掌握锐角三角函数的定义以及互余两个角的三角
函数的关系.
2.熟记特殊锐角三角函数值,即30?,45?,60?的三角函数值.
3.通过把所学的锐角三角函数知识条理化,系统化,加强对
所学知识的认识.重点:理解锐角三角函数的有关知识,并能正确运用.
难点:灵活运用锐角三角函数的有关知识.阅读 读教材P121~122《小结与复习》的第
一部分，要求：
1、记住锐角三角函数的定义和特殊锐
角的三角函数值；
2、理解并记住同一锐角的正弦、余弦
和正切之间的关系（平方关系和商式关
系）；
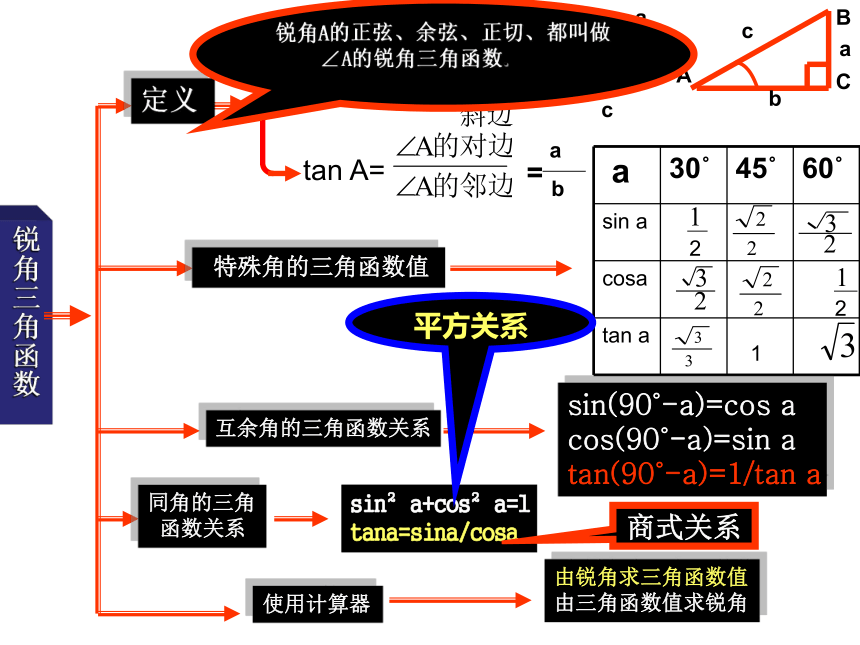
3、掌握互为余角的正弦、余弦的关系。锐角三角函数cos A= tan A= sin A= sin(90?-a)=cos a
cos(90?-a)=sin a
tan(90?-a)=1/tan asin2a+cos2a=1
tana=sina/cosa由锐角求三角函数值
由三角函数值求锐角1平方关系商式关系锐角A的正弦、余弦、正切、都叫做∠A的锐角三角函数.
1.计算cos30?tan30?+sin60?tan60?= .
2.已知tanA－1=0,2cosB－1=0,
则锐角A,B的和是 .
3.在Rt?ABC中,∠C=90°,sinA=3/5,
则cosB= ______.
4.比较大小:sin35° cos35°.
5. tan44°tan45°tan46°= .
6.若cosa=sin34°,则锐角a= .
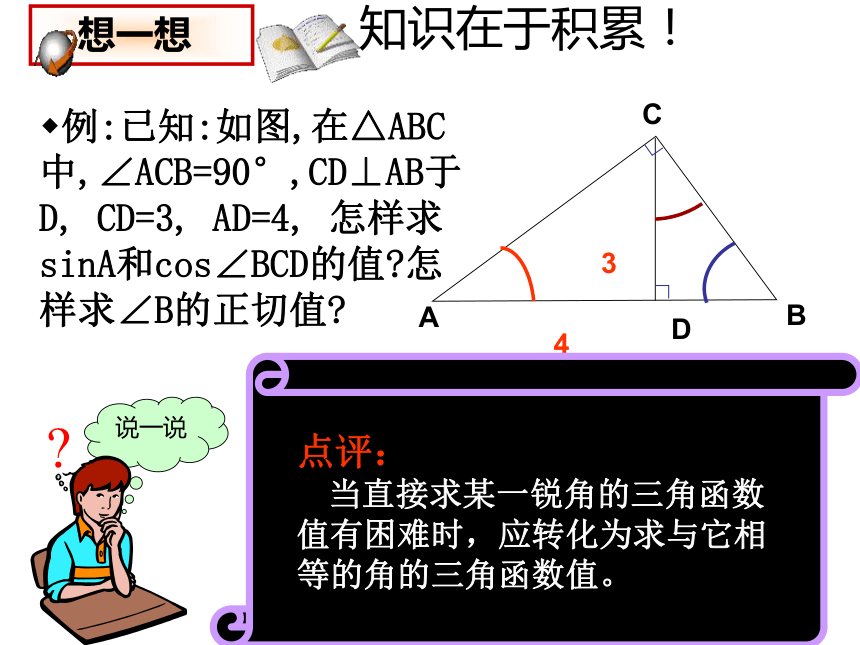
7.若a为锐角,sina=4/5,则cosa= .自主演练迎接挑战2105?3/5<156°3/5挑战成功了吗？知识在于积累！例:已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D, CD=3, AD=4, 怎样求sinA和cos∠BCD的值?怎样求∠B的正切值?说一说34解:∵在Rt△ADC中,CD=3,AD=4∵∠ACB=90°,CD⊥AB∴∠BCD+∠B=90°,∠A+∠B=90°∠ACD+∠BCD= 90° ∴∠BCD=∠A ∠B=∠ACD∴sinA=3/5 cos∠BCD=cosA=4/5tanB=tan∠ACD=AD/CD=4/3点评：
当直接求某一锐角的三角函数值有困难时，应转化为求与它相等的角的三角函数值。谁是英雄?!2.在Rt△ABC中, ∠C=90?,AB=12cm,BC=10cm,求角Ａ，Ｂ
的正弦，余弦及正切值．1.计算：1－２sin230?= , sin30?/cos30?= ,
sin45?cos30?－cos45?sin30?= .3.已知sina=2/3,a为锐角,求cosa,tana的值.谁是英雄?!4.已知tanβ=1/2, β为锐角,求sin β,cos β 的值.3.已知sina=2/3,a为锐角,求cosa,tana的值.4.已知tanβ=1/2, β为锐角,
求sin β,cos β 的值.点评:像3、4题一类的题型，已知一锐角的某种
三角函数值，可先构建直角三角形，根据已知条
件引入辅助未知数k（k>0 ），将各边用含有k的
代数式表示出来，然后根据锐角三角函数的定义
来求。小结 通过我们这一节课的探索与学习，你一定有好多的收获，你能把这些知识点加以收集与总结吗？ 1.sin2a+sin242?=1,则锐角a为 ( )
A 42? B 48? C 90? D不能确定
2.已知sina+cosa=m,sinacosa=n，则（　）
A m=n B m=2n+1 C m2=2n+1 D m2=1-2n
3.计算sin53?cos37?+cos53?sin37?的结果是（　）
A 1 B 2 C 0 D 不能确定
4.已知　　　　　　＝２，则tanβ的值为　（　）
A 2 B -2 C 4 D -43sinβ+2cosβ2sinβ－cosβ拓展与延伸BCAC你挑战成功了吗?比一比,看谁最先做出来!知识的升华必做:
P123 复习题四Ａ 2,４,８题驶向胜利的彼岸祝你成功！选做：
　已知:tana=2,则 = ,
5sinacosa－2= .　sin2a－3cos2a2sin2a+cos2a结束寄语:悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.再见