3.4 相似三角形的判定 专项练习(含答案)
文档属性
| 名称 | 3.4 相似三角形的判定 专项练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-01 00:00:00 | ||
图片预览


文档简介
3.4
相似三角形的判定
解答题专项练习
一.解答题(共12小题)
1.如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
2.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
3.如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
4.如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
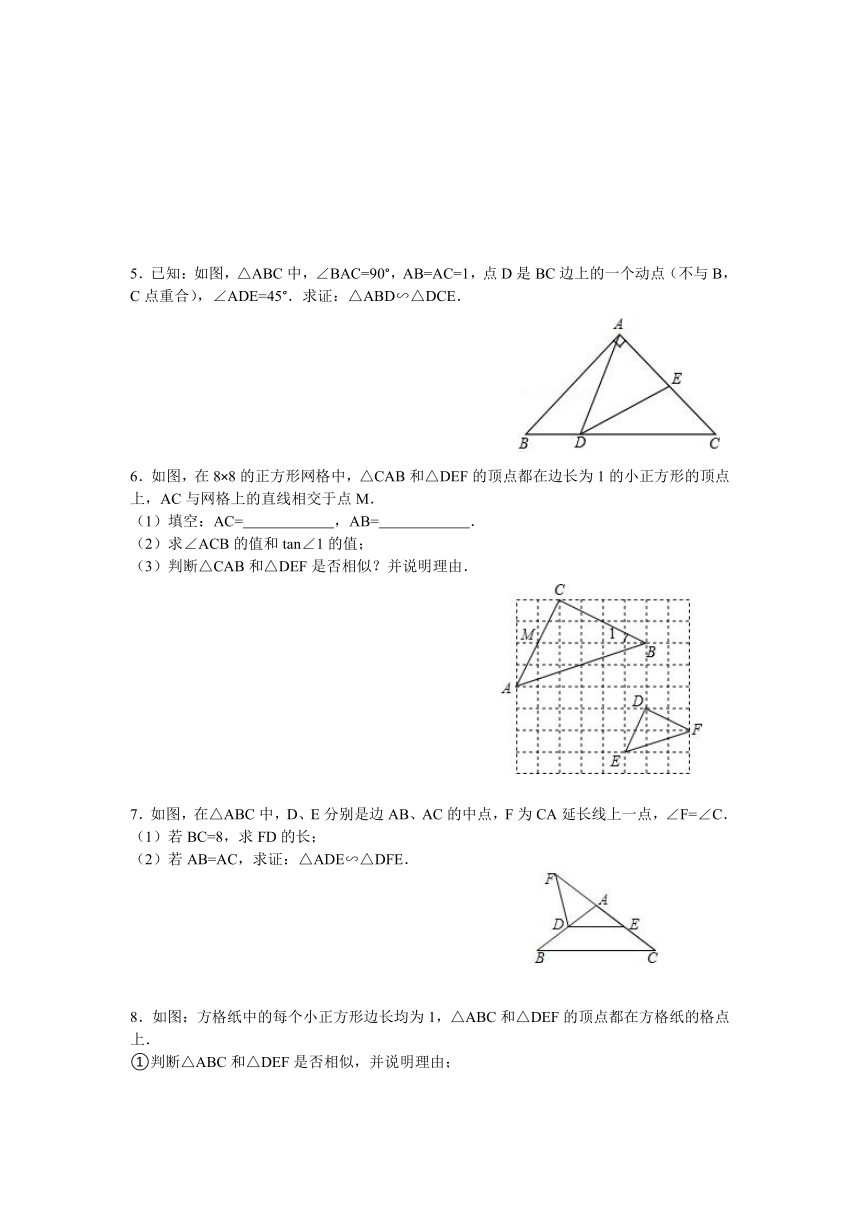
5.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
6.如图,在8×8的正方形网格中,△CAB和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.
(1)填空:AC= ,AB= .
(2)求∠ACB的值和tan∠1的值;
(3)判断△CAB和△DEF是否相似?并说明理由.
7.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.
(1)若BC=8,求FD的长;
(2)若AB=AC,求证:△ADE∽△DFE.
8.如图:方格纸中的每个小正方形边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.
①判断△ABC和△DEF是否相似,并说明理由;
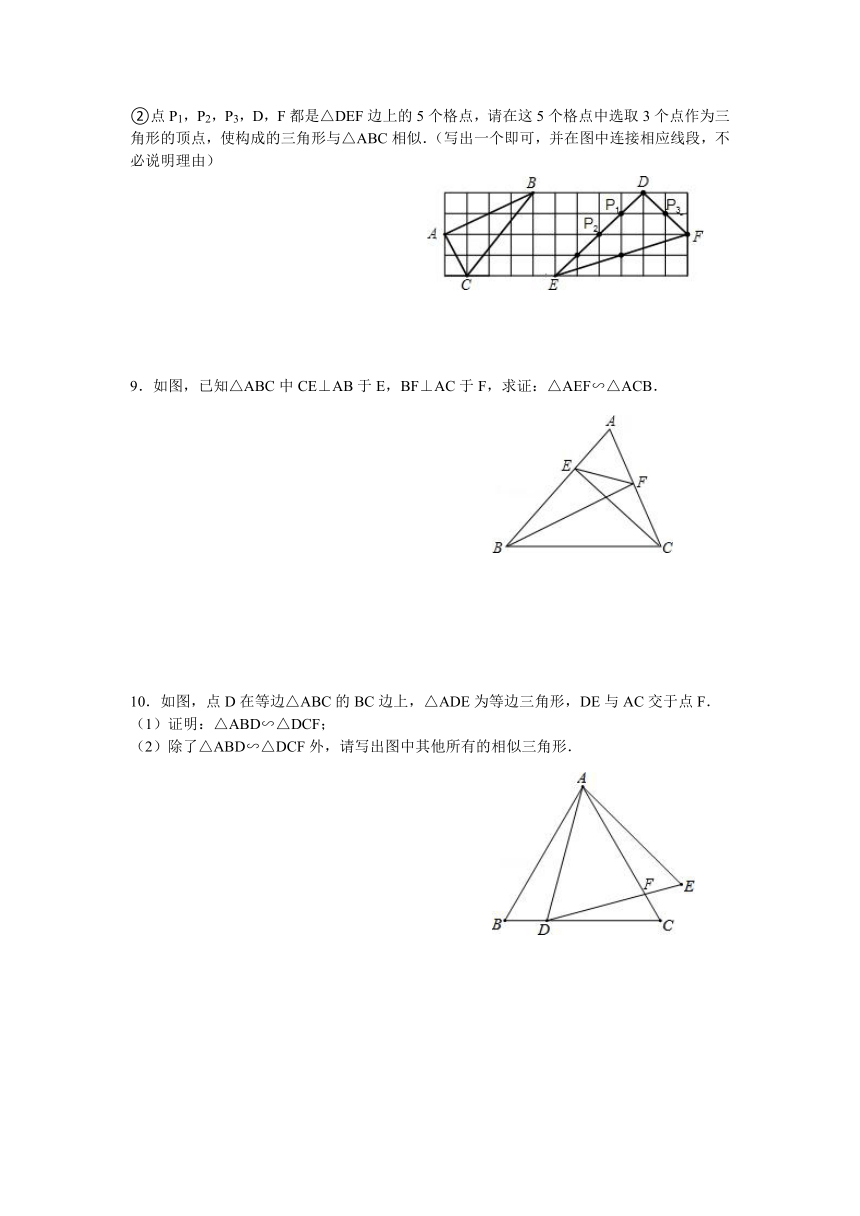
②点P1,P2,P3,D,F都是△DEF边上的5个格点,请在这5个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似.(写出一个即可,并在图中连接相应线段,不必说明理由)
9.如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,求证:△AEF∽△ACB.
10.如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
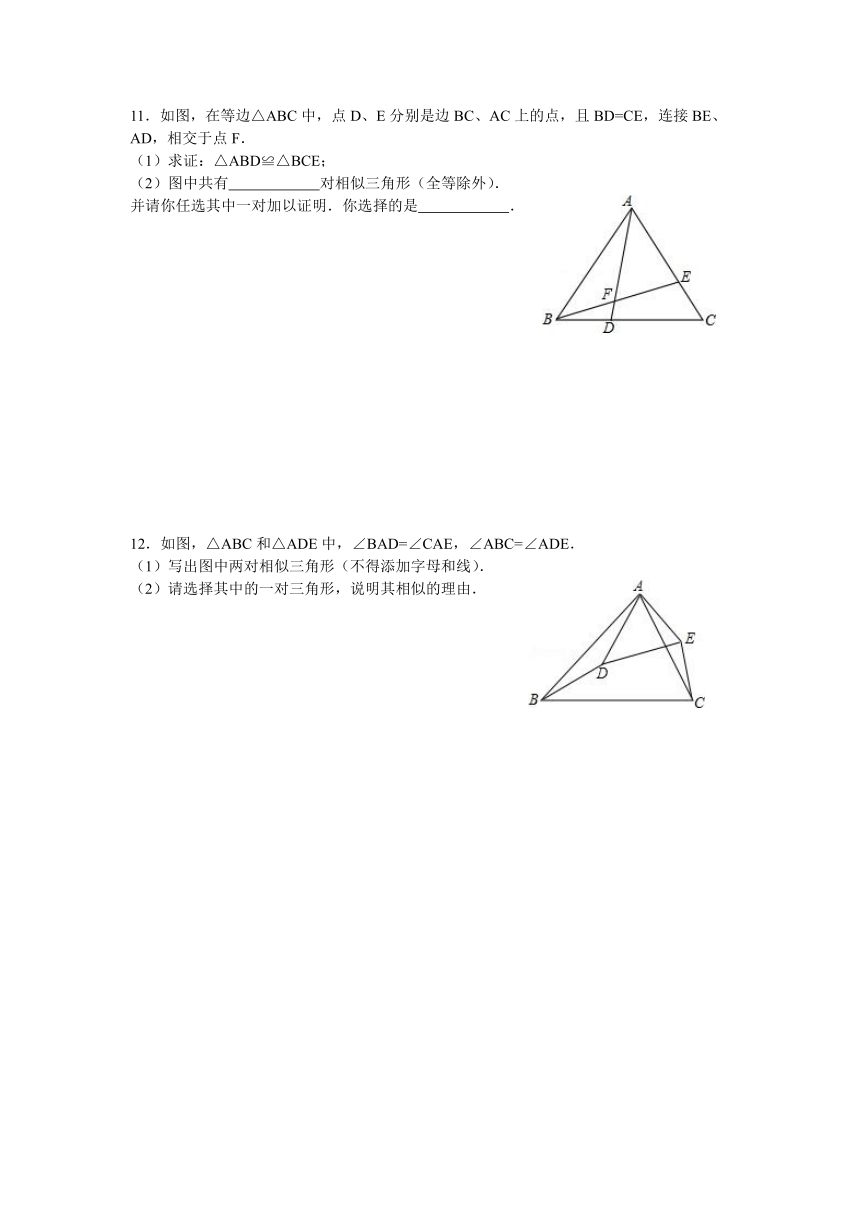
11.如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.
(1)求证:△ABD≌△BCE;
(2)图中共有 对相似三角形(全等除外).
并请你任选其中一对加以证明.你选择的是 .
12.如图,△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线).
(2)请选择其中的一对三角形,说明其相似的理由.
3.4
相似三角形的判定
解答题专项练习
参考答案与解析
一.解答题(共12小题)
1.解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠ABD=∠ABC=36°=∠A,
在△ADE和△BDE中
∵,
∴△ADE≌△BDE(AAS);
证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠DBC=∠ABC=36°=∠A,
∵∠C=∠C,
∴△ABC∽△BCD.
2.(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴,
∵DF=DC,
∴,
∴,
∴△ABE∽△DEF;
(2)解:∵ABCD为正方形,
∴ED∥BG,
∴,
又∵DF=DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.
3.解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,
∴MN=3;
②图2,作∠ANM=∠B,则△ANM∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,AC=,
∴MN=,
∴MN的长为3或.
4.证明:∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∴∠FAE+∠AFE=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠BFD=90°,
∵∠AFE=∠BFD,
∴∠FAD=∠CBE,
∴△AFE∽△BCE.
5.证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
6.解:(1)如图,由勾股定理,得
AC==2.
AB==2
故答案是:2,2;
(2)如图所示,BC==2.
又由(1)知,AC=2,AB=2,
∴AC2+BC2=AB2=40,
∴∠ACB=90°.
tan∠1==.
综上所述,∠ACB的值是90°和tan∠1的值是;
(3)△CAB和△DEF相似.理由如下:
如图,DE=DF==,EF==.
则===2,
所以△CAB∽△DEF.
7.解:(1)∵D、E分别是边AB、AC的中点,
∴,DE∥BC.
∴∠AED=∠C.
∵∠F=∠C,
∴∠AED=∠F,
∴FD==4;
(2)∵AB=AC,DE∥BC.
∴∠B=∠C=∠AED=∠ADE,
∵∠AED=∠F,
∴∠ADE=∠F,
又∵∠AED=∠AED,
∴△ADE∽△DFE.
8.解:①△ABC和△DEF相似.理由如下:
∵根据图示知:AB=2,AC=,BC=5,ED=4,DF=2,EF=2,
∴===,
∴△ABC∽△DEF;
②△ACB∽△DP3P2.理由如下:
∵由①知,△ABC∽△DEF,
∴∠D=∠A.
连接DP2P3,DP3=,DP2=,P2P3=.
∵==,
∴△ACB∽△DP3P2.
9.证明:∵CE⊥AB,BF⊥AC,
∴∠AEC=∠AFB=90°.
∵∠A是公共角,
∴△ABF∽△ACE.
∴,
∴,
又∠A是公共角,
∴△AEF∽△ACB.
10.(1)证明:∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,
∴△AEF∽△DCF,
∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
11.(1)证明:
∵△ABC是等边三角形,
∴AC=BA,∠ABD=∠C=60°,
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS);
(2)4对,分别是△BDF∽△BEC,△DBF∽△DAB,△AFE∽△ACD,△AFE∽△BAE,
选择证明△AEF∽△BEA,
∵△ABC是等边三角形,
∴AC=BA,∠C=∠BAE=60°,AC=BC,
∵BD=CE,
∴AE=CD,
∴△ACD≌△BAE(SAS),
∴∠DAC=∠ABE,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA.
12.(1)解:△ABC∽△ADE,△ABD∽△ACE;
(2)△ABD∽△ACE.
证明:由(1)知△ABC∽△ADE,
∴=,
∴AB×AE=AC×AD,
∴=,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
相似三角形的判定
解答题专项练习
一.解答题(共12小题)
1.如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
2.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
3.如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
4.如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
5.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
6.如图,在8×8的正方形网格中,△CAB和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.
(1)填空:AC= ,AB= .
(2)求∠ACB的值和tan∠1的值;
(3)判断△CAB和△DEF是否相似?并说明理由.
7.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.
(1)若BC=8,求FD的长;
(2)若AB=AC,求证:△ADE∽△DFE.
8.如图:方格纸中的每个小正方形边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.
①判断△ABC和△DEF是否相似,并说明理由;
②点P1,P2,P3,D,F都是△DEF边上的5个格点,请在这5个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似.(写出一个即可,并在图中连接相应线段,不必说明理由)
9.如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,求证:△AEF∽△ACB.
10.如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
11.如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.
(1)求证:△ABD≌△BCE;
(2)图中共有 对相似三角形(全等除外).
并请你任选其中一对加以证明.你选择的是 .
12.如图,△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线).
(2)请选择其中的一对三角形,说明其相似的理由.
3.4
相似三角形的判定
解答题专项练习
参考答案与解析
一.解答题(共12小题)
1.解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠ABD=∠ABC=36°=∠A,
在△ADE和△BDE中
∵,
∴△ADE≌△BDE(AAS);
证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠DBC=∠ABC=36°=∠A,
∵∠C=∠C,
∴△ABC∽△BCD.
2.(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴,
∵DF=DC,
∴,
∴,
∴△ABE∽△DEF;
(2)解:∵ABCD为正方形,
∴ED∥BG,
∴,
又∵DF=DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.
3.解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,
∴MN=3;
②图2,作∠ANM=∠B,则△ANM∽△ABC,
有,
∵M为AB中点,AB=,
∴AM=,
∵BC=6,AC=,
∴MN=,
∴MN的长为3或.
4.证明:∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∴∠FAE+∠AFE=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠BFD=90°,
∵∠AFE=∠BFD,
∴∠FAD=∠CBE,
∴△AFE∽△BCE.
5.证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
6.解:(1)如图,由勾股定理,得
AC==2.
AB==2
故答案是:2,2;
(2)如图所示,BC==2.
又由(1)知,AC=2,AB=2,
∴AC2+BC2=AB2=40,
∴∠ACB=90°.
tan∠1==.
综上所述,∠ACB的值是90°和tan∠1的值是;
(3)△CAB和△DEF相似.理由如下:
如图,DE=DF==,EF==.
则===2,
所以△CAB∽△DEF.
7.解:(1)∵D、E分别是边AB、AC的中点,
∴,DE∥BC.
∴∠AED=∠C.
∵∠F=∠C,
∴∠AED=∠F,
∴FD==4;
(2)∵AB=AC,DE∥BC.
∴∠B=∠C=∠AED=∠ADE,
∵∠AED=∠F,
∴∠ADE=∠F,
又∵∠AED=∠AED,
∴△ADE∽△DFE.
8.解:①△ABC和△DEF相似.理由如下:
∵根据图示知:AB=2,AC=,BC=5,ED=4,DF=2,EF=2,
∴===,
∴△ABC∽△DEF;
②△ACB∽△DP3P2.理由如下:
∵由①知,△ABC∽△DEF,
∴∠D=∠A.
连接DP2P3,DP3=,DP2=,P2P3=.
∵==,
∴△ACB∽△DP3P2.
9.证明:∵CE⊥AB,BF⊥AC,
∴∠AEC=∠AFB=90°.
∵∠A是公共角,
∴△ABF∽△ACE.
∴,
∴,
又∠A是公共角,
∴△AEF∽△ACB.
10.(1)证明:∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,
∴△AEF∽△DCF,
∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
11.(1)证明:
∵△ABC是等边三角形,
∴AC=BA,∠ABD=∠C=60°,
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS);
(2)4对,分别是△BDF∽△BEC,△DBF∽△DAB,△AFE∽△ACD,△AFE∽△BAE,
选择证明△AEF∽△BEA,
∵△ABC是等边三角形,
∴AC=BA,∠C=∠BAE=60°,AC=BC,
∵BD=CE,
∴AE=CD,
∴△ACD≌△BAE(SAS),
∴∠DAC=∠ABE,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA.
12.(1)解:△ABC∽△ADE,△ABD∽△ACE;
(2)△ABD∽△ACE.
证明:由(1)知△ABC∽△ADE,
∴=,
∴AB×AE=AC×AD,
∴=,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
