3.4 相似三角形的判定与性质 同步测试(含答案)
文档属性
| 名称 | 3.4 相似三角形的判定与性质 同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-01 11:59:38 | ||
图片预览


文档简介
3.4 相似三角形的判定与性质 同步测试
一.选择题(共10小题)
1.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC
C.AB2=AD?AC D.=
2.如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对 C.2对 D.3对
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B. ∠APB=∠ABC
C.= D.=
4.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A. B.
C. D.
5.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于( )
A. B.
C. D.
6.若两个相似三角形的面积之比为1:4,则它们的最大边的比是( )
A.1:2 B. 1:4 C. 1:5 D. 1:16
7.若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为( )
A.16 B.8 C. 4 D. 2
8.(2015?呼伦贝尔)如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是( )
A.﹣1 B.
C.1 D.
9.在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则等于( )
A. B.
C. D.
10.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
A.4 B. 7
C.3 D.12
二.填空题(共8小题)
11.在△ABC中,AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD= cm.
12.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上中线的比为 .
13.如图,在△ABC中,D、E分别是AB、AC边上的点(DE不平行于BC),当 时(写出一个答案即可),△ADE与△ABC相似.
14.如图,在方格纸中,以每个小方格的边长为单位1,
△ABC和△EPD的顶点均在格点上,请你提供一个符合
条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是 .
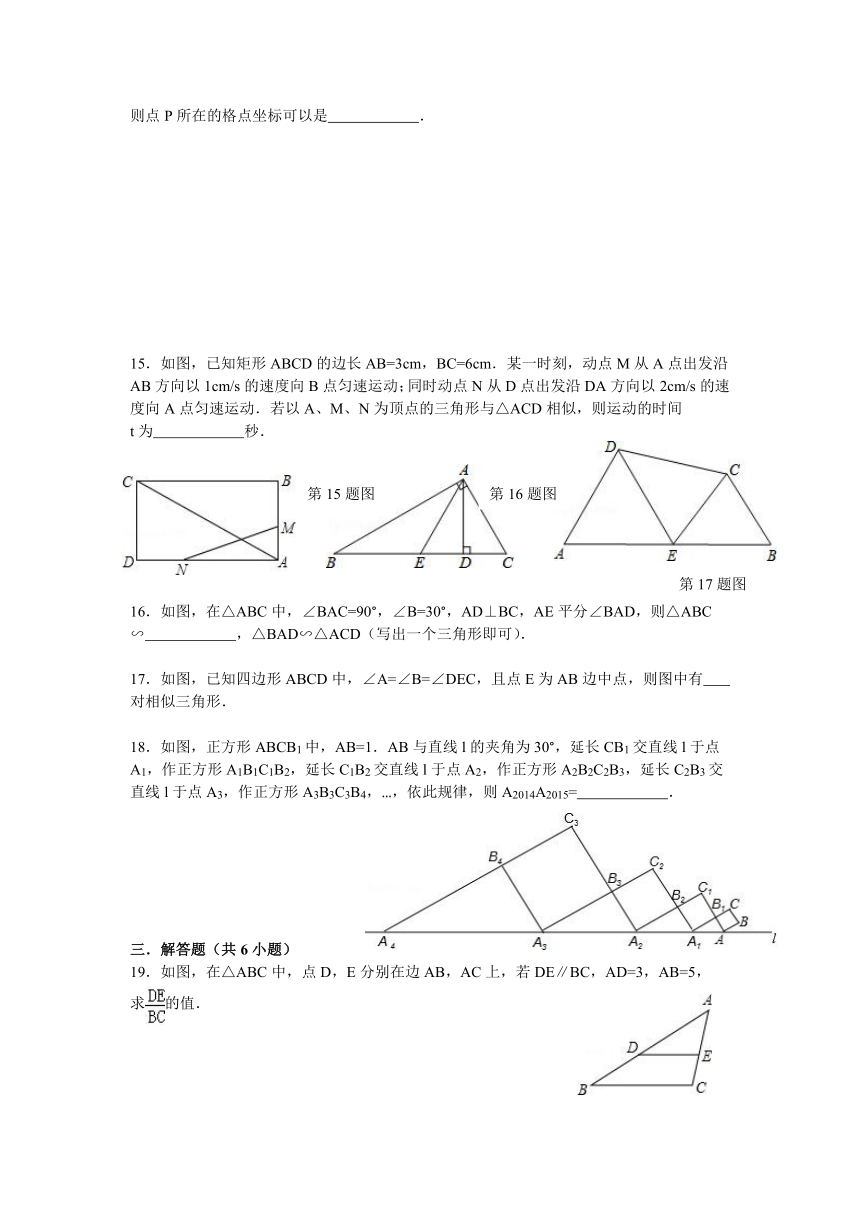
15.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间
t为 秒.
16.如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽ ,△BAD∽△ACD(写出一个三角形即可).
17.如图,已知四边形ABCD中,∠A=∠B=∠DEC,且点E为AB边中点,则图中有 对相似三角形.
18.如图,正方形ABCB1中,AB=1.AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2014A2015= .
三.解答题(共6小题)
19.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,
求的值.
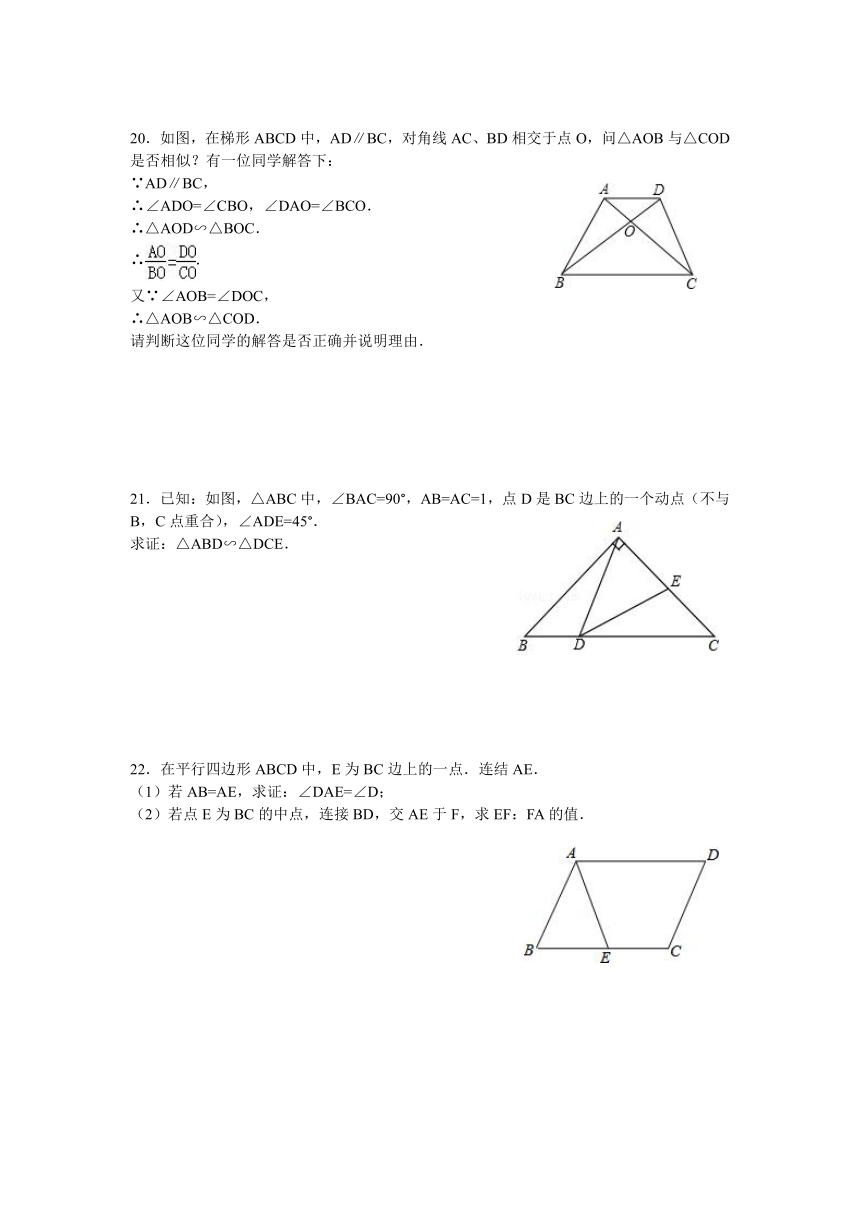
20.如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,问△AOB与△COD是否相似?有一位同学解答下:
∵AD∥BC,
∴∠ADO=∠CBO,∠DAO=∠BCO.
∴△AOD∽△BOC.
∴.
又∵∠AOB=∠DOC,
∴△AOB∽△COD.
请判断这位同学的解答是否正确并说明理由.
21.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
求证:△ABD∽△DCE.
22.在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
23.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
24.在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
3.4 相似三角形的判定与性质 同步测试
参考答案:
一.选择题(共10小题)
1.D 2.D 3.D 4.C 5.A 6.A 7.B 8.A 9.A 10.B
二.填空题(共8小题)
11. 2或 cm. 12. 2:3 .
13. 不唯一,如∠ADE=∠C 14. (3,6) .
15. 2.4或1.5 秒. 16. △DBA (写出一个三角形即可).
17. 3 18. 2()2014 .
三.解答题(共6小题)
19. 解:∵DE∥BC,
∴=,
∵AD=3,AB=5,
∴=.
20.解:不正确,错误的原因是由△AOD∽△BOC得出,
正解是:∵△AOD∽△BOC,
∴,而就不能进一步推出△AOB∽△COD了.
21. 证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
22.证明:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴,
∵E为BC的中点,
∴BE=BC=AD,
∴EF:FA=1:2.
23.解:(1)由题意知,BM=3tcm,CN=2tcm,
∴BN=(8﹣2t)cm,BA==10(cm),
当△BMN∽△BAC时,,
∴,解得:t=;
当△BMN∽△BCA时,,
∴,解得:t=,
∴△BMN与△ABC相似时,t的值为或;
(2)过点M作MD⊥CB于点D,由题意得:
DM=BMsinB=3t=(cm),BD=BMcosB=3t=t(cm),
BM=3tcm,CN=2tcm,
∴CD=(8﹣)cm,
∵AN⊥CM,∠ACB=90°,
∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD,
∵MD⊥CB,
∴∠MDC=∠ACB=90°,
∴△CAN∽△DCM,
∴,
∴=,解得t=.
24.
解:由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3秒时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=cm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3秒;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=秒.
因此t=3秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似.
一.选择题(共10小题)
1.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC
C.AB2=AD?AC D.=
2.如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对 C.2对 D.3对
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B. ∠APB=∠ABC
C.= D.=
4.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A. B.
C. D.
5.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于( )
A. B.
C. D.
6.若两个相似三角形的面积之比为1:4,则它们的最大边的比是( )
A.1:2 B. 1:4 C. 1:5 D. 1:16
7.若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为( )
A.16 B.8 C. 4 D. 2
8.(2015?呼伦贝尔)如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA′是( )
A.﹣1 B.
C.1 D.
9.在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则等于( )
A. B.
C. D.
10.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
A.4 B. 7
C.3 D.12
二.填空题(共8小题)
11.在△ABC中,AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD= cm.
12.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上中线的比为 .
13.如图,在△ABC中,D、E分别是AB、AC边上的点(DE不平行于BC),当 时(写出一个答案即可),△ADE与△ABC相似.
14.如图,在方格纸中,以每个小方格的边长为单位1,
△ABC和△EPD的顶点均在格点上,请你提供一个符合
条件的点P,使△ABC与以E、P、D为顶点的三角形相似,则点P所在的格点坐标可以是 .
15.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间
t为 秒.
16.如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽ ,△BAD∽△ACD(写出一个三角形即可).
17.如图,已知四边形ABCD中,∠A=∠B=∠DEC,且点E为AB边中点,则图中有 对相似三角形.
18.如图,正方形ABCB1中,AB=1.AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2014A2015= .
三.解答题(共6小题)
19.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,
求的值.
20.如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,问△AOB与△COD是否相似?有一位同学解答下:
∵AD∥BC,
∴∠ADO=∠CBO,∠DAO=∠BCO.
∴△AOD∽△BOC.
∴.
又∵∠AOB=∠DOC,
∴△AOB∽△COD.
请判断这位同学的解答是否正确并说明理由.
21.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
求证:△ABD∽△DCE.
22.在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
23.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
24.在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
3.4 相似三角形的判定与性质 同步测试
参考答案:
一.选择题(共10小题)
1.D 2.D 3.D 4.C 5.A 6.A 7.B 8.A 9.A 10.B
二.填空题(共8小题)
11. 2或 cm. 12. 2:3 .
13. 不唯一,如∠ADE=∠C 14. (3,6) .
15. 2.4或1.5 秒. 16. △DBA (写出一个三角形即可).
17. 3 18. 2()2014 .
三.解答题(共6小题)
19. 解:∵DE∥BC,
∴=,
∵AD=3,AB=5,
∴=.
20.解:不正确,错误的原因是由△AOD∽△BOC得出,
正解是:∵△AOD∽△BOC,
∴,而就不能进一步推出△AOB∽△COD了.
21. 证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
22.证明:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BEF∽△AFD,
∴,
∵E为BC的中点,
∴BE=BC=AD,
∴EF:FA=1:2.
23.解:(1)由题意知,BM=3tcm,CN=2tcm,
∴BN=(8﹣2t)cm,BA==10(cm),
当△BMN∽△BAC时,,
∴,解得:t=;
当△BMN∽△BCA时,,
∴,解得:t=,
∴△BMN与△ABC相似时,t的值为或;
(2)过点M作MD⊥CB于点D,由题意得:
DM=BMsinB=3t=(cm),BD=BMcosB=3t=t(cm),
BM=3tcm,CN=2tcm,
∴CD=(8﹣)cm,
∵AN⊥CM,∠ACB=90°,
∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD,
∵MD⊥CB,
∴∠MDC=∠ACB=90°,
∴△CAN∽△DCM,
∴,
∴=,解得t=.
24.
解:由题意得AP=4t,CQ=2t,则CP=20﹣4t,
(1)当t=3秒时,CP=20﹣4t=8cm,CQ=2t=6cm,
由勾股定理得PQ=;
(2)由题意得AP=4t,CQ=2t,则CP=20﹣4t,
因此Rt△CPQ的面积为S=cm2;
(3)分两种情况:
①当Rt△CPQ∽Rt△CAB时,,即,解得t=3秒;
②当Rt△CPQ∽Rt△CBA时,,即,解得t=秒.
因此t=3秒或t=秒时,以点C、P、Q为顶点的三角形与△ABC相似.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
