3.4 相似三角形与三角函数 同步练习(无答案)
文档属性
| 名称 | 3.4 相似三角形与三角函数 同步练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-01 12:00:58 | ||
图片预览



文档简介
3.4 相似三角形与三角函数
班别: 姓名: 学号:
一、填空题
1、已知三角形相邻两边长为20cm、30cm,第三边上的高10cm,则此三角形面积为 。
2、已知一商场自动扶梯L为10米,该自动扶梯到达高度h=6米,自动扶梯与地面所成角为,则tan的值是 。
3、AB的垂直平分线DE交BC延长线于E,则CE= 。
4、如图是某商场一楼与二楼间的手扶电梯示意图,其中AB、CD分别表示一楼二楼地面的水平线,则乘电梯从B到C上升的高度h是 。
5、是放置在正方形网格中的一个角,则 。
6、在P是AB上一点,AP=2BP,于Q,连AQ,则。
7、中,,把AB翻折,使AB落在BC边上,A落在E处,折痕为BD,则。
8、中,D、E分别是AB、AC中点,连DE,BE和CD相交于O点,OD=2,则OC= 。
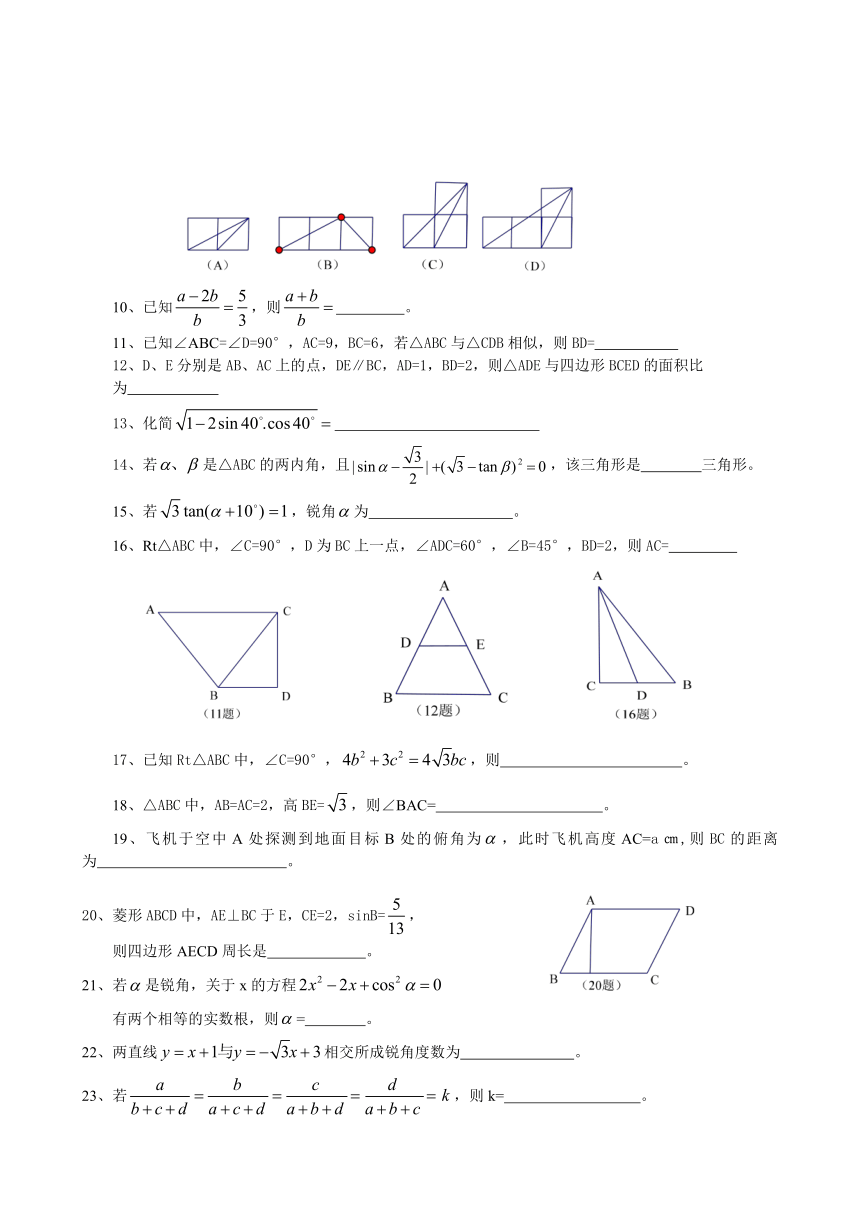
9、正方形边长都为1,则下列图中的三
角形与相似的是( )
10、已知,则 。
11、已知∠ABC=∠D=90°,AC=9,BC=6,若△ABC与△CDB相似,则BD=
12、D、E分别是AB、AC上的点,DE∥BC,AD=1,BD=2,则△ADE与四边形BCED的面积比
为
13、化简
14、若是△ABC的两内角,且,该三角形是 三角形。
15、若,锐角为 。
16、Rt△ABC中,∠C=90°,D为BC上一点,∠ADC=60°,∠B=45°,BD=2,则AC=
17、已知Rt△ABC中,∠C=90°,,则 。
18、△ABC中,AB=AC=2,高BE=,则∠BAC= 。
19、飞机于空中A处探测到地面目标B处的俯角为,此时飞机高度AC=a㎝,则BC的距离为 。
20、菱形ABCD中,AE⊥BC于E,CE=2,sinB=,
则四边形AECD周长是 。
21、若是锐角,关于x的方程
有两个相等的实数根,则= 。
22、两直线相交所成锐角度数为 。
23、若,则k= 。
24、△ABC与△DEF是位似图形,位似比是,AB=4,则DE= 。
25、中,A、B两个顶点在X轴上方,C(-1,0),以O为位似中心,在X轴下方作的位似图形,并把边长放大到原来的2倍,记所得的像是,该点B的对应点的横坐标是a,则B的横坐标是 。
26、平行四边形ABCD中,E在CD上,若DE:EC=1:2,则DF:BE= 。
27、如图,M是内一点,过M分别作EF∥BC,PQ∥AB,GH∥AC,已知△EMG、△MPE、△MQH的面积分别为4,9,49,则。
28、Rt△ABC中,,AC=12,BC=5,则CD= ,BD= 。
29、△ABC中,AB=9,AC=6,M在AB上,且AM=3,N在AC上,连MN,使△AMN与原三角形相似,AN= 。
30、若D、E分别为△ABC的边BC、AC中点,BE与AD相交于G,EF∥BC交AD于F,则AF:FG= 。
31、平行四边形ABCD中,E是AD延长线上一点,D是AE的黄金分割点,AD>DE,BE、CD相交于F,AB=,则CF= 。
32、计算=
32、是锐角,且,则= 。
33、①时,。
②时且,则 。
③若是锐角,,则=
34、计算 (其中)
35、计算
36、Rt△ABC中,,高AD=4,,则AC= 。
37、已知Rt△ABC中,,则C= 。
38、△ABC中,,P是△ABC内一点,,且PA=8,PC=6,则PB= 。
39、正方形DEFG在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知△ABC的边BC长60cm,高AH为40cm,则正方形DEFG的边长是 。
40、已知DE是△ABC中位线,M是DE中点,CM延长线交AB于N,则
。
41、在四边形ABCD,E是AB上一点,EC∥AD,DE∥BC,,,则。
42、△ABC中,a,b,c分别是的对边,已知,,,则。
43、设,,则。
44、△ABC周长是24,M是AB中点,MC=AM=5,则△ABC的面积为 。
45、△ABC中,a,b,c分别是的对边,a=15,b=17,(为定值)若满足上述条件的三角形的唯一存在的,则∠A= 。
二、选择题
46、已知a,b,c为正数,且,下列四点中,在正比例函数y=mx的图象上的点坐标是( )
A、 B、(1,2) C、 D、(1,-1)
47、D、E、F、G分别在△ABC的AC、AB边上,
且DF∥EG∥BC,AF=FG=GB,则△ADF、△AEG、
△ACB相似比是( )
48、下列命题正确的是( )
A、全等图形一定是位似图形
B、相似图形一定是位似图形
C、位似图形一定是全等图形
D、位似图形一定是相似图形
49、设,则一定经过 象限。
A、一、二 B、一、三 C、二、四 D、一、三、四
50、矩形长边和短边分别为,1,则矩形两对角线所成锐角的正弦值为( )
A、 B、 C、 D、
51、已知为锐角,,则的度数为( )
A、30 B、45 C、60 D、75
52、一架5m长的梯子斜靠在墙上,它与地面夹角是40°,则梯子底端到墙的距离为( )A、 B、 C、 D、
53、中,,AC=8,的平分线,则BC= 。
A、 B、 C、 D、16
54、若是锐角,,则的取值范围是( )
A、 B、 C、 D、
55、一个家庭有3个孩子,这个家庭有3个男孩的概率是( )
A、 B、 C、 D、
56、下列一定能够相似的一组三角形为( )
A、两个等腰三角形 B、两个直角三角形
C、两个等边三角形 D、两个锐角三角形
57、在△ABC中,D在BC上,△ABC∽△DBA,
下列结论对的是( )
A、AB2=BC·BD B、AB2=AC·BD
C、AB·AD=BD·BC D、AB·AD=AD·CD
58、下列条件中,能使△ABC与△A'B'C'相似的是( )
①、AB=1.5,BC=2,AC=2.5, B'C'=16,A'B'=12,A'C=20,∠A=88°,∠A'=88°
②、BC=8,AC=7,B'C'=16,A'C'=14,
③、,AC=15,AB=7,,A'B'=14,A'C'=30
④、AC=6,BC=8,AB=4,A'B'=12,B'C'=24,A'C'=18
⑤、,,,
A、1组 B、2组 C、3组 D、4组
59、CD是斜边AB上的高,下列各式不正确的是( )
A、=BD·AB B、=AD·AB C、·=BD·AD D、BC·AD=AC·BD
60、给出下列条件,①,
②,③,
④=AD·AB,其中单独能判
定△ABC∽△ACD的个数是( )
A、1 B、2 C、3 D、4
61、的大小关系是( )
A、 B、
C、 D、
62、△ABC中,,下列结论错误的是( )
A、 B、sinB=tanB·cosB C、 D、sinA=cosB
63、,下列条件中不能解直角三角形的是( )
A、已知a,b或b,c B、已知 C、已知a,b D、已知a,
64、,c=3b,则cosA=( )
A、 B、 C、 D、
65、身高相同的甲、乙、丙三人放风筝,各人放出的线长分别为300m、250m、200m,线与地面所成角度分别为30o,45o,60o(风筝线是拉直的),则三人所放风筝最高的是( )
A、甲 B、乙 C、丙 D、一样高
66、已知,是锐角,则( )
A、 B、 C、 D、
67、△ABC中,AB=AC=6,BC=8,AE平分交BC于E点,D为AB中点,连DE,则△BDE的周长是( )
A、 B、10 C、 D、12
68、如图所示是重叠的两个直角三角形,将其中一
个直角三角形沿BC方向平移得到△DEF,若AB=8cm,
BE=4cm,DH=3cm,则图中阴影部分的面积为( )
A、24 B、25 C、26 D、27
三、解答题
69、在梯形ABCD中,AD∥BC,AB=CD,过D作DEBC,延长DE至F使EF=DE,连BF、CF、AC。
(1)求证:四边表ABFC是平行四边形。
(2)如果=BE·CE,求证四边形ABFC是矩形。
70、在等腰△ABC中,AB=AC,D为CB延长线一点,E为BC延长线一点,满足=DB·CE。
(1)试说明△ADB∽△EAC。
(2)若,求度数。
71、在平行四边形ABCD中,过A作AEBC,垂足为E,。
(1)求证:△ADF∽△DEC。
(2)若AB=4,AD=,AE=3,求AF。
72、△ABC是直角三角形,于D,E是AC中点,ED的延长线与CB延长线交于点F。
(1)求证:FB·FC。
(2)若G是BC中点,连GD,GD与EF垂直吗?为什么?
73、在,P是BC上一动点,PD∥AB,PD与AC相交于D,连AP。
(1)求AC、BC。
(2)设PC=X,△ADP面积为y,问当X为何值时,y最大?并求出最大值。
74、如图,登山队员在山脚A点测得山顶B的仰角,测得倾斜角30o的斜坡前进100米到达D点后,又在D点测得山顶B的仰角为60o,求山高BC。
(精确到1米,参考数据:)
75、如图所示E、F分别是AB、AC上一点,连CE、BF相交于O,连AO分别交EF于M,交BC于G。已知EF∥BC。
求证:(1)ME=MF。
(2)BG=CG。
76、如图有一批形状大小相同的不锈钢片,呈直角三角形。已知,AB=5cm,BC=3cm,试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片,求这种正方形钢片的边长。
班别: 姓名: 学号:
一、填空题
1、已知三角形相邻两边长为20cm、30cm,第三边上的高10cm,则此三角形面积为 。
2、已知一商场自动扶梯L为10米,该自动扶梯到达高度h=6米,自动扶梯与地面所成角为,则tan的值是 。
3、AB的垂直平分线DE交BC延长线于E,则CE= 。
4、如图是某商场一楼与二楼间的手扶电梯示意图,其中AB、CD分别表示一楼二楼地面的水平线,则乘电梯从B到C上升的高度h是 。
5、是放置在正方形网格中的一个角,则 。
6、在P是AB上一点,AP=2BP,于Q,连AQ,则。
7、中,,把AB翻折,使AB落在BC边上,A落在E处,折痕为BD,则。
8、中,D、E分别是AB、AC中点,连DE,BE和CD相交于O点,OD=2,则OC= 。
9、正方形边长都为1,则下列图中的三
角形与相似的是( )
10、已知,则 。
11、已知∠ABC=∠D=90°,AC=9,BC=6,若△ABC与△CDB相似,则BD=
12、D、E分别是AB、AC上的点,DE∥BC,AD=1,BD=2,则△ADE与四边形BCED的面积比
为
13、化简
14、若是△ABC的两内角,且,该三角形是 三角形。
15、若,锐角为 。
16、Rt△ABC中,∠C=90°,D为BC上一点,∠ADC=60°,∠B=45°,BD=2,则AC=
17、已知Rt△ABC中,∠C=90°,,则 。
18、△ABC中,AB=AC=2,高BE=,则∠BAC= 。
19、飞机于空中A处探测到地面目标B处的俯角为,此时飞机高度AC=a㎝,则BC的距离为 。
20、菱形ABCD中,AE⊥BC于E,CE=2,sinB=,
则四边形AECD周长是 。
21、若是锐角,关于x的方程
有两个相等的实数根,则= 。
22、两直线相交所成锐角度数为 。
23、若,则k= 。
24、△ABC与△DEF是位似图形,位似比是,AB=4,则DE= 。
25、中,A、B两个顶点在X轴上方,C(-1,0),以O为位似中心,在X轴下方作的位似图形,并把边长放大到原来的2倍,记所得的像是,该点B的对应点的横坐标是a,则B的横坐标是 。
26、平行四边形ABCD中,E在CD上,若DE:EC=1:2,则DF:BE= 。
27、如图,M是内一点,过M分别作EF∥BC,PQ∥AB,GH∥AC,已知△EMG、△MPE、△MQH的面积分别为4,9,49,则。
28、Rt△ABC中,,AC=12,BC=5,则CD= ,BD= 。
29、△ABC中,AB=9,AC=6,M在AB上,且AM=3,N在AC上,连MN,使△AMN与原三角形相似,AN= 。
30、若D、E分别为△ABC的边BC、AC中点,BE与AD相交于G,EF∥BC交AD于F,则AF:FG= 。
31、平行四边形ABCD中,E是AD延长线上一点,D是AE的黄金分割点,AD>DE,BE、CD相交于F,AB=,则CF= 。
32、计算=
32、是锐角,且,则= 。
33、①时,。
②时且,则 。
③若是锐角,,则=
34、计算 (其中)
35、计算
36、Rt△ABC中,,高AD=4,,则AC= 。
37、已知Rt△ABC中,,则C= 。
38、△ABC中,,P是△ABC内一点,,且PA=8,PC=6,则PB= 。
39、正方形DEFG在△ABC的边BC上,顶点D、G分别在边AB、AC上,已知△ABC的边BC长60cm,高AH为40cm,则正方形DEFG的边长是 。
40、已知DE是△ABC中位线,M是DE中点,CM延长线交AB于N,则
。
41、在四边形ABCD,E是AB上一点,EC∥AD,DE∥BC,,,则。
42、△ABC中,a,b,c分别是的对边,已知,,,则。
43、设,,则。
44、△ABC周长是24,M是AB中点,MC=AM=5,则△ABC的面积为 。
45、△ABC中,a,b,c分别是的对边,a=15,b=17,(为定值)若满足上述条件的三角形的唯一存在的,则∠A= 。
二、选择题
46、已知a,b,c为正数,且,下列四点中,在正比例函数y=mx的图象上的点坐标是( )
A、 B、(1,2) C、 D、(1,-1)
47、D、E、F、G分别在△ABC的AC、AB边上,
且DF∥EG∥BC,AF=FG=GB,则△ADF、△AEG、
△ACB相似比是( )
48、下列命题正确的是( )
A、全等图形一定是位似图形
B、相似图形一定是位似图形
C、位似图形一定是全等图形
D、位似图形一定是相似图形
49、设,则一定经过 象限。
A、一、二 B、一、三 C、二、四 D、一、三、四
50、矩形长边和短边分别为,1,则矩形两对角线所成锐角的正弦值为( )
A、 B、 C、 D、
51、已知为锐角,,则的度数为( )
A、30 B、45 C、60 D、75
52、一架5m长的梯子斜靠在墙上,它与地面夹角是40°,则梯子底端到墙的距离为( )A、 B、 C、 D、
53、中,,AC=8,的平分线,则BC= 。
A、 B、 C、 D、16
54、若是锐角,,则的取值范围是( )
A、 B、 C、 D、
55、一个家庭有3个孩子,这个家庭有3个男孩的概率是( )
A、 B、 C、 D、
56、下列一定能够相似的一组三角形为( )
A、两个等腰三角形 B、两个直角三角形
C、两个等边三角形 D、两个锐角三角形
57、在△ABC中,D在BC上,△ABC∽△DBA,
下列结论对的是( )
A、AB2=BC·BD B、AB2=AC·BD
C、AB·AD=BD·BC D、AB·AD=AD·CD
58、下列条件中,能使△ABC与△A'B'C'相似的是( )
①、AB=1.5,BC=2,AC=2.5, B'C'=16,A'B'=12,A'C=20,∠A=88°,∠A'=88°
②、BC=8,AC=7,B'C'=16,A'C'=14,
③、,AC=15,AB=7,,A'B'=14,A'C'=30
④、AC=6,BC=8,AB=4,A'B'=12,B'C'=24,A'C'=18
⑤、,,,
A、1组 B、2组 C、3组 D、4组
59、CD是斜边AB上的高,下列各式不正确的是( )
A、=BD·AB B、=AD·AB C、·=BD·AD D、BC·AD=AC·BD
60、给出下列条件,①,
②,③,
④=AD·AB,其中单独能判
定△ABC∽△ACD的个数是( )
A、1 B、2 C、3 D、4
61、的大小关系是( )
A、 B、
C、 D、
62、△ABC中,,下列结论错误的是( )
A、 B、sinB=tanB·cosB C、 D、sinA=cosB
63、,下列条件中不能解直角三角形的是( )
A、已知a,b或b,c B、已知 C、已知a,b D、已知a,
64、,c=3b,则cosA=( )
A、 B、 C、 D、
65、身高相同的甲、乙、丙三人放风筝,各人放出的线长分别为300m、250m、200m,线与地面所成角度分别为30o,45o,60o(风筝线是拉直的),则三人所放风筝最高的是( )
A、甲 B、乙 C、丙 D、一样高
66、已知,是锐角,则( )
A、 B、 C、 D、
67、△ABC中,AB=AC=6,BC=8,AE平分交BC于E点,D为AB中点,连DE,则△BDE的周长是( )
A、 B、10 C、 D、12
68、如图所示是重叠的两个直角三角形,将其中一
个直角三角形沿BC方向平移得到△DEF,若AB=8cm,
BE=4cm,DH=3cm,则图中阴影部分的面积为( )
A、24 B、25 C、26 D、27
三、解答题
69、在梯形ABCD中,AD∥BC,AB=CD,过D作DEBC,延长DE至F使EF=DE,连BF、CF、AC。
(1)求证:四边表ABFC是平行四边形。
(2)如果=BE·CE,求证四边形ABFC是矩形。
70、在等腰△ABC中,AB=AC,D为CB延长线一点,E为BC延长线一点,满足=DB·CE。
(1)试说明△ADB∽△EAC。
(2)若,求度数。
71、在平行四边形ABCD中,过A作AEBC,垂足为E,。
(1)求证:△ADF∽△DEC。
(2)若AB=4,AD=,AE=3,求AF。
72、△ABC是直角三角形,于D,E是AC中点,ED的延长线与CB延长线交于点F。
(1)求证:FB·FC。
(2)若G是BC中点,连GD,GD与EF垂直吗?为什么?
73、在,P是BC上一动点,PD∥AB,PD与AC相交于D,连AP。
(1)求AC、BC。
(2)设PC=X,△ADP面积为y,问当X为何值时,y最大?并求出最大值。
74、如图,登山队员在山脚A点测得山顶B的仰角,测得倾斜角30o的斜坡前进100米到达D点后,又在D点测得山顶B的仰角为60o,求山高BC。
(精确到1米,参考数据:)
75、如图所示E、F分别是AB、AC上一点,连CE、BF相交于O,连AO分别交EF于M,交BC于G。已知EF∥BC。
求证:(1)ME=MF。
(2)BG=CG。
76、如图有一批形状大小相同的不锈钢片,呈直角三角形。已知,AB=5cm,BC=3cm,试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片,求这种正方形钢片的边长。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
