人教版七年级上册第4章《4.1.1 立体图形与平面图形》同步练习(含答案)
文档属性
| 名称 | 人教版七年级上册第4章《4.1.1 立体图形与平面图形》同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-01 00:00:00 | ||
图片预览



文档简介
第四章
几何图形初步
4.1
几何图形
4.1.1
立体图形与平面图形
第1课时
认识立体图形和几何图形
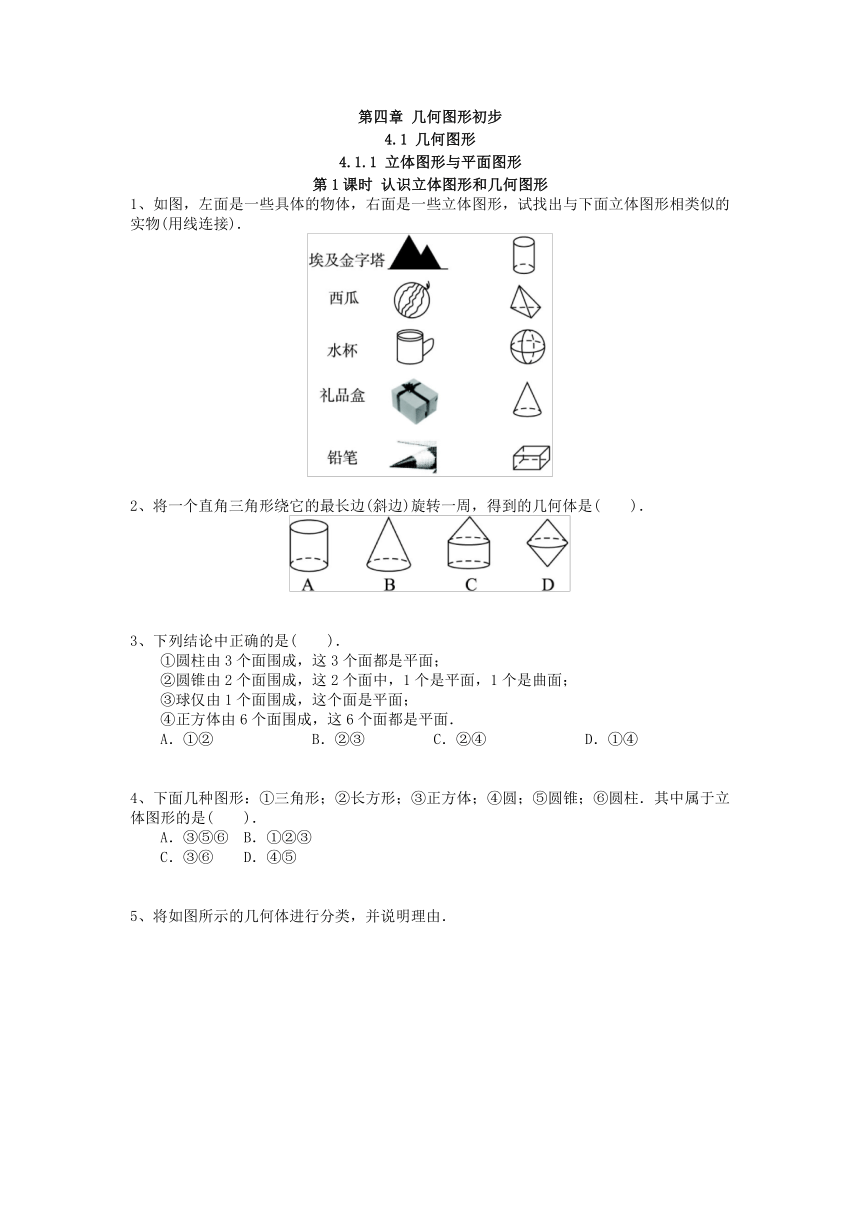
1、如图,左面是一些具体的物体,右面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
2、将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( ).
3、下列结论中正确的是( ).
①圆柱由3个面围成,这3个面都是平面;
②圆锥由2个面围成,这2个面中,1个是平面,1个是曲面;
③球仅由1个面围成,这个面是平面;
④正方体由6个面围成,这6个面都是平面.
①②
B.②③
C.②④
D.①④
4、下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( ).
A.③⑤⑥
B.①②③
C.③⑥
D.④⑤
5、将如图所示的几何体进行分类,并说明理由.
6、如图所示的八棱柱,它的底面边长都是5厘米,侧棱长都是6厘米,回答下列问题:
(1)这个八棱柱一共有多少面?它们的形状分别是什么图形?哪些面的形状、面积完全相同?
(2)这个八棱柱一共有多少条棱?多少个顶点?
(3)沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是什么形状?面积是多少?
参考答案
1、答案:如图所示:
2、解析:
A
×
圆柱是由一长方形绕其一边长旋转而成的
B
×
圆锥是由一直角三角形绕其直角边旋转而成的
C
×
该几何体是由直角梯形绕其下底旋转而成的
D
√
该几何体是由直角三角形绕其斜边旋转而成的
答案:D
3、解析:
①
×
圆柱由3个面围成,其中两底面是平面,侧面是曲面,所以①错误.
②
√
圆锥由2个面围成,其中底面是平面,侧面是曲面,所以②正确.
③
×
球是由1个面围成的,这个面是曲面,所以③错误.
④
√
正方体是一个多面体,它是由6个平面围成的,所以④正确.
答案:C
4、解析:三角形、长方形、正方形、圆是平面图形;正方体、圆锥、圆柱是立体图形.
答案:A
5、分析:几何体的分类不是唯一的.我们应先观察各个几何体,努力发现其共同点,然后可根据其共同点来进行适当的分类.
解:若按柱体、锥体、球体来分类:(2)(3)(5)(6)是柱体,(4)是锥体,(1)是球体;
若按几何体的面是否含有曲面来分类,则(1)(4)(6)是旋转体,(2)(3)(5)是多面体.
6、解:(1)这个八棱柱一共有10个面,上下两个底面是八边形,八个侧面都是长方形;上下两个底面的形状、面积完全相同,八个侧面形状、面积完全相同.
(2)这个八棱柱一共有24条棱,16个顶点.
(3)沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是长方形,长为5×8=40(厘米),宽为6厘米,所以面积是40×6=240(平方厘米).
第四章
几何图形初步
4.1几何图形
4.1.1
几何图形与平面图形
第2课时
从不同的方向看立体图形和立体图形的展开图
一、选择题
1.由四个大小相同的正方体组成的几何体如图所示,那么它的俯视图是(
).
2.如图所示的四种物体中,哪种物体最接近于圆柱(
).
3.如图是一正方体纸盒的展开图,每个面上都标注了字母或数字,则面a在展开前所对的面上的数字是(
).
A.2
B.3
C.4
D.5
4.按如图所示的图形中的虚线折叠可以围成一个棱柱的是(
).
5.如图所示,下列图形绕着虚线旋转一周得到圆锥体的是
(
)
6.将左图中的正方体纸盒沿所示的粗线剪开,其平面展开图的示意图为( )
A.
B.
C.
D.
二、填空题
7.五棱柱有________个顶点,________条棱,________个面.
8.柱体包括________和________,锥体包括________和________.
9.一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“超”相对的字是________.
10.(内蒙古赤峰)如图所示是一个几何体的三视图,则这个几何体是________.
11.圆锥的底面是__________形,侧面是__________的面,侧面展开图是__________形.
12.当笔尖在纸上移动时,形成_______,这说明:_____;表针旋转时,形成了一个
,这说明:
;长方形纸片绕它的一边旋转,形成的几何图形就是
,这说明:
.
三、解答题
13.
如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的上面,那么哪一面会在下面
(2)如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面
(3)从右面看是面A,从上面看是面E,那么哪一面会在前面
14.如图所示是一个机器零件从正面看和从上面看所得到的图形,求该零件的体积(取3.14,单位:mm)(提示:底面积×高).
15.
如图所示的一张硬纸片,它能否折成一个长方体盒子?若能,说明理由,并画出它的立体图形,计算它的体积.
参考答案
一、选择题
1.B;
2.A;
3.B;【解析】要求面a在展开前所对的面上的数字,我们可以把正方体的展开图折叠起来,则面a、2、3、4按照第一、三个对应,第二、四个对应,于是面a在展开前所对的面上的数字为3.
4.
C
;【解析】A、D中两个底面不能放在同一侧,B中侧面个数与底面边数不等,故选C.
5.
D
;【解析】选项A、B、C、D中的图形旋转一周分别形成圆台、球、圆柱和圆锥,故选D.
6.
C;【解析】由正方体的表面展开图的特点再结合实际操作,便可得解.
二、填空题
7.
10,
15,
7
;【解析】五棱柱上底面有5个顶点,下底面有5个顶点,共10个顶点;上、下底面各有5条棱,竖直有5条棱,共15条棱;7个面,其中5个侧面,2个底面.
8.
圆柱,棱柱;
圆锥,棱锥
9.
自;【解析】要弄清立体图形与其平面展开图各部分间的关系,需要较强的空间想象能力,这种能力是建立在动手操作、认真观察与善于思考的基础上.
10.三棱柱(或填正三棱柱)
;【解析】考查空间想象能力.
11.圆,曲,扇
;【解析】动手操作或空间想象,便得答案.
12.一条线,点动成线;圆面,线动成面;圆柱体,面动成体
三、解答题
13.解:(1)如果面A在多面体的上面,那么面C会在下面.
(2)如果面,在多面体的后面,从左面看是面C,那么向外折时面C会在上面,向里折时面A会在上面.
(3)从右面看是面A,从上面看是面E,那么向外折时从前面看是面B,向里折时从前面看是面D.
14.解:(mm3),
即该零件的体积为40048
mm3.
提示:由该零件从正面看和从上面看所得到的图形可以确定该零件是由上、下两部分组成的,上面是一个高为32
mm,底面直径为20
mm的圆柱;下面是一个长为30
mm,宽为25
mm,高为40
mm的长方体,零件的体积是圆柱与长方体体积之和.
15.
【解析】
解:能折成一个长方体盒子,因为符合长方体的平面展开图的所有条件,该几何体的立体图形如图所示.此长方体的长为5m,宽为2m,高为3m,所以它的体积为:
5×2×3=30(m3).
几何图形初步
4.1
几何图形
4.1.1
立体图形与平面图形
第1课时
认识立体图形和几何图形
1、如图,左面是一些具体的物体,右面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
2、将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( ).
3、下列结论中正确的是( ).
①圆柱由3个面围成,这3个面都是平面;
②圆锥由2个面围成,这2个面中,1个是平面,1个是曲面;
③球仅由1个面围成,这个面是平面;
④正方体由6个面围成,这6个面都是平面.
①②
B.②③
C.②④
D.①④
4、下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( ).
A.③⑤⑥
B.①②③
C.③⑥
D.④⑤
5、将如图所示的几何体进行分类,并说明理由.
6、如图所示的八棱柱,它的底面边长都是5厘米,侧棱长都是6厘米,回答下列问题:
(1)这个八棱柱一共有多少面?它们的形状分别是什么图形?哪些面的形状、面积完全相同?
(2)这个八棱柱一共有多少条棱?多少个顶点?
(3)沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是什么形状?面积是多少?
参考答案
1、答案:如图所示:
2、解析:
A
×
圆柱是由一长方形绕其一边长旋转而成的
B
×
圆锥是由一直角三角形绕其直角边旋转而成的
C
×
该几何体是由直角梯形绕其下底旋转而成的
D
√
该几何体是由直角三角形绕其斜边旋转而成的
答案:D
3、解析:
①
×
圆柱由3个面围成,其中两底面是平面,侧面是曲面,所以①错误.
②
√
圆锥由2个面围成,其中底面是平面,侧面是曲面,所以②正确.
③
×
球是由1个面围成的,这个面是曲面,所以③错误.
④
√
正方体是一个多面体,它是由6个平面围成的,所以④正确.
答案:C
4、解析:三角形、长方形、正方形、圆是平面图形;正方体、圆锥、圆柱是立体图形.
答案:A
5、分析:几何体的分类不是唯一的.我们应先观察各个几何体,努力发现其共同点,然后可根据其共同点来进行适当的分类.
解:若按柱体、锥体、球体来分类:(2)(3)(5)(6)是柱体,(4)是锥体,(1)是球体;
若按几何体的面是否含有曲面来分类,则(1)(4)(6)是旋转体,(2)(3)(5)是多面体.
6、解:(1)这个八棱柱一共有10个面,上下两个底面是八边形,八个侧面都是长方形;上下两个底面的形状、面积完全相同,八个侧面形状、面积完全相同.
(2)这个八棱柱一共有24条棱,16个顶点.
(3)沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是长方形,长为5×8=40(厘米),宽为6厘米,所以面积是40×6=240(平方厘米).
第四章
几何图形初步
4.1几何图形
4.1.1
几何图形与平面图形
第2课时
从不同的方向看立体图形和立体图形的展开图
一、选择题
1.由四个大小相同的正方体组成的几何体如图所示,那么它的俯视图是(
).
2.如图所示的四种物体中,哪种物体最接近于圆柱(
).
3.如图是一正方体纸盒的展开图,每个面上都标注了字母或数字,则面a在展开前所对的面上的数字是(
).
A.2
B.3
C.4
D.5
4.按如图所示的图形中的虚线折叠可以围成一个棱柱的是(
).
5.如图所示,下列图形绕着虚线旋转一周得到圆锥体的是
(
)
6.将左图中的正方体纸盒沿所示的粗线剪开,其平面展开图的示意图为( )
A.
B.
C.
D.
二、填空题
7.五棱柱有________个顶点,________条棱,________个面.
8.柱体包括________和________,锥体包括________和________.
9.一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“超”相对的字是________.
10.(内蒙古赤峰)如图所示是一个几何体的三视图,则这个几何体是________.
11.圆锥的底面是__________形,侧面是__________的面,侧面展开图是__________形.
12.当笔尖在纸上移动时,形成_______,这说明:_____;表针旋转时,形成了一个
,这说明:
;长方形纸片绕它的一边旋转,形成的几何图形就是
,这说明:
.
三、解答题
13.
如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的上面,那么哪一面会在下面
(2)如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面
(3)从右面看是面A,从上面看是面E,那么哪一面会在前面
14.如图所示是一个机器零件从正面看和从上面看所得到的图形,求该零件的体积(取3.14,单位:mm)(提示:底面积×高).
15.
如图所示的一张硬纸片,它能否折成一个长方体盒子?若能,说明理由,并画出它的立体图形,计算它的体积.
参考答案
一、选择题
1.B;
2.A;
3.B;【解析】要求面a在展开前所对的面上的数字,我们可以把正方体的展开图折叠起来,则面a、2、3、4按照第一、三个对应,第二、四个对应,于是面a在展开前所对的面上的数字为3.
4.
C
;【解析】A、D中两个底面不能放在同一侧,B中侧面个数与底面边数不等,故选C.
5.
D
;【解析】选项A、B、C、D中的图形旋转一周分别形成圆台、球、圆柱和圆锥,故选D.
6.
C;【解析】由正方体的表面展开图的特点再结合实际操作,便可得解.
二、填空题
7.
10,
15,
7
;【解析】五棱柱上底面有5个顶点,下底面有5个顶点,共10个顶点;上、下底面各有5条棱,竖直有5条棱,共15条棱;7个面,其中5个侧面,2个底面.
8.
圆柱,棱柱;
圆锥,棱锥
9.
自;【解析】要弄清立体图形与其平面展开图各部分间的关系,需要较强的空间想象能力,这种能力是建立在动手操作、认真观察与善于思考的基础上.
10.三棱柱(或填正三棱柱)
;【解析】考查空间想象能力.
11.圆,曲,扇
;【解析】动手操作或空间想象,便得答案.
12.一条线,点动成线;圆面,线动成面;圆柱体,面动成体
三、解答题
13.解:(1)如果面A在多面体的上面,那么面C会在下面.
(2)如果面,在多面体的后面,从左面看是面C,那么向外折时面C会在上面,向里折时面A会在上面.
(3)从右面看是面A,从上面看是面E,那么向外折时从前面看是面B,向里折时从前面看是面D.
14.解:(mm3),
即该零件的体积为40048
mm3.
提示:由该零件从正面看和从上面看所得到的图形可以确定该零件是由上、下两部分组成的,上面是一个高为32
mm,底面直径为20
mm的圆柱;下面是一个长为30
mm,宽为25
mm,高为40
mm的长方体,零件的体积是圆柱与长方体体积之和.
15.
【解析】
解:能折成一个长方体盒子,因为符合长方体的平面展开图的所有条件,该几何体的立体图形如图所示.此长方体的长为5m,宽为2m,高为3m,所以它的体积为:
5×2×3=30(m3).
