函数的性质----单调性教案
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
【课题】 3.3.3函数的基本性质 —— 单调性
【教学目标】
知识目标:⑴ 理解函数的单调性的概念; ⑵ 会借助于函数图像讨论函数的单调性。
能力目标:通过利用函数图像研究函数性质,培养学生的观察能力。
情感目标:通过生活实例中的问题,让学生感悟数学的实用性。
【教学重点】理解函数单调性的概念及其图像特征,写出函数的单调区间。
【教学难点】抽象出函数单调性的定义。
【教学设计】
(1)用学生熟悉的主题活动将所学的知识有机的结合在一起;
(2)引导学生去感知数学的数形结合思想。通过图形认识特征,由此定义概念,再利用图形(或定义)进行判断;
(3)在问题的思考、交流、解决中培养和发展学生的思维能力。
【教学方法】启发式、探究式、发现式。
【授课班级】09模具(2)班(多媒体1室)
【授课教师】刘其明
【授课时间】第4周星期五第2节(2010年3月19日)
【教学过程】
一、创设情景,兴趣导入,完成前置任务。
问题1
(1)由于某种原因,2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日,请查阅资料说明做出这个决定的主要原因。
(2)通过查阅历史资料研究北京奥运会开幕式当天的气温变化情况,并画出图象。
问题2
下图为股市中,某股票在半天内的行情,请描述此股票的涨幅情况。
归纳
类似地,函数值随着自变量的增大而增大(或减小)的性质就是函数的单调性。
二、动脑思考,探索新知,讲授新课。
概念
在定义域的某个区间上,函数值随着自变量的增大而增大(或减小)的性质叫做函数的单调性。
类型
(1)如图(1)所示,在定义域的某个区间上,若自变量增大时,函数值也随着增大,则称函数在这个区间上是增函数。这个区间叫做函数的增区间。
(2)如图(2)所示,在定义域的某个区间上,若自变量增大时,函数值也随着减小,则称函数在这个区间上是减函数。这个区间叫做函数的减区间。
图(1) 图(2)
几何特征
与增函数相对应的函数图象的变化趋势是:在f(x)为增函数的区间上,函数图象沿x轴的正方向上升。
与减函数相对应的函数图象的变化趋势是:在f(x)为减函数的区间上,函数图象沿x轴的正方向下降。
判定方法
提问:如何判定函数的单调性?
判定函数的单调性有两种方法:借助于函数的图像或根据单调性的定义来判定。
三、巩固知识,例题讲解。
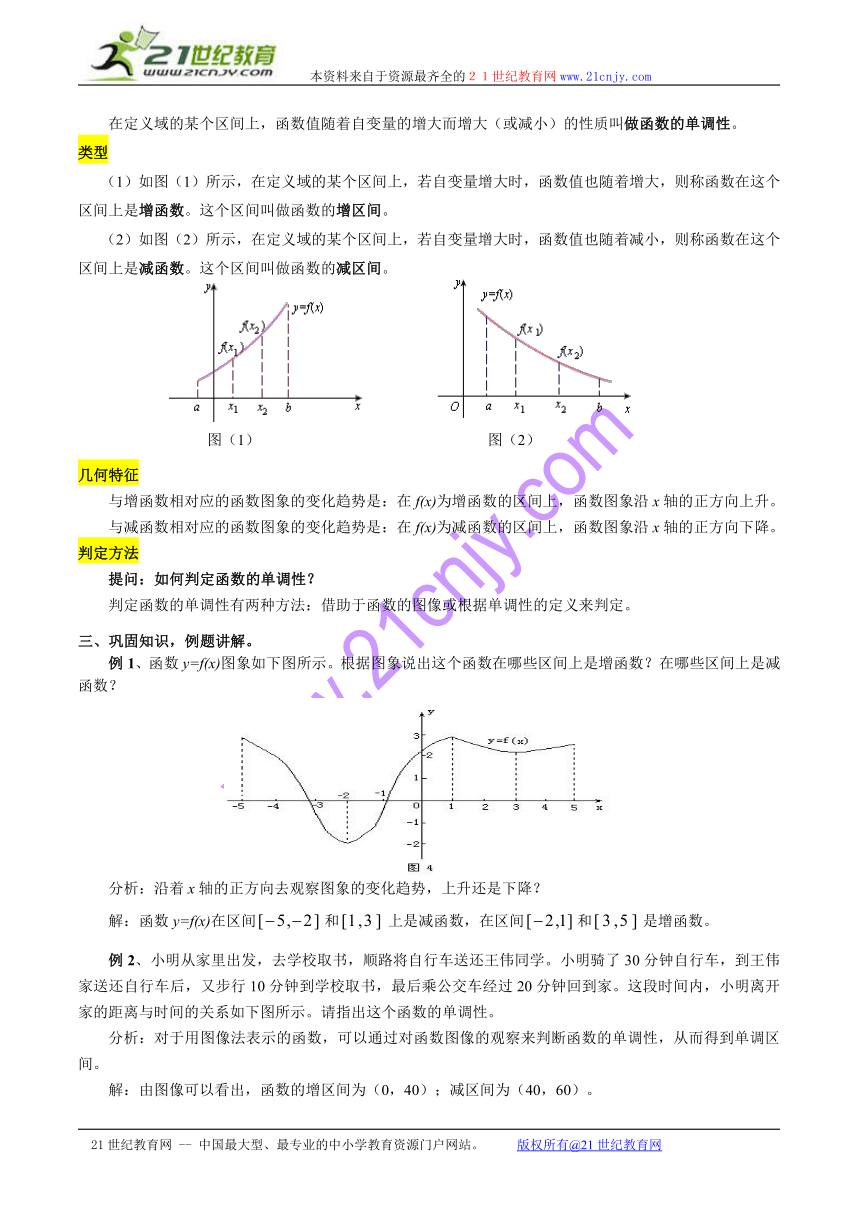
例1、函数y=f(x)图象如下图所示。根据图象说出这个函数在哪些区间上是增函数?在哪些区间上是减函数?
分析:沿着x轴的正方向去观察图象的变化趋势,上升还是下降?
解:函数y=f(x)在区间和上是减函数,在区间和是增函数。
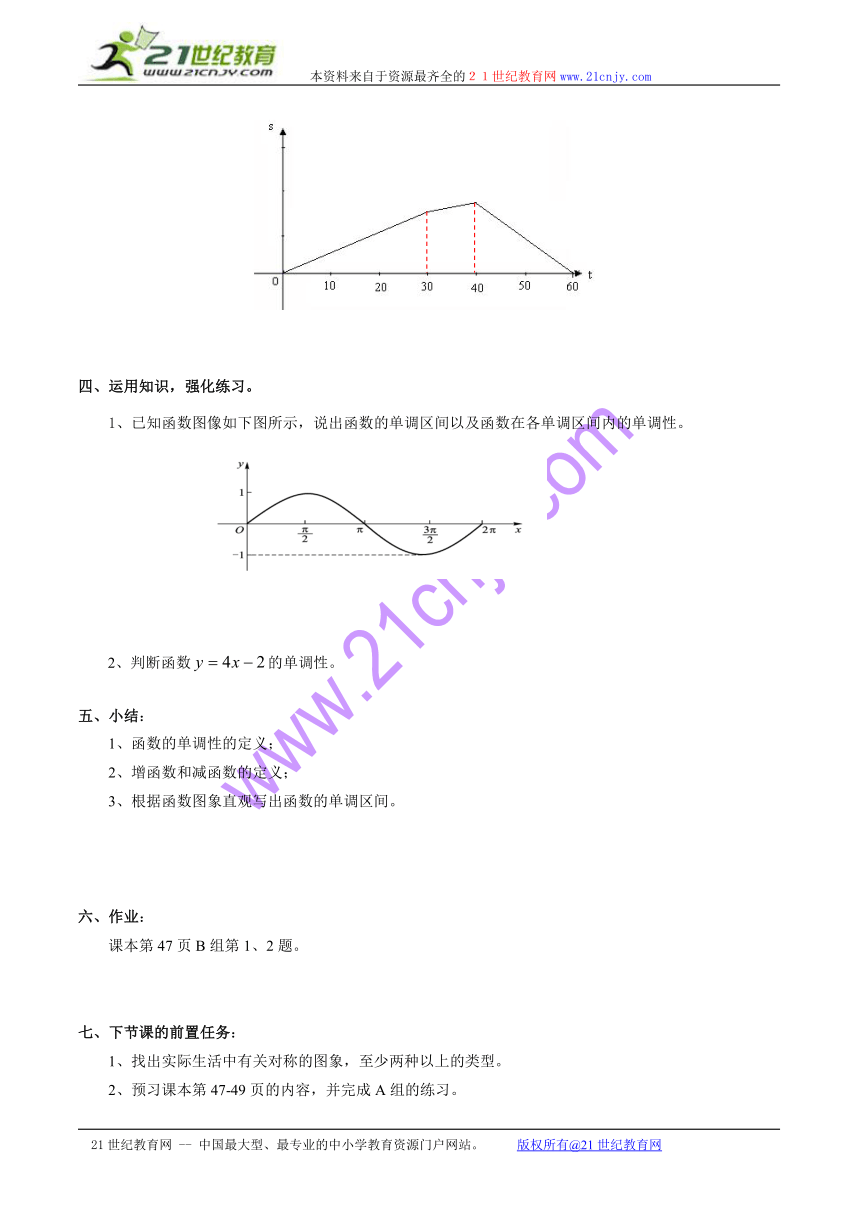
例2、小明从家里出发,去学校取书,顺路将自行车送还王伟同学。小明骑了30分钟自行车,到王伟家送还自行车后,又步行10分钟到学校取书,最后乘公交车经过20分钟回到家。这段时间内,小明离开家的距离与时间的关系如下图所示。请指出这个函数的单调性。
分析:对于用图像法表示的函数,可以通过对函数图像的观察来判断函数的单调性,从而得到单调区间。
解:由图像可以看出,函数的增区间为(0,40);减区间为(40,60)。
四、运用知识,强化练习。
1、已知函数图像如下图所示,说出函数的单调区间以及函数在各单调区间内的单调性。
2、判断函数的单调性。
五、小结:
1、函数的单调性的定义;
2、增函数和减函数的定义;
3、根据函数图象直观写出函数的单调区间。
六、作业:
课本第47页B组第1、2题。
七、下节课的前置任务:
1、找出实际生活中有关对称的图象,至少两种以上的类型。
2、预习课本第47-49页的内容,并完成A组的练习。
一、前置任务。
问题1 :
(1)由于某种原因,2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日,请查阅资料说明做出这个决定的主要原因。
(2)通过查阅历史资料研究北京奥运会开幕式当天的气温变化情况,画出图象。
问题2:下图为股市中,某股票在半天内的行情,请描述此股票的涨幅情况。
二、学习新课。
概念:在定义域的某个区间上,函数值随着自变量的增大而增大(或减小)的性质叫 。
类型
(1)如图(1)所示,在定义域的某个区间上,若自变量增大时,函数值也随着增大,则称函数在这个区间上是 。这个区间叫做函数的 。
(2)如图(2)所示,在定义域的某个区间上,若自变量增大时,函数值也随着减小,则称函数在这个区间上是 。这个区间叫做函数的 。
图(1) 图(2)
几何特征
与增函数相对应的函数图象的变化趋势是:在f(x)为增函数的区间上,函数图象沿x轴的正方向
。
与减函数相对应的函数图象的变化趋势是:在f(x)为减函数的区间上,函数图象沿x轴的正方向
。
判定方法:判定函数的单调性有两种方法:借助于函数的图像或根据单调性的定义来判定。
三、例题讲解。
例1、函数y=f(x)图象如下图所示。根据图象说出这个函数在哪些区间上是增函数?在哪些区间上是减函数?
例2、小明从家里出发,去学校取书,顺路将自行车送还王伟同学。小明骑了30分钟自行车,到王伟家送还自行车后,又步行10分钟到学校取书,最后乘公交车经过20分钟回到家。这段时间内,小明离开家的距离与时间的关系如下图所示。请指出这个函数的单调性。
四、强化练习。
1、已知函数图像如下图所示,说出函数的单调区间以及函数在各单调区间内的单调性。
2、判断函数的单调性。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
【课题】 3.3.3函数的基本性质 —— 单调性
【教学目标】
知识目标:⑴ 理解函数的单调性的概念; ⑵ 会借助于函数图像讨论函数的单调性。
能力目标:通过利用函数图像研究函数性质,培养学生的观察能力。
情感目标:通过生活实例中的问题,让学生感悟数学的实用性。
【教学重点】理解函数单调性的概念及其图像特征,写出函数的单调区间。
【教学难点】抽象出函数单调性的定义。
【教学设计】
(1)用学生熟悉的主题活动将所学的知识有机的结合在一起;
(2)引导学生去感知数学的数形结合思想。通过图形认识特征,由此定义概念,再利用图形(或定义)进行判断;
(3)在问题的思考、交流、解决中培养和发展学生的思维能力。
【教学方法】启发式、探究式、发现式。
【授课班级】09模具(2)班(多媒体1室)
【授课教师】刘其明
【授课时间】第4周星期五第2节(2010年3月19日)
【教学过程】
一、创设情景,兴趣导入,完成前置任务。
问题1
(1)由于某种原因,2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日,请查阅资料说明做出这个决定的主要原因。
(2)通过查阅历史资料研究北京奥运会开幕式当天的气温变化情况,并画出图象。
问题2
下图为股市中,某股票在半天内的行情,请描述此股票的涨幅情况。
归纳
类似地,函数值随着自变量的增大而增大(或减小)的性质就是函数的单调性。
二、动脑思考,探索新知,讲授新课。
概念
在定义域的某个区间上,函数值随着自变量的增大而增大(或减小)的性质叫做函数的单调性。
类型
(1)如图(1)所示,在定义域的某个区间上,若自变量增大时,函数值也随着增大,则称函数在这个区间上是增函数。这个区间叫做函数的增区间。
(2)如图(2)所示,在定义域的某个区间上,若自变量增大时,函数值也随着减小,则称函数在这个区间上是减函数。这个区间叫做函数的减区间。
图(1) 图(2)
几何特征
与增函数相对应的函数图象的变化趋势是:在f(x)为增函数的区间上,函数图象沿x轴的正方向上升。
与减函数相对应的函数图象的变化趋势是:在f(x)为减函数的区间上,函数图象沿x轴的正方向下降。
判定方法
提问:如何判定函数的单调性?
判定函数的单调性有两种方法:借助于函数的图像或根据单调性的定义来判定。
三、巩固知识,例题讲解。
例1、函数y=f(x)图象如下图所示。根据图象说出这个函数在哪些区间上是增函数?在哪些区间上是减函数?
分析:沿着x轴的正方向去观察图象的变化趋势,上升还是下降?
解:函数y=f(x)在区间和上是减函数,在区间和是增函数。
例2、小明从家里出发,去学校取书,顺路将自行车送还王伟同学。小明骑了30分钟自行车,到王伟家送还自行车后,又步行10分钟到学校取书,最后乘公交车经过20分钟回到家。这段时间内,小明离开家的距离与时间的关系如下图所示。请指出这个函数的单调性。
分析:对于用图像法表示的函数,可以通过对函数图像的观察来判断函数的单调性,从而得到单调区间。
解:由图像可以看出,函数的增区间为(0,40);减区间为(40,60)。
四、运用知识,强化练习。
1、已知函数图像如下图所示,说出函数的单调区间以及函数在各单调区间内的单调性。
2、判断函数的单调性。
五、小结:
1、函数的单调性的定义;
2、增函数和减函数的定义;
3、根据函数图象直观写出函数的单调区间。
六、作业:
课本第47页B组第1、2题。
七、下节课的前置任务:
1、找出实际生活中有关对称的图象,至少两种以上的类型。
2、预习课本第47-49页的内容,并完成A组的练习。
一、前置任务。
问题1 :
(1)由于某种原因,2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日,请查阅资料说明做出这个决定的主要原因。
(2)通过查阅历史资料研究北京奥运会开幕式当天的气温变化情况,画出图象。
问题2:下图为股市中,某股票在半天内的行情,请描述此股票的涨幅情况。
二、学习新课。
概念:在定义域的某个区间上,函数值随着自变量的增大而增大(或减小)的性质叫 。
类型
(1)如图(1)所示,在定义域的某个区间上,若自变量增大时,函数值也随着增大,则称函数在这个区间上是 。这个区间叫做函数的 。
(2)如图(2)所示,在定义域的某个区间上,若自变量增大时,函数值也随着减小,则称函数在这个区间上是 。这个区间叫做函数的 。
图(1) 图(2)
几何特征
与增函数相对应的函数图象的变化趋势是:在f(x)为增函数的区间上,函数图象沿x轴的正方向
。
与减函数相对应的函数图象的变化趋势是:在f(x)为减函数的区间上,函数图象沿x轴的正方向
。
判定方法:判定函数的单调性有两种方法:借助于函数的图像或根据单调性的定义来判定。
三、例题讲解。
例1、函数y=f(x)图象如下图所示。根据图象说出这个函数在哪些区间上是增函数?在哪些区间上是减函数?
例2、小明从家里出发,去学校取书,顺路将自行车送还王伟同学。小明骑了30分钟自行车,到王伟家送还自行车后,又步行10分钟到学校取书,最后乘公交车经过20分钟回到家。这段时间内,小明离开家的距离与时间的关系如下图所示。请指出这个函数的单调性。
四、强化练习。
1、已知函数图像如下图所示,说出函数的单调区间以及函数在各单调区间内的单调性。
2、判断函数的单调性。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
