11.1.3三角形的稳定性同步练习
文档属性
| 名称 | 11.1.3三角形的稳定性同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-01 21:17:24 | ||
图片预览



文档简介
11.1.3 三角形的稳定性
一、基 础 题 训 练
1.下列图形中具有稳定性的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
C.长方形的四个角都是直角 D.三角形的稳定性
2.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
(第2题图) (第3题图) (第4题图) (第5题图)
A.两点之间的线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形有稳定性
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 性.
5.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A、C两点之间 B.E、G两点之间 C.B、F两点之间 D.G、H两点之间
6.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是 .
(第6题图) (第7题图)
7.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是 .
二、中 档 题 训 练
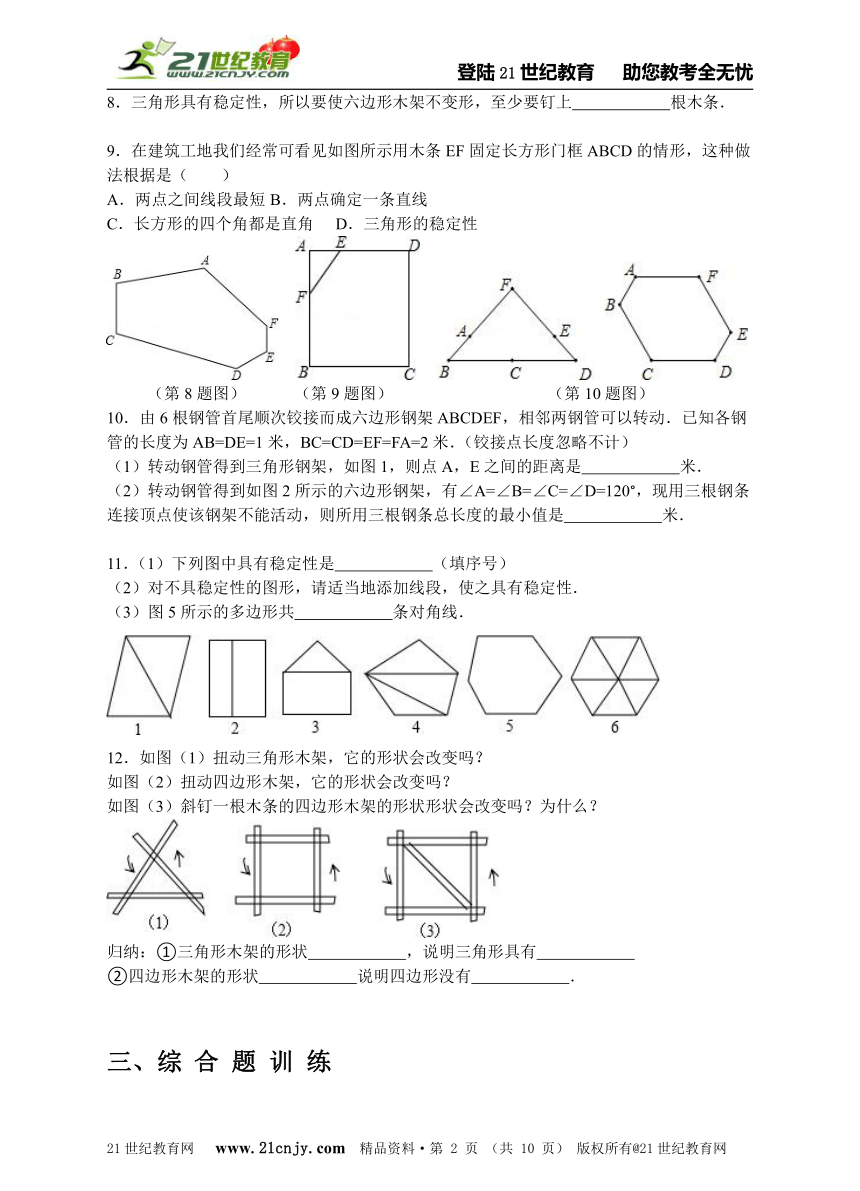
8.三角形具有稳定性,所以要使六边形木架不变形,至少要钉上 根木条.
9.在建筑工地我们经常可看见如图所示用木条EF固定长方形门框ABCD的情形,这种做法根据是( )
A.两点之间线段最短 B.两点确定一条直线
C.长方形的四个角都是直角 D.三角形的稳定性
(第8题图) (第9题图) (第10题图)
10.由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.
11.(1)下列图中具有稳定性是 (填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
(3)图5所示的多边形共 条对角线.
12.如图(1)扭动三角形木架,它的形状会改变吗?
如图(2)扭动四边形木架,它的形状会改变吗?
如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?
归纳:①三角形木架的形状 ,说明三角形具有
②四边形木架的形状 说明四边形没有 .
三、综 合 题 训 练
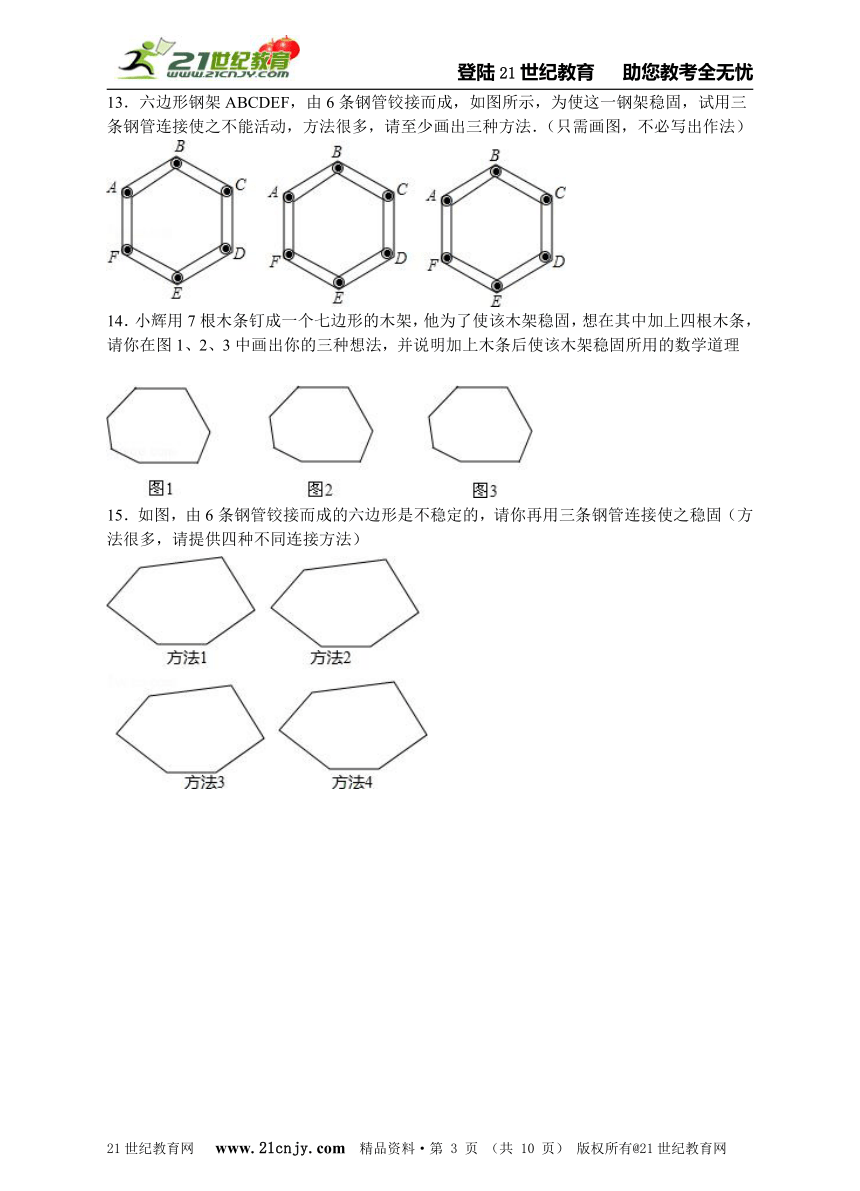
13.六边形钢架ABCDEF,由6条钢管铰接而成,如图所示,为使这一钢架稳固,试用三条钢管连接使之不能活动,方法很多,请至少画出三种方法.(只需画图,不必写出作法)
14.小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理21教育网
15.如图,由6条钢管铰接而成的六边形是不稳定的,请你再用三条钢管连接使之稳固(方法很多,请提供四种不同连接方法)21·cn·jy·com
2如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( A )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
考点 三角形的稳定性.21世纪教育网
解析 根据加上窗钩,可以构成三角形的形状,故可用三角形的稳定性解释.
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( D )
A.两点之间的线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形有稳定性
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 稳定 性.
考点 三角形的稳定性.21世纪教育网
5.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(B )
A.A、C两点之间 B.E、G两点之间 C.B、F两点之间 D.G、H两点之间
考点 三角形的稳定性.21世纪教育网
解析工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.故选B.本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.2·1·c·n·j·y
6.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是 利用三角形的稳定性 .【来源:21·世纪·教育·网】
7.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是 三角形的稳定性 .
考点 三角形的稳定性.21世纪教育网
解析 一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是三角形的稳定性.故应填:三角形的稳定性.本题考查三角形的稳定性在实际生活中的应用问题.
8.三角形具有稳定性,所以要使六边形木架不变形,至少要钉上 3 根木条.
9.(2016春?故城县期末)在建筑工地我们经常可看见如图所示用木条EF固定长方形门框ABCD的情形,这种做法根据是( D )21·世纪*教育网
A.两点之间线段最短 B.两点确定一条直线
C.长方形的四个角都是直角 D.三角形的稳定性
考点 三角形的稳定性.21世纪教育网
解析 根据三角形的稳定性,可直接选择.加上EF后,原图形中具有△AEF了,故这种做法根据的是三角形的稳定性.www-2-1-cnjy-com
故选D.本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
10.由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 3 米.
考点 三角形的稳定性.21世纪教育网
(1)如图1中,∵FB=DF,FA=FE,
∴∠FAE=∠FEA,∠B=∠D,
∴∠FAE=∠B,
∴AE∥BD,
∴=,
∴=,
∴AE=,
故答案为.
(2)如图中,作BN⊥FA于N,延长AB、DC交于点M,连接BD、AD、BF、CF.
在RT△BFN中,∵∠BNF=90°,BN=,FN=AN+AF=+2=,
∴BF==,同理得到AC=DF=,
∵∠ABC=∠BCD=120°,
∴∠MBC=∠MCB=60°,
∴∠M=60°,
∴CM=BC=BM,
∵∠M+∠MAF=180°,
∴AF∥DM,∵AF=CM,
∴四边形AMCF是平行四边形,
∴CF=AM=3,
∵∠BCM=∠CBD+∠CDB=60°,∠CBD=∠CDB,
∴∠CBD=∠CDB=30°,∵∠M=60°,
∴∠MBD=90°,
∴连接AC、BF、DF即可,
∴所用三根钢条总长度的最小值3,
故答案为3.
点评 本题考查三角形的稳定性、平行线的性质、平行四边形的判定和性质、勾股定理.等边三角形的判定和性质等知识,解题的关键是添加辅助线构造特殊三角形以及平行四边形,属于中考常考题型.21世纪教育网版权所有
11.(1)下列图中具有稳定性是 ①④⑥ (填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
(3)图5所示的多边形共 9 条对角线.
(1)具有稳定性的是①④⑥三个.
(2)如图所示:
(3)六边形的对角线有=9条,
故答案为:①④⑥,9.
12.如图(1)扭动三角形木架,它的形状会改变吗?
如图(2)扭动四边形木架,它的形状会改变吗?
如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?
归纳:①三角形木架的形状 是三角形 ,说明三角形具有 稳定性
②四边形木架的形状 四边形 说明四边形没有 不稳定性 .
考点 三角形的稳定性.21世纪教育网
13.六边形钢架ABCDEF,由6条钢管铰接而成,如图所示,为使这一钢架稳固,试用三条钢管连接使之不能活动,方法很多,请至少画出三种方法.(只需画图,不必写出作法)
考点 三角形的稳定性.21世纪教育网
解析 根据三角形具有稳定性,作六边形的三条对角线,把六边形分成三角形即可.
本题考查了三角形的稳定性,比较简单,利用对角线把六边形分成三角形是解题的关键.
14.小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理21cnjy.com
考点 三角形的稳定性.21世纪教育网
点评 此题主要考查了三角形的稳定性,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.这一特性主要应用在实际生活中.
15.如图,由6条钢管铰接而成的六边形是不稳定的,请你再用三条钢管连接使之稳固(方法很多,请提供四种不同连接方法)www.21-cn-jy.com
考点 三角形的稳定性.21世纪教育网
一、基 础 题 训 练
1.下列图形中具有稳定性的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
C.长方形的四个角都是直角 D.三角形的稳定性
2.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
(第2题图) (第3题图) (第4题图) (第5题图)
A.两点之间的线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形有稳定性
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 性.
5.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A、C两点之间 B.E、G两点之间 C.B、F两点之间 D.G、H两点之间
6.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是 .
(第6题图) (第7题图)
7.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是 .
二、中 档 题 训 练
8.三角形具有稳定性,所以要使六边形木架不变形,至少要钉上 根木条.
9.在建筑工地我们经常可看见如图所示用木条EF固定长方形门框ABCD的情形,这种做法根据是( )
A.两点之间线段最短 B.两点确定一条直线
C.长方形的四个角都是直角 D.三角形的稳定性
(第8题图) (第9题图) (第10题图)
10.由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.
11.(1)下列图中具有稳定性是 (填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
(3)图5所示的多边形共 条对角线.
12.如图(1)扭动三角形木架,它的形状会改变吗?
如图(2)扭动四边形木架,它的形状会改变吗?
如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?
归纳:①三角形木架的形状 ,说明三角形具有
②四边形木架的形状 说明四边形没有 .
三、综 合 题 训 练
13.六边形钢架ABCDEF,由6条钢管铰接而成,如图所示,为使这一钢架稳固,试用三条钢管连接使之不能活动,方法很多,请至少画出三种方法.(只需画图,不必写出作法)
14.小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理21教育网
15.如图,由6条钢管铰接而成的六边形是不稳定的,请你再用三条钢管连接使之稳固(方法很多,请提供四种不同连接方法)21·cn·jy·com
2如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( A )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
考点 三角形的稳定性.21世纪教育网
解析 根据加上窗钩,可以构成三角形的形状,故可用三角形的稳定性解释.
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( D )
A.两点之间的线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形有稳定性
4.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 稳定 性.
考点 三角形的稳定性.21世纪教育网
5.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(B )
A.A、C两点之间 B.E、G两点之间 C.B、F两点之间 D.G、H两点之间
考点 三角形的稳定性.21世纪教育网
解析工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.故选B.本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.2·1·c·n·j·y
6.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是 利用三角形的稳定性 .【来源:21·世纪·教育·网】
7.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是 三角形的稳定性 .
考点 三角形的稳定性.21世纪教育网
解析 一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是三角形的稳定性.故应填:三角形的稳定性.本题考查三角形的稳定性在实际生活中的应用问题.
8.三角形具有稳定性,所以要使六边形木架不变形,至少要钉上 3 根木条.
9.(2016春?故城县期末)在建筑工地我们经常可看见如图所示用木条EF固定长方形门框ABCD的情形,这种做法根据是( D )21·世纪*教育网
A.两点之间线段最短 B.两点确定一条直线
C.长方形的四个角都是直角 D.三角形的稳定性
考点 三角形的稳定性.21世纪教育网
解析 根据三角形的稳定性,可直接选择.加上EF后,原图形中具有△AEF了,故这种做法根据的是三角形的稳定性.www-2-1-cnjy-com
故选D.本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
10.由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 3 米.
考点 三角形的稳定性.21世纪教育网
(1)如图1中,∵FB=DF,FA=FE,
∴∠FAE=∠FEA,∠B=∠D,
∴∠FAE=∠B,
∴AE∥BD,
∴=,
∴=,
∴AE=,
故答案为.
(2)如图中,作BN⊥FA于N,延长AB、DC交于点M,连接BD、AD、BF、CF.
在RT△BFN中,∵∠BNF=90°,BN=,FN=AN+AF=+2=,
∴BF==,同理得到AC=DF=,
∵∠ABC=∠BCD=120°,
∴∠MBC=∠MCB=60°,
∴∠M=60°,
∴CM=BC=BM,
∵∠M+∠MAF=180°,
∴AF∥DM,∵AF=CM,
∴四边形AMCF是平行四边形,
∴CF=AM=3,
∵∠BCM=∠CBD+∠CDB=60°,∠CBD=∠CDB,
∴∠CBD=∠CDB=30°,∵∠M=60°,
∴∠MBD=90°,
∴连接AC、BF、DF即可,
∴所用三根钢条总长度的最小值3,
故答案为3.
点评 本题考查三角形的稳定性、平行线的性质、平行四边形的判定和性质、勾股定理.等边三角形的判定和性质等知识,解题的关键是添加辅助线构造特殊三角形以及平行四边形,属于中考常考题型.21世纪教育网版权所有
11.(1)下列图中具有稳定性是 ①④⑥ (填序号)
(2)对不具稳定性的图形,请适当地添加线段,使之具有稳定性.
(3)图5所示的多边形共 9 条对角线.
(1)具有稳定性的是①④⑥三个.
(2)如图所示:
(3)六边形的对角线有=9条,
故答案为:①④⑥,9.
12.如图(1)扭动三角形木架,它的形状会改变吗?
如图(2)扭动四边形木架,它的形状会改变吗?
如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?
归纳:①三角形木架的形状 是三角形 ,说明三角形具有 稳定性
②四边形木架的形状 四边形 说明四边形没有 不稳定性 .
考点 三角形的稳定性.21世纪教育网
13.六边形钢架ABCDEF,由6条钢管铰接而成,如图所示,为使这一钢架稳固,试用三条钢管连接使之不能活动,方法很多,请至少画出三种方法.(只需画图,不必写出作法)
考点 三角形的稳定性.21世纪教育网
解析 根据三角形具有稳定性,作六边形的三条对角线,把六边形分成三角形即可.
本题考查了三角形的稳定性,比较简单,利用对角线把六边形分成三角形是解题的关键.
14.小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理21cnjy.com
考点 三角形的稳定性.21世纪教育网
点评 此题主要考查了三角形的稳定性,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.这一特性主要应用在实际生活中.
15.如图,由6条钢管铰接而成的六边形是不稳定的,请你再用三条钢管连接使之稳固(方法很多,请提供四种不同连接方法)www.21-cn-jy.com
考点 三角形的稳定性.21世纪教育网
