11.2.1三角形的内角(1)同步练习
文档属性
| 名称 | 11.2.1三角形的内角(1)同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 353.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-02 00:00:00 | ||
图片预览



文档简介
11.2.1 三角形的内角
一、基 础 题 训 练
1.已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.正三角形
2.如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为( )
A.60° B.70° C.80° D.85°
(第2题图) (第4题图)
3.(2016春?太康县期中)在△ABC中,若∠A=80°,∠B=∠C,则∠C= 度.
4.(2016春?江阴市期中)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
(1)图1中的∠ABC的度数为 .
(2)图2中已知AE∥BC,则∠AFD的度数为 .
5.如图所示,BE平分∠ABC,DE∥BC,若∠AED=40°,∠BEC=110°,则∠ADE= 度.21cnjy.com
(第5题图) (第6题图)
6.如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
(1)若∠A=50°,求∠BOC的度数;
(2)若∠A=n°,求∠BOC的度数.
二、中 档 题 训 练
7.三角形的内角和等于( )
A.90° B.180° C.300° D.360°
8.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= .21*cnjy*com
9.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
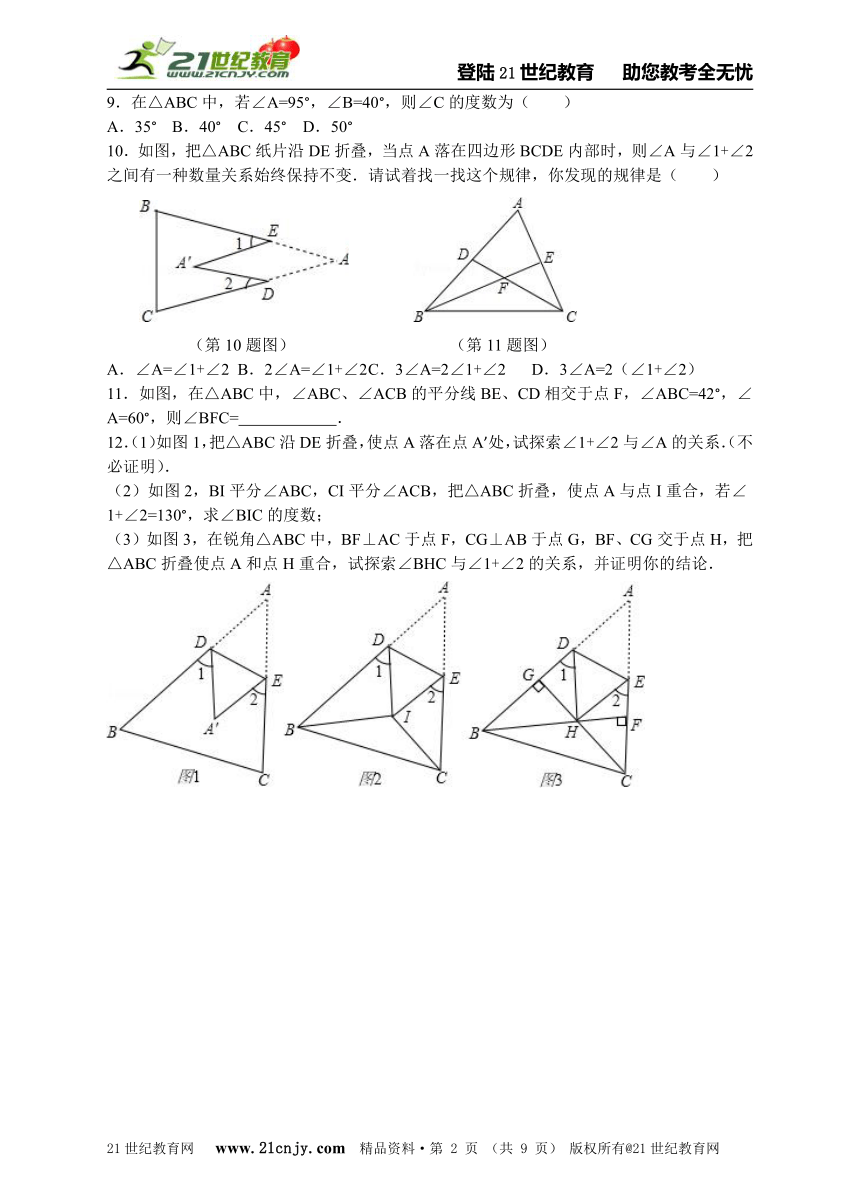
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
(第10题图) (第11题图)
A.∠A=∠1+∠2 B.2∠A=∠1+∠2 C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
11.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= .21·cn·jy·com
12.(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明).
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
三、综 合 题 训 练
13.如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,
∠BED=70°.求∠ABC和∠BAC的度数.
14.如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
15.如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
参考答案与试题解析
1.已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是( A )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.正三角形网版权所有
2.如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为( C )
A.60° B.70° C.80° D.85°
考点 三角形的外角性质;余角和补角;三角形内角和定理.21世纪教育网
3.在△ABC中,若∠A=80°,∠B=∠C,则∠C= 50 度.21世纪教育网
解析 由三角形内角和定理可知.
∵∠A=80°,∠B=∠C,∠A+∠B+∠C=180°,
∴80°+2∠C=180°,
∴∠C=50°.
4.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:【来源:21·世纪·教育·网】
(1)图1中的∠ABC的度数为 75° .
(2)图2中已知AE∥BC,则∠AFD的度数为 75° .
考点 三角形内角和定理;平行线的性质.21世纪教育网
2)∵∠B=60°,∠BAC=90°,
∴∠C=30°,
∵AE∥BC,
∴∠CAE=∠C=30°,
∴∠AFD=∠CAE+∠E=30°+45°=75°.
5.如图所示,BE平分∠ABC,DE∥BC,若∠AED=40°,∠BEC=110°,则∠ADE= 60 度. 21*cnjy*com
考点 三角形内角和定理;角平分线的定义;平行线的性质.21世纪教育网
本题利用了:①三角形内角和定理;②角的平分线的性质;③两直线平行,同旁内角互补.
6.如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
(1)若∠A=50°,求∠BOC的度数;
(2)若∠A=n°,求∠BOC的度数.
考点 三角形内角和定理;三角形的外角性质.21世纪教育网
解析 (1)根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后根据三角形的内角和定理列式计算即可得解;www.21-cn-jy.com
(2)与(1)的思路相同求解即可.
(1)∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×130°=65°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°;
7.三角形的内角和等于( B )
A.90° B.180° C.300° D.360°
解析 利用三角形的内角和定理:三角形的内角和为180°即可解本题
8.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= 110° .2·1·c·n·j·y
版权所有
解析 由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70°,再利用三角形内角和定理即可求出∠BDC的度数.21·世纪*教育网
∵D点是∠ABC和∠ACB角平分线的交点,
∴∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠DBC+∠DCB=70°,
∴∠BDC=180°﹣70°=110°,
9.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为(C )
A.35° B.40° C.45° D.50°21世纪教育网
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2 C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
考点 三角形内角和定理;翻折变换(折叠问题).21世纪教育网
11.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= 120° .【来源:21cnj*y.co*m】
21世纪教育网
解析 由∠ABC=42°,∠A=60°,根据三角形内角和等于180°,可得∠ACB的度数,又因为∠ABC、∠ACB的平分线分别为BE、CD,所以可以求得∠FBC和∠FCB的度数,从而求得∠BFC的度数.【出处:21教育名师】
∵∠ABC=42°,∠A=60°,∠ABC+∠A+∠ACB=180°.
∴∠ACB=180°﹣42°﹣60°=78°.
又∵∠ABC、∠ACB的平分线分别为BE、CD.
∴∠FBC=,∠FCB=.
又∵∠FBC+∠FCB+∠BFC=180°.
∴∠BFC=180°﹣21°﹣39°=120°.
12.(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明).21教育网
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;www-2-1-cnjy-com
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
考点 三角形内角和定理;翻折变换(折叠问题).21世纪教育网
(2)由(1)∠1+∠2=2∠A,得2∠A=130°,∴∠A=65°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=(∠ABC+∠ACB)
=(180°﹣∠A)=90°﹣∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB),
=180°﹣(90°﹣∠A)=90°+×65°=122.5°;
(3)∵BF⊥AC,CG⊥AB,∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,∴∠BHC=∠FHG=180°﹣∠A,由(1)知∠1+∠2=2∠A,
∴∠A=(∠1+∠2),
∴∠BHC=180°﹣(∠1+∠2).
正确的利用翻折变换的性质得出对应关系是解决问题的关键.
13.如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.2-1-c-n-j-y
21世纪教育网
解析 先根据AD是△ABC的高得出∠ADB=90°,再由三角形内角和定理及三角形外角的性质可知∠DBE+∠ADB+∠BED=180°,故∠DBE=180°﹣∠ADB﹣∠BED=20°.根据BE平分∠ABC得出∠ABC=2∠DBE=40°. 根据∠BAC+∠ABC+∠C=180°,∠C=60°即可得出结论.【版权所有:21教育】
∵AD是△ABC的高,
∴∠ADB=90°.
14.如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
21世纪教育网
(2)∵DE⊥AC,
∴∠CED=90°,
∴∠EDC=90°﹣∠C=14°.
本题考查了三角形的角平分线、中线和高的相关知识;利用三角形的内角和求得∠BAC的度数是正确解答本题的关键.21世纪教育网版权所有
15.如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.21教育名师原创作品
考点 三角形的角平分线、中线和高.21世纪教育网
解析 先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠BAE=∠BAC,而∠BAD=90°﹣∠B,然后利用∠DAE=∠BAE﹣∠BAD进行计算即可.
在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣60°=90°
∵AD是的角平分线
∴∠BAE=∠BAC=45°,
一、基 础 题 训 练
1.已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.正三角形
2.如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为( )
A.60° B.70° C.80° D.85°
(第2题图) (第4题图)
3.(2016春?太康县期中)在△ABC中,若∠A=80°,∠B=∠C,则∠C= 度.
4.(2016春?江阴市期中)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
(1)图1中的∠ABC的度数为 .
(2)图2中已知AE∥BC,则∠AFD的度数为 .
5.如图所示,BE平分∠ABC,DE∥BC,若∠AED=40°,∠BEC=110°,则∠ADE= 度.21cnjy.com
(第5题图) (第6题图)
6.如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
(1)若∠A=50°,求∠BOC的度数;
(2)若∠A=n°,求∠BOC的度数.
二、中 档 题 训 练
7.三角形的内角和等于( )
A.90° B.180° C.300° D.360°
8.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= .21*cnjy*com
9.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
(第10题图) (第11题图)
A.∠A=∠1+∠2 B.2∠A=∠1+∠2 C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
11.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= .21·cn·jy·com
12.(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明).
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
三、综 合 题 训 练
13.如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,
∠BED=70°.求∠ABC和∠BAC的度数.
14.如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
15.如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
参考答案与试题解析
1.已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是( A )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.正三角形网版权所有
2.如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为( C )
A.60° B.70° C.80° D.85°
考点 三角形的外角性质;余角和补角;三角形内角和定理.21世纪教育网
3.在△ABC中,若∠A=80°,∠B=∠C,则∠C= 50 度.21世纪教育网
解析 由三角形内角和定理可知.
∵∠A=80°,∠B=∠C,∠A+∠B+∠C=180°,
∴80°+2∠C=180°,
∴∠C=50°.
4.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:【来源:21·世纪·教育·网】
(1)图1中的∠ABC的度数为 75° .
(2)图2中已知AE∥BC,则∠AFD的度数为 75° .
考点 三角形内角和定理;平行线的性质.21世纪教育网
2)∵∠B=60°,∠BAC=90°,
∴∠C=30°,
∵AE∥BC,
∴∠CAE=∠C=30°,
∴∠AFD=∠CAE+∠E=30°+45°=75°.
5.如图所示,BE平分∠ABC,DE∥BC,若∠AED=40°,∠BEC=110°,则∠ADE= 60 度. 21*cnjy*com
考点 三角形内角和定理;角平分线的定义;平行线的性质.21世纪教育网
本题利用了:①三角形内角和定理;②角的平分线的性质;③两直线平行,同旁内角互补.
6.如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
(1)若∠A=50°,求∠BOC的度数;
(2)若∠A=n°,求∠BOC的度数.
考点 三角形内角和定理;三角形的外角性质.21世纪教育网
解析 (1)根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后根据三角形的内角和定理列式计算即可得解;www.21-cn-jy.com
(2)与(1)的思路相同求解即可.
(1)∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×130°=65°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°;
7.三角形的内角和等于( B )
A.90° B.180° C.300° D.360°
解析 利用三角形的内角和定理:三角形的内角和为180°即可解本题
8.如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= 110° .2·1·c·n·j·y
版权所有
解析 由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70°,再利用三角形内角和定理即可求出∠BDC的度数.21·世纪*教育网
∵D点是∠ABC和∠ACB角平分线的交点,
∴∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠DBC+∠DCB=70°,
∴∠BDC=180°﹣70°=110°,
9.在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为(C )
A.35° B.40° C.45° D.50°21世纪教育网
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2 C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
考点 三角形内角和定理;翻折变换(折叠问题).21世纪教育网
11.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC= 120° .【来源:21cnj*y.co*m】
21世纪教育网
解析 由∠ABC=42°,∠A=60°,根据三角形内角和等于180°,可得∠ACB的度数,又因为∠ABC、∠ACB的平分线分别为BE、CD,所以可以求得∠FBC和∠FCB的度数,从而求得∠BFC的度数.【出处:21教育名师】
∵∠ABC=42°,∠A=60°,∠ABC+∠A+∠ACB=180°.
∴∠ACB=180°﹣42°﹣60°=78°.
又∵∠ABC、∠ACB的平分线分别为BE、CD.
∴∠FBC=,∠FCB=.
又∵∠FBC+∠FCB+∠BFC=180°.
∴∠BFC=180°﹣21°﹣39°=120°.
12.(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明).21教育网
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;www-2-1-cnjy-com
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
考点 三角形内角和定理;翻折变换(折叠问题).21世纪教育网
(2)由(1)∠1+∠2=2∠A,得2∠A=130°,∴∠A=65°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=(∠ABC+∠ACB)
=(180°﹣∠A)=90°﹣∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB),
=180°﹣(90°﹣∠A)=90°+×65°=122.5°;
(3)∵BF⊥AC,CG⊥AB,∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,∴∠BHC=∠FHG=180°﹣∠A,由(1)知∠1+∠2=2∠A,
∴∠A=(∠1+∠2),
∴∠BHC=180°﹣(∠1+∠2).
正确的利用翻折变换的性质得出对应关系是解决问题的关键.
13.如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.2-1-c-n-j-y
21世纪教育网
解析 先根据AD是△ABC的高得出∠ADB=90°,再由三角形内角和定理及三角形外角的性质可知∠DBE+∠ADB+∠BED=180°,故∠DBE=180°﹣∠ADB﹣∠BED=20°.根据BE平分∠ABC得出∠ABC=2∠DBE=40°. 根据∠BAC+∠ABC+∠C=180°,∠C=60°即可得出结论.【版权所有:21教育】
∵AD是△ABC的高,
∴∠ADB=90°.
14.如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
21世纪教育网
(2)∵DE⊥AC,
∴∠CED=90°,
∴∠EDC=90°﹣∠C=14°.
本题考查了三角形的角平分线、中线和高的相关知识;利用三角形的内角和求得∠BAC的度数是正确解答本题的关键.21世纪教育网版权所有
15.如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.21教育名师原创作品
考点 三角形的角平分线、中线和高.21世纪教育网
解析 先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠BAE=∠BAC,而∠BAD=90°﹣∠B,然后利用∠DAE=∠BAE﹣∠BAD进行计算即可.
在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣60°=90°
∵AD是的角平分线
∴∠BAE=∠BAC=45°,
