勾股定理变式题
图片预览


文档简介
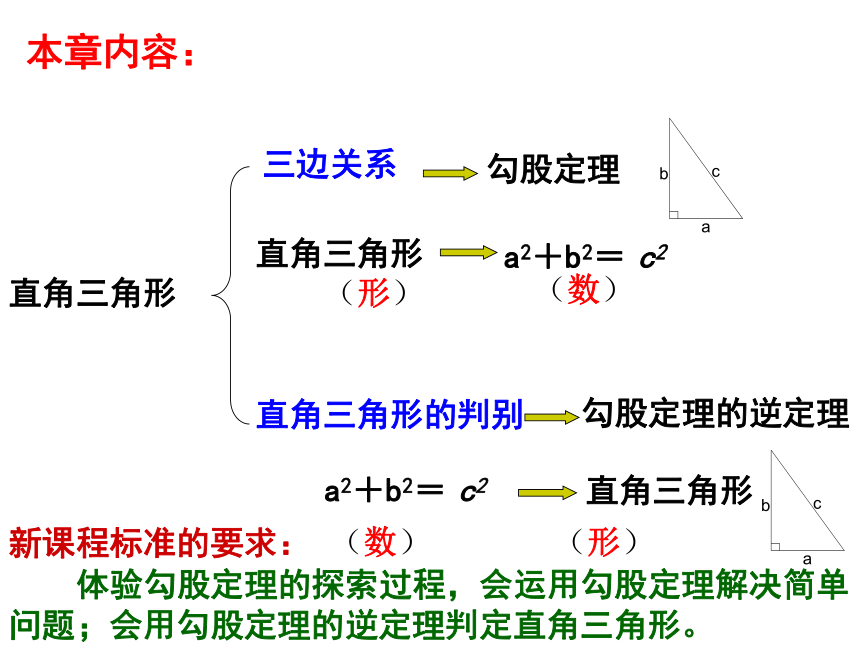
课件31张PPT。 《勾股定理》 教材例习题变式本章内容:三边关系直角三角形的判别(形)(数)(形)(数) 体验勾股定理的探索过程,会运用勾股定理解决简单问题;会用勾股定理的逆定理判定直角三角形。 新课程标准的要求:勾股定理的逆定理 一、教材113页习题19.1
1.求出下列直角三角形中未知边的长度.变式1. ∠C=90°,a=6,b=8,则c=_______.
变式2.已知一直角三角形的两直角边比为3︰4,斜边长为10,求这个三角形的面积?变式3.已知一直角三角形的面积为24,两直角边比为3︰4求这个三角形斜边长? 这类问题是勾股定理应用的较为重要的题型,问题的实质就是已知直角三角形两边,求第三边。通过变式帮助学生掌握问题实质,构建数学模型。变式4.已知一直角三角形的两条边长分别为6和8,求第三边的长?变式5.已知一直角三角形的两条边长分别为6和8,求这个三角形的面积?变式6.等腰△ABC的两边长为10和12,求底边上的高。 渗透分类讨论的思想。通过变式帮助学生掌握问题实质,构建数学模型。
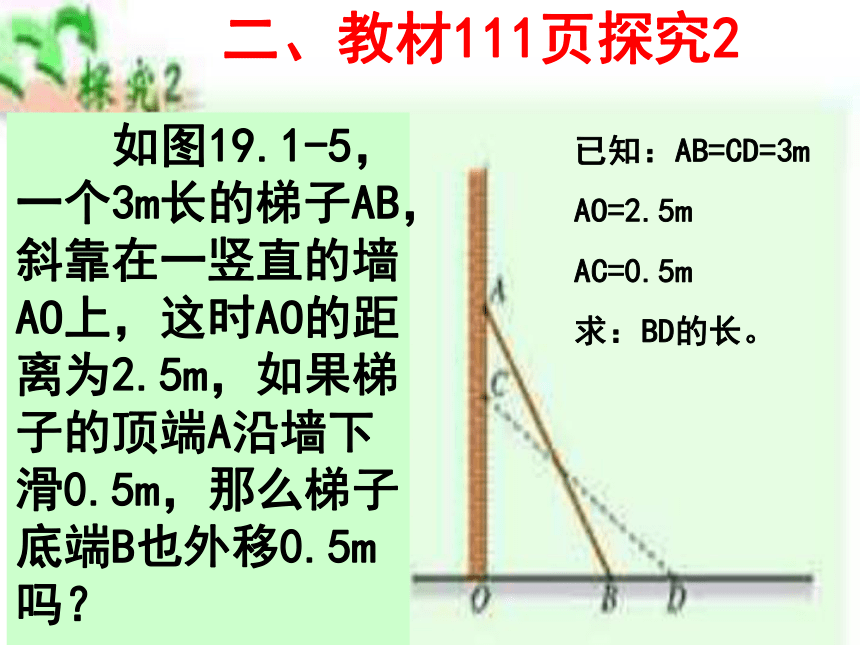
如图19.1-5,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
二、教材111页探究2
已知:AB=CD=3m
AO=2.5m
AC=0.5m
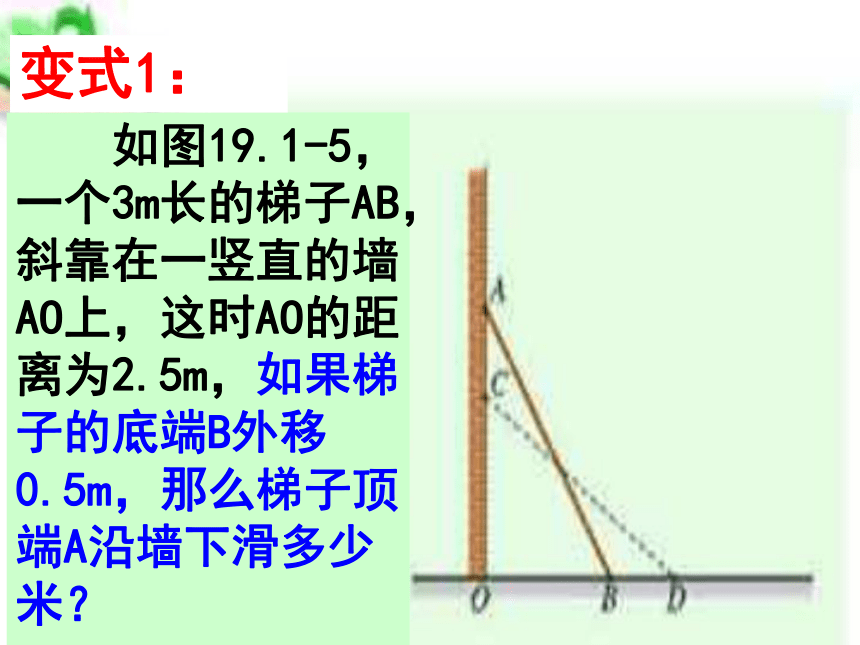
求:BD的长。 如图19.1-5,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的底端B外移0.5m,那么梯子顶端A沿墙下滑多少米?
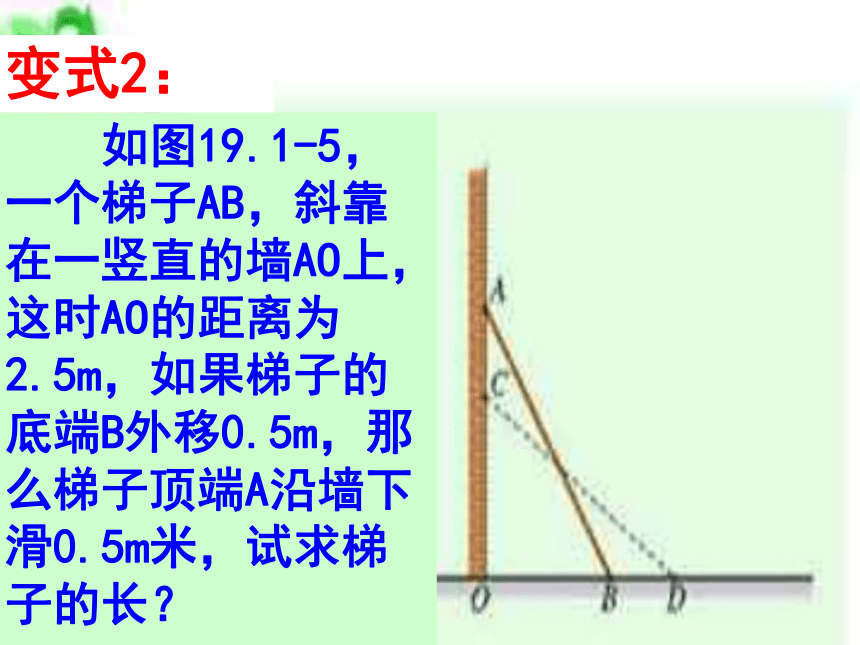
变式1: 如图19.1-5,一个梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的底端B外移0.5m,那么梯子顶端A沿墙下滑0.5m米,试求梯子的长?
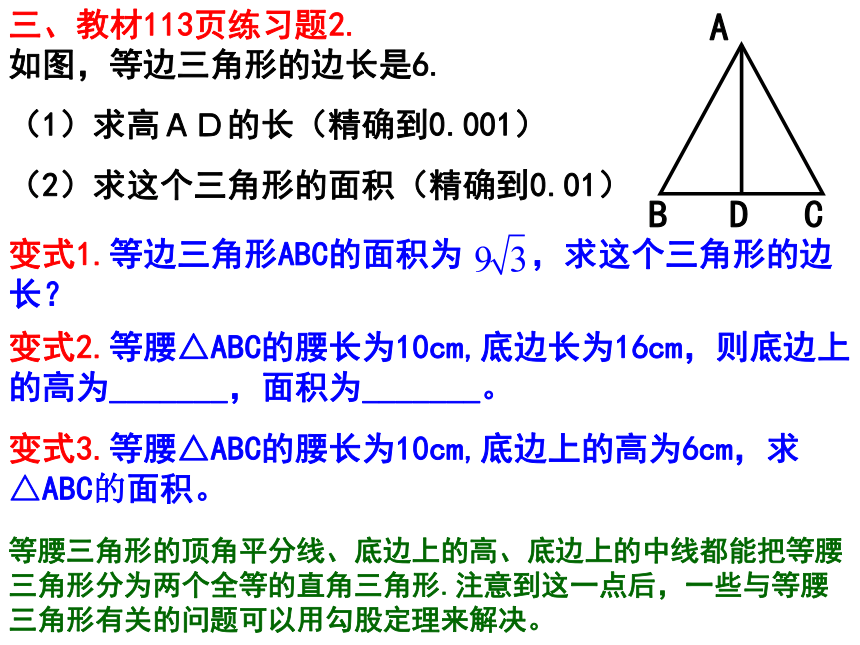
变式2:三、教材113页练习题2. 如图,等边三角形的边长是6.
(1)求高AD的长(精确到0.001)
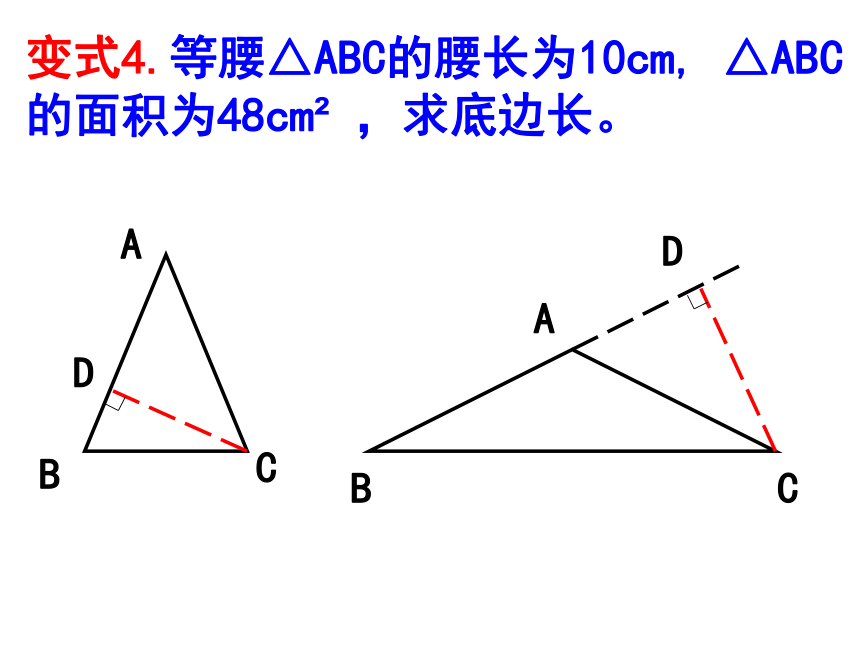
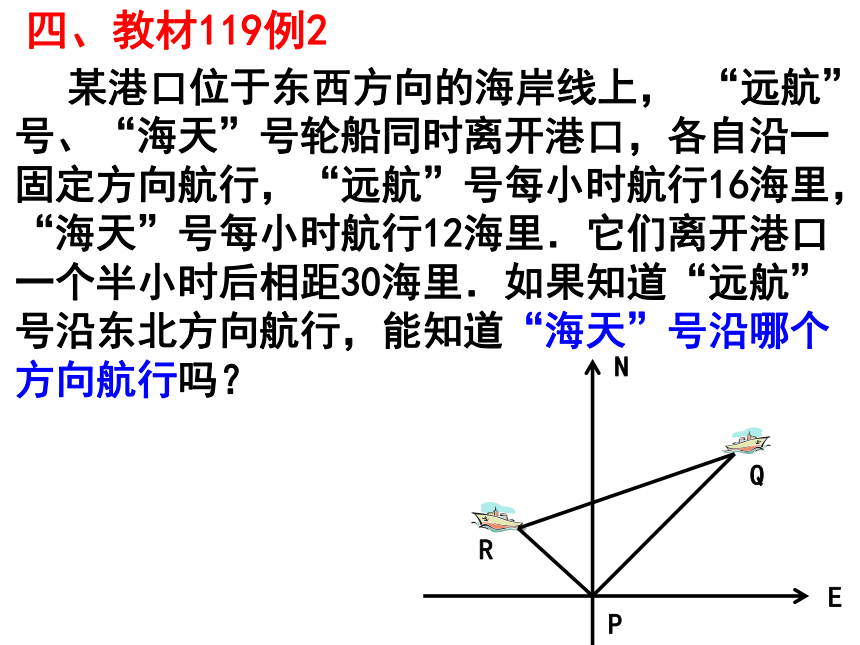
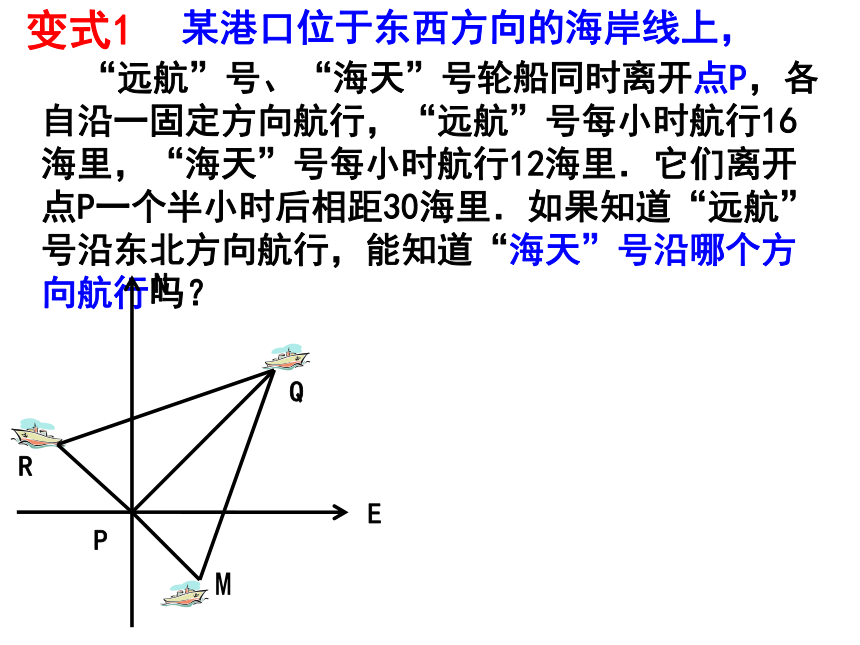
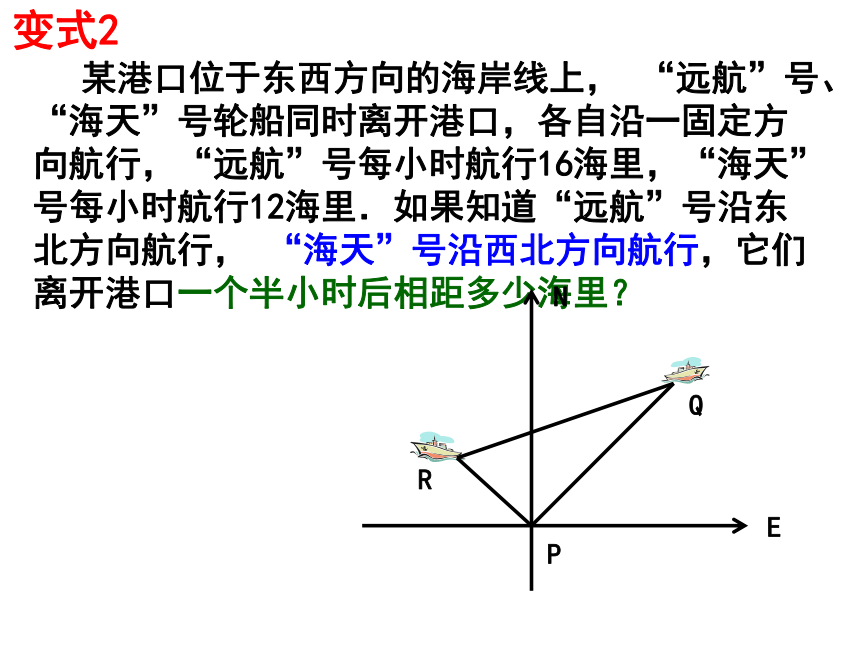
(2)求这个三角形的面积(精确到0.01)变式2.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为_______,面积为_______。变式3.等腰△ABC的腰长为10cm,底边上的高为6cm,求△ABC的面积。等腰三角形的顶角平分线、底边上的高、底边上的中线都能把等腰三角形分为两个全等的直角三角形.注意到这一点后,一些与等腰三角形有关的问题可以用勾股定理来解决。变式4.等腰△ABC的腰长为10cm, △ABC的面积为48cm2 ,求底边长。ACBDCDAB 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?四、教材119例2 “远航”号、“海天”号轮船同时离开点P,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开点P一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?变式1某港口位于东西方向的海岸线上, 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.如果知道“远航”号沿东北方向航行, “海天”号沿西北方向航行,它们离开港口一个半小时后相距多少海里?变式2 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,如果知道“远航”号沿东北方向航行, “海天”号沿西北方向航行,它们离开港口一个半小时后相距30海里, 问“海天”号每小时航行多少海里?变式3 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行, “海天”号沿西北方向航行,“远航”号与“海天”号行驶的速度比为3︰4,求“远航”号与“海天”号行驶的路程?变式5求“远航”号或“海天”
号行驶的速度是多少?变式4 1.如图,南北向MN为我国海界,MN以西为我国领海,以东为公海.上午9时50分,我反走私艇A发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海? ··12135通过以上变式训练,学生易于解决其他类似习题:2.两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?甲(A)乙(B)┏3.一艘轮船以20海里/小时的速度离开港口O向东北方向航行,另一艘轮船同时以22海里/小时的速度离开港口向东南方向航行,2小时后两船相距多远?甲(A)乙(B)┏ 4.轮船A以24千米/时的速度离开港口向东北方向航行,轮船B同时离开港口以一定的速度向西北方向航行,它们离开港口2小时后测得两船的距离为52千米,求轮船B的速度是多少? ABC五、教材125页复习题19拓广探索8题
已知圆柱的底面半径为6cm,高为10cm,蚂蚁从A点爬到B点的最短路程是多少(精确到0.1cm)?C变式1:
有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至C,(A,C在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是多少?CBADCCA变式2:有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?ABAC 变式3:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?C 变式4:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?ACFGHD分析:有3种情况,六条路线。(1)经过前面和上底面; (或经过下面和下底面)(2)经过前面和右面; (或经过左面和后面)(3)经过左面和上底面. (或经过下底面和右面) 如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少? 勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形。尝试把立体图形转换为平面图形。 谢 谢 !
1.求出下列直角三角形中未知边的长度.变式1. ∠C=90°,a=6,b=8,则c=_______.
变式2.已知一直角三角形的两直角边比为3︰4,斜边长为10,求这个三角形的面积?变式3.已知一直角三角形的面积为24,两直角边比为3︰4求这个三角形斜边长? 这类问题是勾股定理应用的较为重要的题型,问题的实质就是已知直角三角形两边,求第三边。通过变式帮助学生掌握问题实质,构建数学模型。变式4.已知一直角三角形的两条边长分别为6和8,求第三边的长?变式5.已知一直角三角形的两条边长分别为6和8,求这个三角形的面积?变式6.等腰△ABC的两边长为10和12,求底边上的高。 渗透分类讨论的思想。通过变式帮助学生掌握问题实质,构建数学模型。
如图19.1-5,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
二、教材111页探究2
已知:AB=CD=3m
AO=2.5m
AC=0.5m
求:BD的长。 如图19.1-5,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的底端B外移0.5m,那么梯子顶端A沿墙下滑多少米?
变式1: 如图19.1-5,一个梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的底端B外移0.5m,那么梯子顶端A沿墙下滑0.5m米,试求梯子的长?
变式2:三、教材113页练习题2. 如图,等边三角形的边长是6.
(1)求高AD的长(精确到0.001)
(2)求这个三角形的面积(精确到0.01)变式2.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为_______,面积为_______。变式3.等腰△ABC的腰长为10cm,底边上的高为6cm,求△ABC的面积。等腰三角形的顶角平分线、底边上的高、底边上的中线都能把等腰三角形分为两个全等的直角三角形.注意到这一点后,一些与等腰三角形有关的问题可以用勾股定理来解决。变式4.等腰△ABC的腰长为10cm, △ABC的面积为48cm2 ,求底边长。ACBDCDAB 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?四、教材119例2 “远航”号、“海天”号轮船同时离开点P,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开点P一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?变式1某港口位于东西方向的海岸线上, 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.如果知道“远航”号沿东北方向航行, “海天”号沿西北方向航行,它们离开港口一个半小时后相距多少海里?变式2 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,如果知道“远航”号沿东北方向航行, “海天”号沿西北方向航行,它们离开港口一个半小时后相距30海里, 问“海天”号每小时航行多少海里?变式3 某港口位于东西方向的海岸线上, “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行, “海天”号沿西北方向航行,“远航”号与“海天”号行驶的速度比为3︰4,求“远航”号与“海天”号行驶的路程?变式5求“远航”号或“海天”
号行驶的速度是多少?变式4 1.如图,南北向MN为我国海界,MN以西为我国领海,以东为公海.上午9时50分,我反走私艇A发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海? ··12135通过以上变式训练,学生易于解决其他类似习题:2.两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?甲(A)乙(B)┏3.一艘轮船以20海里/小时的速度离开港口O向东北方向航行,另一艘轮船同时以22海里/小时的速度离开港口向东南方向航行,2小时后两船相距多远?甲(A)乙(B)┏ 4.轮船A以24千米/时的速度离开港口向东北方向航行,轮船B同时离开港口以一定的速度向西北方向航行,它们离开港口2小时后测得两船的距离为52千米,求轮船B的速度是多少? ABC五、教材125页复习题19拓广探索8题
已知圆柱的底面半径为6cm,高为10cm,蚂蚁从A点爬到B点的最短路程是多少(精确到0.1cm)?C变式1:
有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至C,(A,C在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是多少?CBADCCA变式2:有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?ABAC 变式3:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?C 变式4:如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?ACFGHD分析:有3种情况,六条路线。(1)经过前面和上底面; (或经过下面和下底面)(2)经过前面和右面; (或经过左面和后面)(3)经过左面和上底面. (或经过下底面和右面) 如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少? 勾股定理在生活中的应用十分广泛,利用勾股定理解决问题,关键是找出问题中隐藏的直角三角形或自己构造合适的直角三角形。尝试把立体图形转换为平面图形。 谢 谢 !
