平面直角坐标系学案
图片预览




文档简介
重庆古南中学导学图系列 数学七年级第六章 平面直角坐标系
导学图(1)§6.1.1 有序数对 自主学习
带刻度的直尺.
1. 有顺序的两个数a、b组成的数对叫做 __ ,记作___,注意(a、b)中的a、b的____不能改变.
2.写出下列各点的有序数对A( 5 , 2 );
B( , );C( , );
D( , );E( , );
F( , );G( , );
H( , );I( , )。
知识总结
“有序数对”记作(a,b).有序:是指(a,b)与(b,a)是两个不同的数对;数对:是指必须由两个数才能确定.
三. 师生合作探究,解决问题:
探索一:
小刚、小英、小明的家在同一栋楼房中,小刚的家是9楼2号,我们用(9,2)表示;
(1) 小英的家是12楼5号,用(5,12)表示对吗 如果不对该如何表示.
(2) (16,7)表示小明的家,那么小明的家是几楼几号.
分析:根据9楼2号用(9,2)表示,可得第一个数表示楼层数,第二个数表示号数.
探索二:
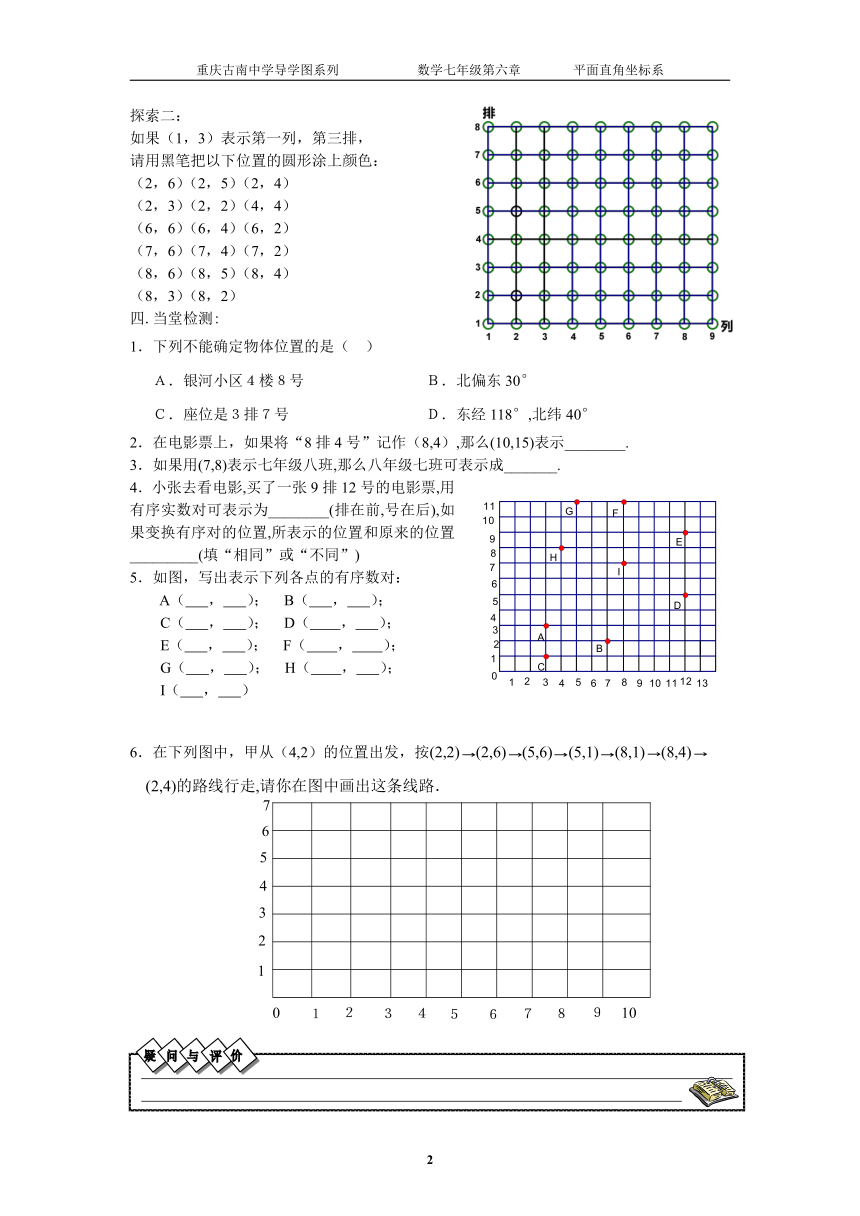
如果(1,3)表示第一列,第三排,
请用黑笔把以下位置的圆形涂上颜色:
(2,6)(2,5)(2,4)
(2,3)(2,2)(4,4)
(6,6)(6,4)(6,2)
(7,6)(7,4)(7,2)
(8,6)(8,5)(8,4)
(8,3)(8,2)
四.当堂检测:
1.下列不能确定物体位置的是( )
A.银河小区4楼8号 B.北偏东30°
C.座位是3排7号 D.东经118°,北纬40°
2.在电影票上,如果将“8排4号”记作(8,4),那么(10,15)表示________.
3.如果用(7,8)表示七年级八班,那么八年级七班可表示成_______.
4.小张去看电影,买了一张9排12号的电影票,用有序实数对可表示为________(排在前,号在后),如果变换有序对的位置,所表示的位置和原来的位置_________(填“相同”或“不同”)
5.如图,写出表示下列各点的有序数对:
A( , ); B( , );
C( , ); D( , );
E( , ); F( , );
G( , ); H( , );
I( , )
6.在下列图中,甲从(4,2)的位置出发,按(2,2) (2,6) (5,6) (5,1) (8,1) (8,4)
(2,4)的路线行走,请你在图中画出这条线路.
导学图(2)§6.1.2平面直角坐标系(1) 自主学习
带刻度的直尺.
1.数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的 .
例如点A在数轴上的坐标为 ,点B在数轴上的坐标为 。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
2.在平面内画两条互相垂直、原点重合的数轴组成 。水平的数轴称为 或 ,习惯上取向 方向为正方向,竖直的数轴称为 或 ,取向 方向为正方向;
两坐标轴的交点为平面直角坐标系的 。
3.在平面直角坐标系中平面内的一点可以用一个
来表示,这个有序数对就是该点的 。
4.在平面直角坐标系中由点A分别向x轴和y轴做垂线,垂足M在x轴上的坐标是 ,则横坐标是 ,垂足N在y轴上的坐标是 ,则纵坐标是 ;则点A的坐标记作A( , )
5.在平面直角坐标系中由点B分别向x轴和y轴做垂线,B的横坐标是 ,B的纵坐标是 ;则点B的坐标记作B( , )
三.师生合作探究,解决问题:
探索一:
如图,写出其中标有字母的各点的坐标,并指出它们的横坐标和纵坐标:
探索二:在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.并观察所得的图形,你觉得它象什么?
①A(0 , 6), B(-4, 3), C(4 , 3)
②D(-2 , 3), E(-2 , -3),F (2 , -3), G(2 , 3)
探索三:在如图的直角坐标系中写出下列各点的坐标.你能发现什么规律
探索二 探索三
发现规律:x轴上的点的纵坐标为 ,表示为( , )
y轴上的点的横坐标为 ,表示为( , )
四.当堂检测:
1、点A(0,-1)的位置在平面直角坐标系的 轴上。
2、在直角坐标中,A点的位置为(-3,2),B点的位置是(3,2),连接A、B两点所成的线段与 平行。
3、若点N(a+5,a-2)在x轴上,则点N的坐标为 。
4、已知点M(2,-3),则M到x轴的距离为 ,到y轴的距离为 。
5、已知点P到x轴和y轴的距离分别是2和5,则P点的坐标为 。
导学图(3)§6.1.2平面直角坐标系(2) 自主学习
带刻度的直尺.
1.在平面内画两条互相垂直、原点重合的数轴组成 。水平的数轴称为 或 ,竖直的数轴称为 或 ,两坐标轴的交点为平面直角坐标系的 。
2.建立平面直角坐标系后,坐标平面就被两条 坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做 、 、 、 。
注意坐标轴上的点不属于 。
3.根据点所在的位置,用“+”“-”或“0”填表。
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
4.下列各点分别在坐标平面的什么位置上?
A(3,2) ; B(0,-2) ;
C(-3,-2) ; D(-3,0) ;
E(-1.5,3.5) ; F(2,-3) 。
三.师生合作探究,解决问题:
探索一:在方格纸上分别描出下列点的坐标,看看 这些点在什么位置上,由此你有什么发现?
(1)A(2,3) , B(2,-1) , C(2,4) , D(2,0) E(2,-3) , F(2,-4)
(2)M(-1,3) , N(0,3) , P(-3,3) , Q(3,3)
解: 如图所示,可以发现(1)A(2,3) ,B(2,-1) , C(2,4) , D(2,0) , E(2,-3) , F(2,-4)的横坐标都是 ,结果:它们在一条与 轴平行的直线上.
(2)M(-1,3) , N(0,3) , P(-3,3) , Q(3,3) 的纵坐标都是 ,结果: 它们在一条与 轴平行的直线上.
探索二:
如图, 矩形ABCD的长宽分别是6 , 4 , (1) 分别以两对边中点的连线为x轴,y轴建立直角坐标系,并写出各个顶点的坐标.
解:A( , );B( , );
C( , );D( , );
c
点A与点D关于 轴对称;
点A与点B关于 轴对称;
点A与点C关于 对称;
结论:关于X轴对称的两点 坐标相同, 坐标互为相反数;
关于Y轴对称的两点 坐标相同, 坐标互为相反数;
关于原点对称的两点横、纵坐标均互为 ;
(2)请另建立一个适当的直角坐标系,并分别写出A、B、C、D各点的坐标。
导学图(4)§6.2.1用坐标表示地理位置 自主学习
带刻度的直尺.
1.在平面内画两条互相垂直、原点重合的数轴组成 。水平的数轴称为 或 ,竖直的数轴称为 或 ,两坐标轴的交点为平面直角坐标系的 。
2. 用坐标表示地理位置的过程是:
(1)建立坐标系,选择一个 参照点为原点,确定 的正方向。
(2)根据 确定单位长度,并在坐标轴上标出。
(3)在坐标平面内画出这些点,并写出各点的 和各个地点的 。
3.根据以下条件画一副示意图,标出学校和小刚家、小强家、小敏家的位置。
小刚家:出校门向东走150m,再向北走200m.
小强家:出校门向西走200m,再向北走350m,最后向东走50m.
小敏家:出校门向南走100m,再向东走300m,最后向南走75m.
如图,选学校所在位置为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表50m长,依题目所给的条件,点(150,200)就是小刚家的位置。
类似地,请你在图上画出小强家、小敏家的位置,并标明它们的坐标。
三.师生合作探究,解决问题:
探索一: 如图,这是某市部分简图,(1)请以火车站为坐标原点建立平面直角坐标系,并分别写出各地的坐标.(2)如果每个方格的边长是500m,坐车只能走水平方向和竖直方向,那么一个旅客下了火车后要赶到医院,他至少要坐多远的车.
探索二:如图是某校利用平面直角坐标系画出的的地图。如果教学楼和食堂的坐标分别是
(1,2)和(7,3),图书馆的地点是(6,6),你能在此地图上标出图书馆的位置吗?(注:以东西方向为x轴,南北方向为y轴)
四、当堂检测:夏令营举行野外拉练活动,老师交给大家一张地图,如图所示,地图上画了一个直角坐标系,作为定向标记,给出了四座农舍的坐标是(1,2),(-3,4),(3,4),(0,3). 目的地位于连结第一与第三座农舍的直线和连结第二与第四座农舍的直线的交点.利用平面直角坐标系,同学们很快就到达了目的地.请你在图中画出目的地的位置.
导学图(5)§6.2.2用坐标表示平移 自主学习
带刻度的直尺.
1.平移变换不改变图形的 ;2.连结各组对应点的线段 。
2.将点A(-2,-3)向右平移3个单位, 得到点B , 在图上标出这个点,它的坐标为 ,把点A向左平移3个单位,得到点C,在图上标出这个点,它的坐标为
3.把点A向上或向下平移4个单位,观察它们的变化,你能从中发现什么规律吗?
发现的规律:当点A向右平移a个单位时,横坐标 ,纵坐标 ,当点A向左平移a个单位时,则横坐标 ,纵坐标 ,当点A向上平移b个单位时,横坐标 ,纵坐标 ,当点A向下平移b个单位时,横坐标 ,纵坐标 .
结论:在平面直角坐标系中,将点(x , y)向右或(向左)平移a个单位长度,可以得到对应点( , )或 ( , );将点(x , y)向上(或向下平移b个单位长度,可以得到对应点( , )或( , )
4.将点M(1,2)向左平移2个单位后,其坐标为__________。
5.将点N(-1,-2)向上平移3个单位长度后,其坐标为_________.
6.将点A(4,3)向___平移 个单位长度后,其坐标为(-1,3)
7.将点P(-1,2)向右平移3个单位长度,再向下平移4个单位长度后,其坐标变为________.
3. 师生合作探究,解决问题:
探索一:如图,三角形三个顶点的坐标分别A(2,2),B(-2,-1),C(3,-2)
(1)将三角形ABC三个顶点的横坐标都减去3,分别得到各点,并依次连结所得的三角形与三角形ABC的大小,形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去2,分别得到各点,依次连结,所得的三角形与三角形ABC的大小,形状和位置有什么关系?
结论:在平面直角坐标系内,如果把一个图形上的各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;如果把各点的纵坐标都加(或减去)一个正数a,相应的图形就是把原图形向 (或向 )平移 个个单位长度.
四.当堂检测:
将四边形ABCD向左平移2个单位长度,可以得到四边形,画出平移后的图形,并指出其各个顶点的坐标.
导学图(6) 平面直角坐标系全章小结
【学习过程】
1. 复习:
(一)确定平面内点的位置
(二)
坐标轴上点P(x,y) 连线平行于坐标轴的点 点P(x,y)在各象限的坐标特点
x轴 y轴 原点 平行于x轴 平行于y轴 第一象限 第二象限 第三象限 第四象限
(x,o) ( ) ( ) 坐标相同 坐标相同 x>0y>0 x 0y 0 x 0y 0 x 0y 0
(三). 一个图形在平面直角坐标系中进行平移,其坐标就要发生相应的变化, 可以简单地理解为: 左、右平移纵坐标不变,横坐标变,变化规律是左减右加, 上下平移横坐标不变,纵坐标变,变化规律是上加下减。 例如:
当P(x ,y)向右平移a个单位长度,再向上平移b个单位长度后坐标为p′(x+a ,y+b)。
二.当堂检测:
1、原点O的坐标是 ,x轴上的点的坐标的特点是 ,y轴上的点的坐标的特是 ;点M(a,0)在 轴上。
2、点A(﹣1,2)关于y轴的对称点坐标是 ;点A关于原点的对称点的坐标是 。
点A关于x轴对称的点的坐标为
3、已知点M 与点N 关于x轴对称,则x+y= .
4、点P到x轴的距离是2,到y轴的距离是3,则P点的坐标是 。
5、线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为__________。
6、在平面直角坐标系内,把点P(-5,2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是 。
7、将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=_________ 。
8、已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 __________。
9、A(– 3,– 2)、B(2,– 2)、C(– 2,1),D(3,1)是坐标平面内的四个点,则线段AB与CD的关系是_____________。
10 、点A在x轴上,位于原点左侧,距离坐标原点7个单位长度,则此点的坐标为___________
11、在Y轴上且到点A(0,-3)的线段长度是4的点B的坐标为____________
12、在坐标系内,点P(2,-2)和点Q(2,4)之间的距离等于________个单位长度。线段PQ的中点的坐标是___________。
13、已知P点坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是________。
14、已知点A(-3+a,2a+9)在第二象限的角平分线上,则a的值是____________
15、若点B(a,b)在第三象限,则点C(-a+1,3b-5) 在第____________象限。
16、如果点M(x+3,2x-4)在第四象限内,那么x的取值范围是______________。
17、已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于
10,则a的值是__________。
18、已知,则点(m,n)且mn=0则该点在___________。
二、选择题
1、在平面直角坐标系中,点 一定在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2、如果点A(a,.b)在第三象限,则点B(-a+1,3b-5)关于原点的对称点是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、点P(a,b)在第二象限,则点Q(a-1,b+1)在( )
A、 第一象限 B、 第二象限 C、 第三象限 D、第四象限
4、若 ,且点M(a,b)在第二象限,则点M的坐标是( )
A、(5,4) B、(-5,4) C、(-5,-4) D、(5,-4)
5、△DEF(三角形)是由△ABC平移得到的,点A(-1,-4)的对应点为D(1,-1),则点B(1,1)的对应点E、点C(-1,4)的对应点F的坐标分别为( )
A、(2,2),(3,4) B、(3,4),(1,7) C、(-2,2),(1,7) D、(3,4),(2,-2)
6、过A(4,-2)和B(-2,-2)两点的直线一定( )
A、垂直于x轴 B、与Y轴相交但不平于x轴
B、 平行于x轴 D、与x轴、y轴平行
7、已知点A(3a,2b)在x轴上方,在y轴的左边,则点A到轴、轴的距离分别为( )
A、3a,-2b B、-3a,2b C、2b,-3a D、-2b,3a
1.会用有序数对表示点的位置;
2.已知点的位置会用有序数对表示.
学习目标
学习目标
1.认识平面直角坐标系,在给定的直角坐标系中,能由点的位置写出坐标;
2.会由点的坐标在平面直角坐标系中描出该点。
7
6
5
4
3
D
A
1.知道坐标平面被两条坐标轴分成四个象限,并且知道四个象限内点的坐标特征和坐标轴上点的坐标特征。
学习目标
宾馆
体育场
市场
一. P49~P50页
食堂●
教学楼●
B
超市
医院
1. 会建立适当的直角坐标系描述地理位置的方法,体会平面直角坐标系在实际生活中的应用
学习目标
一. P42~P43页
1.理解平移变化性质以及对应点坐标变化的规律.
学习目标
-22
4
3
1
2
x
2
1
0
9
-4
3
2
O
1
-4--4
-33
一. P50~P52页
A
B
D
C
10
8
7
6
5
4
3
2
1
一. P39~P40
第 象限
坐标符号( , )
( )
第 象限
坐标符号( , )
( )
第 象限
坐标符号( , )
( )
建立平面直角坐标系
第 象限
坐标符号(+,+)
(垂直且有公共原点)
(两条数轴)
y
x
1
C
B
A
O
二.独立完成下列作业
二.独立完成下列作业
二.独立完成下列作业
二.独立完成下列作业
二.独立完成下列作业
一. P40~P42
-1
4
-1
-2
-3
火车站
文化馆
11
导学图(1)§6.1.1 有序数对 自主学习
带刻度的直尺.
1. 有顺序的两个数a、b组成的数对叫做 __ ,记作___,注意(a、b)中的a、b的____不能改变.
2.写出下列各点的有序数对A( 5 , 2 );
B( , );C( , );
D( , );E( , );
F( , );G( , );
H( , );I( , )。
知识总结
“有序数对”记作(a,b).有序:是指(a,b)与(b,a)是两个不同的数对;数对:是指必须由两个数才能确定.
三. 师生合作探究,解决问题:
探索一:
小刚、小英、小明的家在同一栋楼房中,小刚的家是9楼2号,我们用(9,2)表示;
(1) 小英的家是12楼5号,用(5,12)表示对吗 如果不对该如何表示.
(2) (16,7)表示小明的家,那么小明的家是几楼几号.
分析:根据9楼2号用(9,2)表示,可得第一个数表示楼层数,第二个数表示号数.
探索二:
如果(1,3)表示第一列,第三排,
请用黑笔把以下位置的圆形涂上颜色:
(2,6)(2,5)(2,4)
(2,3)(2,2)(4,4)
(6,6)(6,4)(6,2)
(7,6)(7,4)(7,2)
(8,6)(8,5)(8,4)
(8,3)(8,2)
四.当堂检测:
1.下列不能确定物体位置的是( )
A.银河小区4楼8号 B.北偏东30°
C.座位是3排7号 D.东经118°,北纬40°
2.在电影票上,如果将“8排4号”记作(8,4),那么(10,15)表示________.
3.如果用(7,8)表示七年级八班,那么八年级七班可表示成_______.
4.小张去看电影,买了一张9排12号的电影票,用有序实数对可表示为________(排在前,号在后),如果变换有序对的位置,所表示的位置和原来的位置_________(填“相同”或“不同”)
5.如图,写出表示下列各点的有序数对:
A( , ); B( , );
C( , ); D( , );
E( , ); F( , );
G( , ); H( , );
I( , )
6.在下列图中,甲从(4,2)的位置出发,按(2,2) (2,6) (5,6) (5,1) (8,1) (8,4)
(2,4)的路线行走,请你在图中画出这条线路.
导学图(2)§6.1.2平面直角坐标系(1) 自主学习
带刻度的直尺.
1.数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的 .
例如点A在数轴上的坐标为 ,点B在数轴上的坐标为 。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
2.在平面内画两条互相垂直、原点重合的数轴组成 。水平的数轴称为 或 ,习惯上取向 方向为正方向,竖直的数轴称为 或 ,取向 方向为正方向;
两坐标轴的交点为平面直角坐标系的 。
3.在平面直角坐标系中平面内的一点可以用一个
来表示,这个有序数对就是该点的 。
4.在平面直角坐标系中由点A分别向x轴和y轴做垂线,垂足M在x轴上的坐标是 ,则横坐标是 ,垂足N在y轴上的坐标是 ,则纵坐标是 ;则点A的坐标记作A( , )
5.在平面直角坐标系中由点B分别向x轴和y轴做垂线,B的横坐标是 ,B的纵坐标是 ;则点B的坐标记作B( , )
三.师生合作探究,解决问题:
探索一:
如图,写出其中标有字母的各点的坐标,并指出它们的横坐标和纵坐标:
探索二:在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.并观察所得的图形,你觉得它象什么?
①A(0 , 6), B(-4, 3), C(4 , 3)
②D(-2 , 3), E(-2 , -3),F (2 , -3), G(2 , 3)
探索三:在如图的直角坐标系中写出下列各点的坐标.你能发现什么规律
探索二 探索三
发现规律:x轴上的点的纵坐标为 ,表示为( , )
y轴上的点的横坐标为 ,表示为( , )
四.当堂检测:
1、点A(0,-1)的位置在平面直角坐标系的 轴上。
2、在直角坐标中,A点的位置为(-3,2),B点的位置是(3,2),连接A、B两点所成的线段与 平行。
3、若点N(a+5,a-2)在x轴上,则点N的坐标为 。
4、已知点M(2,-3),则M到x轴的距离为 ,到y轴的距离为 。
5、已知点P到x轴和y轴的距离分别是2和5,则P点的坐标为 。
导学图(3)§6.1.2平面直角坐标系(2) 自主学习
带刻度的直尺.
1.在平面内画两条互相垂直、原点重合的数轴组成 。水平的数轴称为 或 ,竖直的数轴称为 或 ,两坐标轴的交点为平面直角坐标系的 。
2.建立平面直角坐标系后,坐标平面就被两条 坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做 、 、 、 。
注意坐标轴上的点不属于 。
3.根据点所在的位置,用“+”“-”或“0”填表。
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
4.下列各点分别在坐标平面的什么位置上?
A(3,2) ; B(0,-2) ;
C(-3,-2) ; D(-3,0) ;
E(-1.5,3.5) ; F(2,-3) 。
三.师生合作探究,解决问题:
探索一:在方格纸上分别描出下列点的坐标,看看 这些点在什么位置上,由此你有什么发现?
(1)A(2,3) , B(2,-1) , C(2,4) , D(2,0) E(2,-3) , F(2,-4)
(2)M(-1,3) , N(0,3) , P(-3,3) , Q(3,3)
解: 如图所示,可以发现(1)A(2,3) ,B(2,-1) , C(2,4) , D(2,0) , E(2,-3) , F(2,-4)的横坐标都是 ,结果:它们在一条与 轴平行的直线上.
(2)M(-1,3) , N(0,3) , P(-3,3) , Q(3,3) 的纵坐标都是 ,结果: 它们在一条与 轴平行的直线上.
探索二:
如图, 矩形ABCD的长宽分别是6 , 4 , (1) 分别以两对边中点的连线为x轴,y轴建立直角坐标系,并写出各个顶点的坐标.
解:A( , );B( , );
C( , );D( , );
c
点A与点D关于 轴对称;
点A与点B关于 轴对称;
点A与点C关于 对称;
结论:关于X轴对称的两点 坐标相同, 坐标互为相反数;
关于Y轴对称的两点 坐标相同, 坐标互为相反数;
关于原点对称的两点横、纵坐标均互为 ;
(2)请另建立一个适当的直角坐标系,并分别写出A、B、C、D各点的坐标。
导学图(4)§6.2.1用坐标表示地理位置 自主学习
带刻度的直尺.
1.在平面内画两条互相垂直、原点重合的数轴组成 。水平的数轴称为 或 ,竖直的数轴称为 或 ,两坐标轴的交点为平面直角坐标系的 。
2. 用坐标表示地理位置的过程是:
(1)建立坐标系,选择一个 参照点为原点,确定 的正方向。
(2)根据 确定单位长度,并在坐标轴上标出。
(3)在坐标平面内画出这些点,并写出各点的 和各个地点的 。
3.根据以下条件画一副示意图,标出学校和小刚家、小强家、小敏家的位置。
小刚家:出校门向东走150m,再向北走200m.
小强家:出校门向西走200m,再向北走350m,最后向东走50m.
小敏家:出校门向南走100m,再向东走300m,最后向南走75m.
如图,选学校所在位置为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表50m长,依题目所给的条件,点(150,200)就是小刚家的位置。
类似地,请你在图上画出小强家、小敏家的位置,并标明它们的坐标。
三.师生合作探究,解决问题:
探索一: 如图,这是某市部分简图,(1)请以火车站为坐标原点建立平面直角坐标系,并分别写出各地的坐标.(2)如果每个方格的边长是500m,坐车只能走水平方向和竖直方向,那么一个旅客下了火车后要赶到医院,他至少要坐多远的车.
探索二:如图是某校利用平面直角坐标系画出的的地图。如果教学楼和食堂的坐标分别是
(1,2)和(7,3),图书馆的地点是(6,6),你能在此地图上标出图书馆的位置吗?(注:以东西方向为x轴,南北方向为y轴)
四、当堂检测:夏令营举行野外拉练活动,老师交给大家一张地图,如图所示,地图上画了一个直角坐标系,作为定向标记,给出了四座农舍的坐标是(1,2),(-3,4),(3,4),(0,3). 目的地位于连结第一与第三座农舍的直线和连结第二与第四座农舍的直线的交点.利用平面直角坐标系,同学们很快就到达了目的地.请你在图中画出目的地的位置.
导学图(5)§6.2.2用坐标表示平移 自主学习
带刻度的直尺.
1.平移变换不改变图形的 ;2.连结各组对应点的线段 。
2.将点A(-2,-3)向右平移3个单位, 得到点B , 在图上标出这个点,它的坐标为 ,把点A向左平移3个单位,得到点C,在图上标出这个点,它的坐标为
3.把点A向上或向下平移4个单位,观察它们的变化,你能从中发现什么规律吗?
发现的规律:当点A向右平移a个单位时,横坐标 ,纵坐标 ,当点A向左平移a个单位时,则横坐标 ,纵坐标 ,当点A向上平移b个单位时,横坐标 ,纵坐标 ,当点A向下平移b个单位时,横坐标 ,纵坐标 .
结论:在平面直角坐标系中,将点(x , y)向右或(向左)平移a个单位长度,可以得到对应点( , )或 ( , );将点(x , y)向上(或向下平移b个单位长度,可以得到对应点( , )或( , )
4.将点M(1,2)向左平移2个单位后,其坐标为__________。
5.将点N(-1,-2)向上平移3个单位长度后,其坐标为_________.
6.将点A(4,3)向___平移 个单位长度后,其坐标为(-1,3)
7.将点P(-1,2)向右平移3个单位长度,再向下平移4个单位长度后,其坐标变为________.
3. 师生合作探究,解决问题:
探索一:如图,三角形三个顶点的坐标分别A(2,2),B(-2,-1),C(3,-2)
(1)将三角形ABC三个顶点的横坐标都减去3,分别得到各点,并依次连结所得的三角形与三角形ABC的大小,形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去2,分别得到各点,依次连结,所得的三角形与三角形ABC的大小,形状和位置有什么关系?
结论:在平面直角坐标系内,如果把一个图形上的各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;如果把各点的纵坐标都加(或减去)一个正数a,相应的图形就是把原图形向 (或向 )平移 个个单位长度.
四.当堂检测:
将四边形ABCD向左平移2个单位长度,可以得到四边形,画出平移后的图形,并指出其各个顶点的坐标.
导学图(6) 平面直角坐标系全章小结
【学习过程】
1. 复习:
(一)确定平面内点的位置
(二)
坐标轴上点P(x,y) 连线平行于坐标轴的点 点P(x,y)在各象限的坐标特点
x轴 y轴 原点 平行于x轴 平行于y轴 第一象限 第二象限 第三象限 第四象限
(x,o) ( ) ( ) 坐标相同 坐标相同 x>0y>0 x 0y 0 x 0y 0 x 0y 0
(三). 一个图形在平面直角坐标系中进行平移,其坐标就要发生相应的变化, 可以简单地理解为: 左、右平移纵坐标不变,横坐标变,变化规律是左减右加, 上下平移横坐标不变,纵坐标变,变化规律是上加下减。 例如:
当P(x ,y)向右平移a个单位长度,再向上平移b个单位长度后坐标为p′(x+a ,y+b)。
二.当堂检测:
1、原点O的坐标是 ,x轴上的点的坐标的特点是 ,y轴上的点的坐标的特是 ;点M(a,0)在 轴上。
2、点A(﹣1,2)关于y轴的对称点坐标是 ;点A关于原点的对称点的坐标是 。
点A关于x轴对称的点的坐标为
3、已知点M 与点N 关于x轴对称,则x+y= .
4、点P到x轴的距离是2,到y轴的距离是3,则P点的坐标是 。
5、线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为__________。
6、在平面直角坐标系内,把点P(-5,2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是 。
7、将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=_________ 。
8、已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 __________。
9、A(– 3,– 2)、B(2,– 2)、C(– 2,1),D(3,1)是坐标平面内的四个点,则线段AB与CD的关系是_____________。
10 、点A在x轴上,位于原点左侧,距离坐标原点7个单位长度,则此点的坐标为___________
11、在Y轴上且到点A(0,-3)的线段长度是4的点B的坐标为____________
12、在坐标系内,点P(2,-2)和点Q(2,4)之间的距离等于________个单位长度。线段PQ的中点的坐标是___________。
13、已知P点坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是________。
14、已知点A(-3+a,2a+9)在第二象限的角平分线上,则a的值是____________
15、若点B(a,b)在第三象限,则点C(-a+1,3b-5) 在第____________象限。
16、如果点M(x+3,2x-4)在第四象限内,那么x的取值范围是______________。
17、已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于
10,则a的值是__________。
18、已知,则点(m,n)且mn=0则该点在___________。
二、选择题
1、在平面直角坐标系中,点 一定在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2、如果点A(a,.b)在第三象限,则点B(-a+1,3b-5)关于原点的对称点是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、点P(a,b)在第二象限,则点Q(a-1,b+1)在( )
A、 第一象限 B、 第二象限 C、 第三象限 D、第四象限
4、若 ,且点M(a,b)在第二象限,则点M的坐标是( )
A、(5,4) B、(-5,4) C、(-5,-4) D、(5,-4)
5、△DEF(三角形)是由△ABC平移得到的,点A(-1,-4)的对应点为D(1,-1),则点B(1,1)的对应点E、点C(-1,4)的对应点F的坐标分别为( )
A、(2,2),(3,4) B、(3,4),(1,7) C、(-2,2),(1,7) D、(3,4),(2,-2)
6、过A(4,-2)和B(-2,-2)两点的直线一定( )
A、垂直于x轴 B、与Y轴相交但不平于x轴
B、 平行于x轴 D、与x轴、y轴平行
7、已知点A(3a,2b)在x轴上方,在y轴的左边,则点A到轴、轴的距离分别为( )
A、3a,-2b B、-3a,2b C、2b,-3a D、-2b,3a
1.会用有序数对表示点的位置;
2.已知点的位置会用有序数对表示.
学习目标
学习目标
1.认识平面直角坐标系,在给定的直角坐标系中,能由点的位置写出坐标;
2.会由点的坐标在平面直角坐标系中描出该点。
7
6
5
4
3
D
A
1.知道坐标平面被两条坐标轴分成四个象限,并且知道四个象限内点的坐标特征和坐标轴上点的坐标特征。
学习目标
宾馆
体育场
市场
一. P49~P50页
食堂●
教学楼●
B
超市
医院
1. 会建立适当的直角坐标系描述地理位置的方法,体会平面直角坐标系在实际生活中的应用
学习目标
一. P42~P43页
1.理解平移变化性质以及对应点坐标变化的规律.
学习目标
-22
4
3
1
2
x
2
1
0
9
-4
3
2
O
1
-4--4
-33
一. P50~P52页
A
B
D
C
10
8
7
6
5
4
3
2
1
一. P39~P40
第 象限
坐标符号( , )
( )
第 象限
坐标符号( , )
( )
第 象限
坐标符号( , )
( )
建立平面直角坐标系
第 象限
坐标符号(+,+)
(垂直且有公共原点)
(两条数轴)
y
x
1
C
B
A
O
二.独立完成下列作业
二.独立完成下列作业
二.独立完成下列作业
二.独立完成下列作业
二.独立完成下列作业
一. P40~P42
-1
4
-1
-2
-3
火车站
文化馆
11
