山东省夏津第六中学2016-2017学年高一上学期开学检测数学试题
文档属性
| 名称 | 山东省夏津第六中学2016-2017学年高一上学期开学检测数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-03 00:00:00 | ||
图片预览



文档简介
2016年高一新生开学检测
数学试题
(时间:120分钟,总分:120分)
2016.9
一、选择题(每小题3分,共30分)
1、人体内的某种细胞的形状可近似看作是球状,它的直径为 0.00000156m,则这个数用科学记数法表示是
(
)
A.1.56×10 6m
B.1.56×10 5m
C.156×10 5m
D.1.56×106m
2.下列各组根式中,属于同类二次根式是(
)
A.
B.
C.
D.
3.在下列四个图案中,既是轴对称图形,又是中心对称图形的是
(
)
4.下面关于x的方程中:①ax2+x+2=0;②3(x-9)2-(x+1)2=1;③x+3=;④x2-a=0(a为任意实数);
⑤=x-1.一元二次方程的个数是( )
A.1
B.2
C.3
D.4
5.从正方形铁片上截去2cm宽的一个长方形,剩余矩形的面积为80cm2,则原来正方形的面积为(
)
A.100cm2
B.121cm2
C.144cm2
D.169cm2
6.三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是(
)
A.24
B.48
C.24或8
D.8
7.
抛物线向右平移1个单位,再向下平移2个单位,所得到的抛物线是(
)
A.
B.
C.
D.
8.
⊙O的半径r=5
cm,圆心到直线l的距离OM=4
cm,在直线l上有一点P,且
PM=3
cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
9.直线与抛物线的交点个数是(
)
A.0个
B.1个
C.2个
D.互相重合的两个
10.关于抛物线(a≠0),下面几点结论中,正确的有(
)
当a0时,对称轴左边y随x的增大而减小,对称轴右边y随x的增大而增大,当a0时,情况相反.
抛物线的最高点或最低点都是指抛物线的顶点.
只要解析式的二次项系数的绝对值相同,两条抛物线的形状就相同.
一元二次方程(a≠0)的根,就是抛物线与x
轴
交点的横坐标.
A.①②③④
B.①②③
C.
①②
D.①
二、填空题(每小题4分,共20分)
1.使有意义,则x的取值范围是__________.
2、
一组数据
1,2,a
的平均数为
2,另一组数据
1,a,1,2,b
的唯一众数为
1,则数据
1,a,1,2,b
的中位数为________________
。
3.为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为10
m2
提高到12.1
m2若每年的年增长率相同且设为x,则列出的方程是
.
4.已知方程x2-7x+12=0的两根恰好是Rt△ABC的两条边的长,则Rt△ABC的第三边长为________.
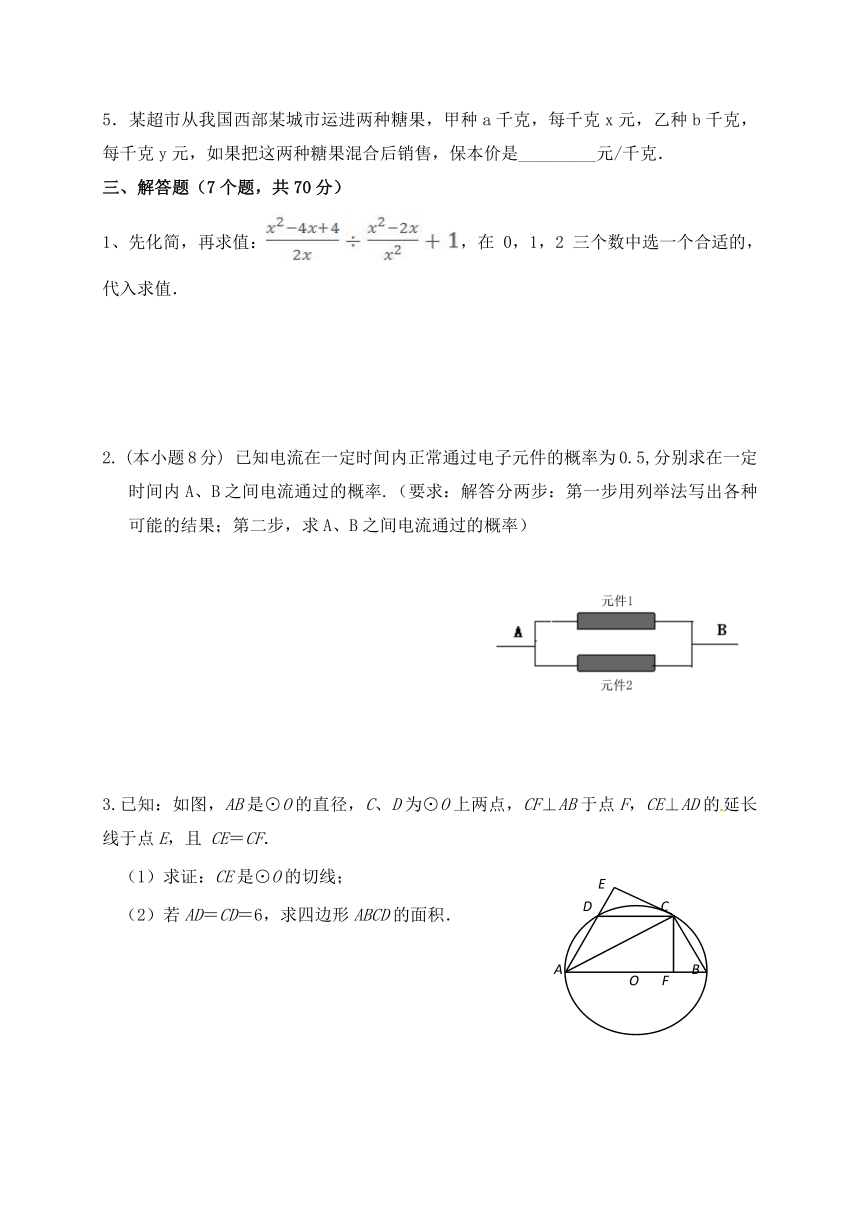
5.某超市从我国西部某城市运进两种糖果,甲种a千克,每千克x元,乙种b千克,每千克y元,如果把这两种糖果混合后销售,保本价是_________元/千克.
三、解答题(7个题,共70分)
1、先化简,再求值:,在
0,1,2
三个数中选一个合适的,代入求值.
2.
(本小题8分)
已知电流在一定时间内正常通过电子元件的概率为0.5,分别求在一定时间内A、B之间电流通过的概率.(要求:解答分两步:第一步用列举法写出各种可能的结果;第二步,求A、B之间电流通过的概率)
3.已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD的延长线于点E,且
CE=CF.
(1)求证:CE是⊙O的切线;
(2)若AD=CD=6,求四边形ABCD的面积.
4、我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”.如图 1,四边形 ABCD 即为“准等腰梯形”.其中 ∠B=∠C.
(1)在图 1 所示的“准等腰梯形” ABCD 中,选择合适的一个顶点引一条直线将四边形 ABCD 分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形(画出一种示意图即可);
(2)如图 2,在“准等腰梯形” ABCD 中,∠B=∠C,E 为边 BC 上一点,若 AB∥DE,AE∥DC.
求证:
(3)在由不平行于 BC 的直线 AD 截 △PBC 所得的四边形 ABCD 中,∠BAD 与 ∠ADC 的平分线交于点 E,若 EB=EC,请问当点 E 在四边形 ABCD 内部时(即图 3 所示情形),四边形 ABCD 是不是“准等腰梯形”,为什么?若点 E 不在四边形 ABCD 内部时,情况又将如何?写出你的结论(不必说明理由).
5.某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.
经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
6.已知:如图,二次函数y
=
ax2
+
bx
+
c的图象与x轴交于A、B两点,其中A点坐标为(
-1,0
),点C
(
0,5
),另抛物线经过点
(
1,8
),M为它的顶点.
(
1
)
求抛物线的解析式;
(
2
)
求△MCB的面积S△M
C
B.
7、(12分)如图,某公路隧道横截面为抛物线,其最大高度为 6 米,底部宽度 OM 为 12 米.
现以 O 点为原点,OM 所在直线为 x 轴建立直角坐标系.
(1)直接写出点 M 及抛物线顶点 P 的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架” AD DC CB,使 C,D 点在抛物线上,A,B 点在地面 OM 上,则这个“支撑架”总长的最大值是多少?
一.1-10.ACABACABCA
.
二.1.
2.1
3.10(1+x)2=12.1
4.5或
5.
三.1.原式=x/2
;当
x=1
时,原式=1/2.解析:当
x=0
或
2
时分式无意义.
2.
P(通电)=
3、证明:(1)连结OC.
∵CF⊥AB
,CE⊥AD,且CE=CF
∴∠CAE=∠CAB
∵
OC=OA
∴
∠CAB=∠OCA
∴∠CAE=∠OCA
∴∠OCA+∠ECA=∠CAE+∠ECA=90°
又∵OC是⊙O的半径
∴CE是⊙O的切线
(2)∵AD=CD
∴∠DAC=∠DCA=∠CAB
∴DC//AB
∵∠CAE=∠OCA
∴OC//AD
∴四边形AOCD是平行四边形
∴OC=AD=6,AB=12∵∠CAE=∠CAB
∴弧CD=弧CB
∴CD=CB=6
∴△OCB是等边三角形
∴∴S四边形ABCD=
4、(1)如图所示(画出其中一种即可).
(2)答案:
∵AE∥CD, ∴∠AEB=∠C,∵AB∥ED, ∴∠B=∠DEC, ∴△ABE∽△DEC.即 AE/CD=BE/EC.
又 ∠B=∠C, ∴△ABE 为等腰三角形,AB=AE.故 AB/CD=BE/EC.
(3)过 E 点分别作 EF⊥AB,EG⊥AD,EH⊥CD,垂足分别为 F,G,H(如图).
∵AE 平分 ∠BAD,
∴EF=EG,
又 ED 平分 ∠ADC,
∴EG=EH, ∴EF=EH,
∵EB=EC, ∴Rt△BFE Rt△CHE, ∴∠3=∠4,
∵EB=EC, ∴∠1=∠2, ∴∠1+∠3=∠2+∠4.即 ∠ABC=∠DCB.
∵ 四边形 ABCD 为 AD 截某三角形所得,且 AD 不平行 BC,
∴ 四边形 ABCD 为“准等腰梯形”.
当点 E 不在四边形 ABCD 内部时,有两种情况:
当点 E 在四边形 ABCD 的边 BC 上时,四边形 ABCD 为“准等腰梯形”;
当点 E 在四边形 ABCD 的外部时,四边形 ABCD 仍为“准等腰梯形”.
5、解:(1)设涨x元,则有(10+x)(500-20x)=6000化简得x2-15x+500=0
∴x1=5,
x2=10(舍)
(2)设利润为y,则有
y=(10+x)(500-20x)=-20(x-7.5)2+6125
当x=7.5时,y最大为6125
6、解:(1)依题意:
(2)令y=0,得(x-5)(x+1)=0,x1=5,x2=-1
∴B(5,0)
由,得M(2,9)
作ME⊥y轴于点E,
则
可得S△MCB=15.
7、(12分)(1)M(12,0),P(6,6).
(2)根据顶点 P 的坐标,可设抛物线的解析式为 y=a(x 6)2+6.
将点 O(0,0) 代入解析式求得 a= 1/6.
所以这条抛物线的解析式为:y= 1/6(x 6)2+6= 1/6x2+2x.
(3)答案:设点 A 的坐标为 (a,0),则 AD=BC= 1/6a2+2a,AB=12 2a.
设这个支架的总长为 l.根据题意,得
l=AD+BC+AB=2 ( 1/6a2+2a)+12 2a= 1/3(a 3)2+15.
则当 a=3 时,y最大=15.
所以这个"支撑架"总长的最大值是 15 米
A
B
O
F
E
D
C
数学试题
(时间:120分钟,总分:120分)
2016.9
一、选择题(每小题3分,共30分)
1、人体内的某种细胞的形状可近似看作是球状,它的直径为 0.00000156m,则这个数用科学记数法表示是
(
)
A.1.56×10 6m
B.1.56×10 5m
C.156×10 5m
D.1.56×106m
2.下列各组根式中,属于同类二次根式是(
)
A.
B.
C.
D.
3.在下列四个图案中,既是轴对称图形,又是中心对称图形的是
(
)
4.下面关于x的方程中:①ax2+x+2=0;②3(x-9)2-(x+1)2=1;③x+3=;④x2-a=0(a为任意实数);
⑤=x-1.一元二次方程的个数是( )
A.1
B.2
C.3
D.4
5.从正方形铁片上截去2cm宽的一个长方形,剩余矩形的面积为80cm2,则原来正方形的面积为(
)
A.100cm2
B.121cm2
C.144cm2
D.169cm2
6.三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是(
)
A.24
B.48
C.24或8
D.8
7.
抛物线向右平移1个单位,再向下平移2个单位,所得到的抛物线是(
)
A.
B.
C.
D.
8.
⊙O的半径r=5
cm,圆心到直线l的距离OM=4
cm,在直线l上有一点P,且
PM=3
cm,则点P( )
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.可能在⊙O上或在⊙O内
9.直线与抛物线的交点个数是(
)
A.0个
B.1个
C.2个
D.互相重合的两个
10.关于抛物线(a≠0),下面几点结论中,正确的有(
)
当a0时,对称轴左边y随x的增大而减小,对称轴右边y随x的增大而增大,当a0时,情况相反.
抛物线的最高点或最低点都是指抛物线的顶点.
只要解析式的二次项系数的绝对值相同,两条抛物线的形状就相同.
一元二次方程(a≠0)的根,就是抛物线与x
轴
交点的横坐标.
A.①②③④
B.①②③
C.
①②
D.①
二、填空题(每小题4分,共20分)
1.使有意义,则x的取值范围是__________.
2、
一组数据
1,2,a
的平均数为
2,另一组数据
1,a,1,2,b
的唯一众数为
1,则数据
1,a,1,2,b
的中位数为________________
。
3.为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为10
m2
提高到12.1
m2若每年的年增长率相同且设为x,则列出的方程是
.
4.已知方程x2-7x+12=0的两根恰好是Rt△ABC的两条边的长,则Rt△ABC的第三边长为________.
5.某超市从我国西部某城市运进两种糖果,甲种a千克,每千克x元,乙种b千克,每千克y元,如果把这两种糖果混合后销售,保本价是_________元/千克.
三、解答题(7个题,共70分)
1、先化简,再求值:,在
0,1,2
三个数中选一个合适的,代入求值.
2.
(本小题8分)
已知电流在一定时间内正常通过电子元件的概率为0.5,分别求在一定时间内A、B之间电流通过的概率.(要求:解答分两步:第一步用列举法写出各种可能的结果;第二步,求A、B之间电流通过的概率)
3.已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD的延长线于点E,且
CE=CF.
(1)求证:CE是⊙O的切线;
(2)若AD=CD=6,求四边形ABCD的面积.
4、我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”.如图 1,四边形 ABCD 即为“准等腰梯形”.其中 ∠B=∠C.
(1)在图 1 所示的“准等腰梯形” ABCD 中,选择合适的一个顶点引一条直线将四边形 ABCD 分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形(画出一种示意图即可);
(2)如图 2,在“准等腰梯形” ABCD 中,∠B=∠C,E 为边 BC 上一点,若 AB∥DE,AE∥DC.
求证:
(3)在由不平行于 BC 的直线 AD 截 △PBC 所得的四边形 ABCD 中,∠BAD 与 ∠ADC 的平分线交于点 E,若 EB=EC,请问当点 E 在四边形 ABCD 内部时(即图 3 所示情形),四边形 ABCD 是不是“准等腰梯形”,为什么?若点 E 不在四边形 ABCD 内部时,情况又将如何?写出你的结论(不必说明理由).
5.某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.
经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
6.已知:如图,二次函数y
=
ax2
+
bx
+
c的图象与x轴交于A、B两点,其中A点坐标为(
-1,0
),点C
(
0,5
),另抛物线经过点
(
1,8
),M为它的顶点.
(
1
)
求抛物线的解析式;
(
2
)
求△MCB的面积S△M
C
B.
7、(12分)如图,某公路隧道横截面为抛物线,其最大高度为 6 米,底部宽度 OM 为 12 米.
现以 O 点为原点,OM 所在直线为 x 轴建立直角坐标系.
(1)直接写出点 M 及抛物线顶点 P 的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架” AD DC CB,使 C,D 点在抛物线上,A,B 点在地面 OM 上,则这个“支撑架”总长的最大值是多少?
一.1-10.ACABACABCA
.
二.1.
2.1
3.10(1+x)2=12.1
4.5或
5.
三.1.原式=x/2
;当
x=1
时,原式=1/2.解析:当
x=0
或
2
时分式无意义.
2.
P(通电)=
3、证明:(1)连结OC.
∵CF⊥AB
,CE⊥AD,且CE=CF
∴∠CAE=∠CAB
∵
OC=OA
∴
∠CAB=∠OCA
∴∠CAE=∠OCA
∴∠OCA+∠ECA=∠CAE+∠ECA=90°
又∵OC是⊙O的半径
∴CE是⊙O的切线
(2)∵AD=CD
∴∠DAC=∠DCA=∠CAB
∴DC//AB
∵∠CAE=∠OCA
∴OC//AD
∴四边形AOCD是平行四边形
∴OC=AD=6,AB=12∵∠CAE=∠CAB
∴弧CD=弧CB
∴CD=CB=6
∴△OCB是等边三角形
∴∴S四边形ABCD=
4、(1)如图所示(画出其中一种即可).
(2)答案:
∵AE∥CD, ∴∠AEB=∠C,∵AB∥ED, ∴∠B=∠DEC, ∴△ABE∽△DEC.即 AE/CD=BE/EC.
又 ∠B=∠C, ∴△ABE 为等腰三角形,AB=AE.故 AB/CD=BE/EC.
(3)过 E 点分别作 EF⊥AB,EG⊥AD,EH⊥CD,垂足分别为 F,G,H(如图).
∵AE 平分 ∠BAD,
∴EF=EG,
又 ED 平分 ∠ADC,
∴EG=EH, ∴EF=EH,
∵EB=EC, ∴Rt△BFE Rt△CHE, ∴∠3=∠4,
∵EB=EC, ∴∠1=∠2, ∴∠1+∠3=∠2+∠4.即 ∠ABC=∠DCB.
∵ 四边形 ABCD 为 AD 截某三角形所得,且 AD 不平行 BC,
∴ 四边形 ABCD 为“准等腰梯形”.
当点 E 不在四边形 ABCD 内部时,有两种情况:
当点 E 在四边形 ABCD 的边 BC 上时,四边形 ABCD 为“准等腰梯形”;
当点 E 在四边形 ABCD 的外部时,四边形 ABCD 仍为“准等腰梯形”.
5、解:(1)设涨x元,则有(10+x)(500-20x)=6000化简得x2-15x+500=0
∴x1=5,
x2=10(舍)
(2)设利润为y,则有
y=(10+x)(500-20x)=-20(x-7.5)2+6125
当x=7.5时,y最大为6125
6、解:(1)依题意:
(2)令y=0,得(x-5)(x+1)=0,x1=5,x2=-1
∴B(5,0)
由,得M(2,9)
作ME⊥y轴于点E,
则
可得S△MCB=15.
7、(12分)(1)M(12,0),P(6,6).
(2)根据顶点 P 的坐标,可设抛物线的解析式为 y=a(x 6)2+6.
将点 O(0,0) 代入解析式求得 a= 1/6.
所以这条抛物线的解析式为:y= 1/6(x 6)2+6= 1/6x2+2x.
(3)答案:设点 A 的坐标为 (a,0),则 AD=BC= 1/6a2+2a,AB=12 2a.
设这个支架的总长为 l.根据题意,得
l=AD+BC+AB=2 ( 1/6a2+2a)+12 2a= 1/3(a 3)2+15.
则当 a=3 时,y最大=15.
所以这个"支撑架"总长的最大值是 15 米
A
B
O
F
E
D
C
同课章节目录
