新人教版勾股定理第一课时课件
文档属性
| 名称 | 新人教版勾股定理第一课时课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-25 00:00:00 | ||
图片预览




文档简介
课件24张PPT。 18.1勾股定理实验中学
王庆伟教学目标知识目标:掌握勾股定理的内容,了解勾股定理的证明,会用它进行有关的计算。
能力目标:通过学生动手、动脑、动口,培养学生交往协作能力、组织能力、实践能力和创造能力。
德育目标:
通过对比介绍中国古代和西方数学家对勾股定理的证明,使学生了解不同文化背景下数学思维方法的差异,同时进行爱国主义教育。
重点:探索和证明勾股定理
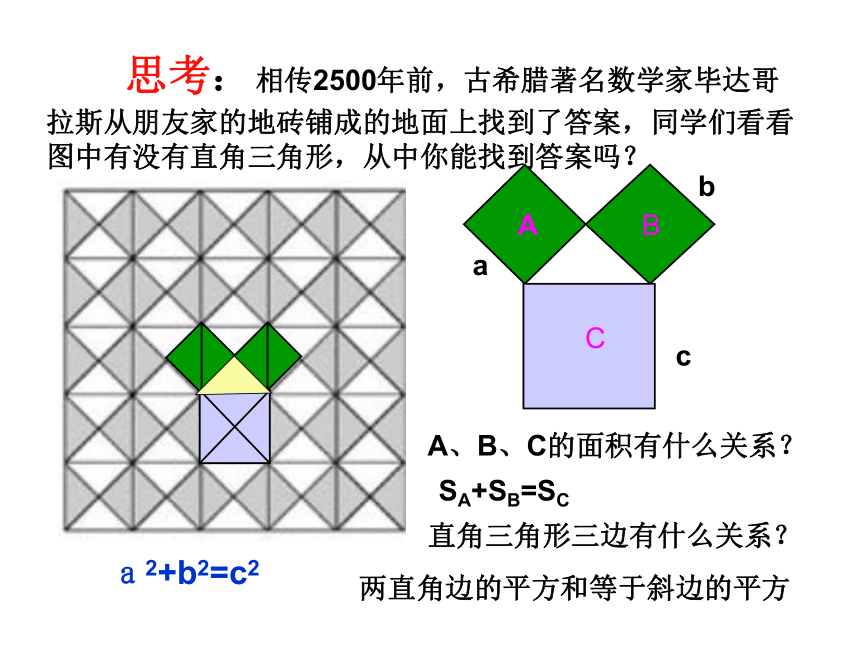
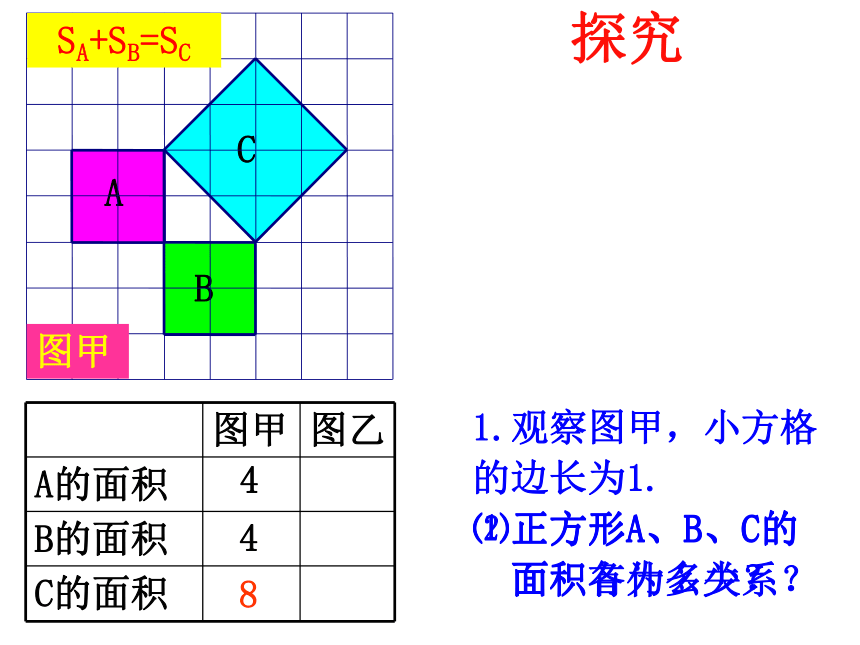
难点:理解勾股定理的推导过程 这就是本届大会会徽的图案.活动 1你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。 思考: 相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方a2+b2=c2abc448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
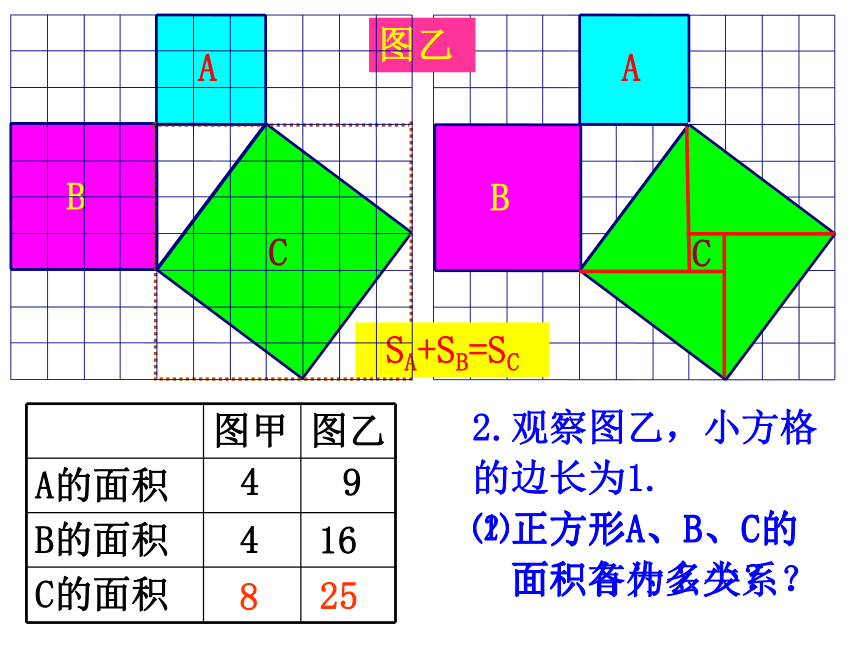
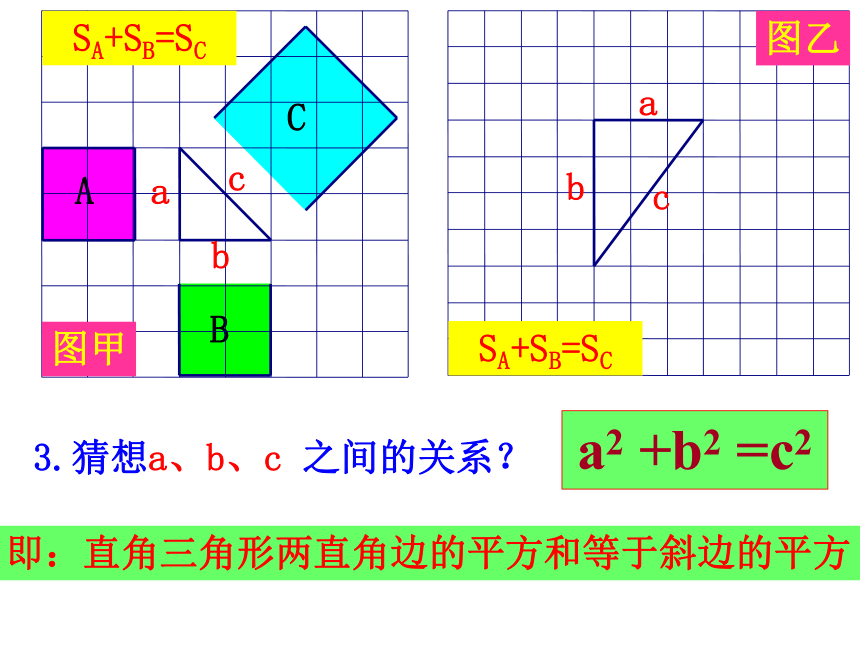
面积有什么关系?探究C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625⑵正方形A、B、C的
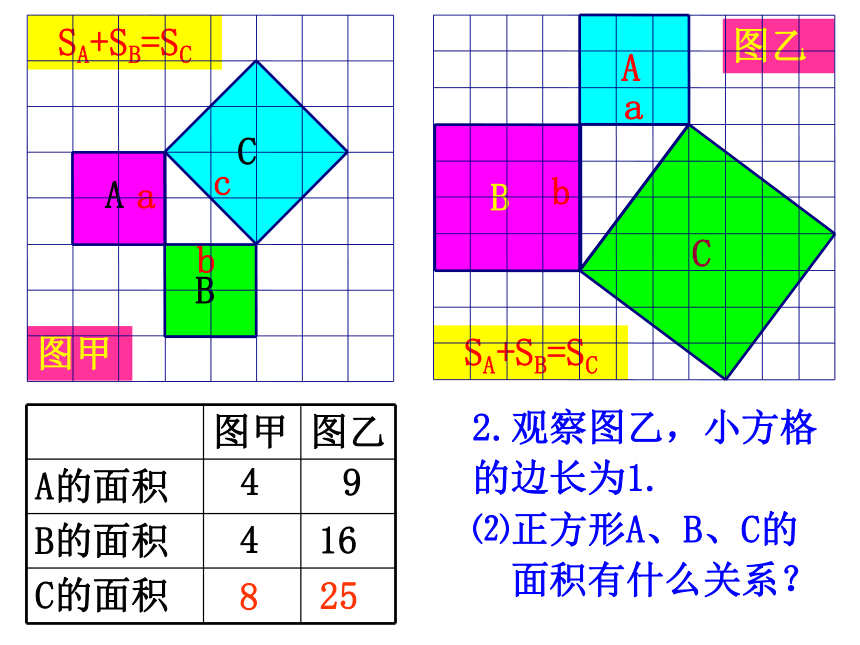
面积有什么关系?448SA+SB=SC图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图甲abcabc3.猜想a、b、c 之间的关系?a2 +b2 =c2即:直角三角形两直角边的平方和等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。abc你能证明这个命题是正确的命题吗?如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
试一试(合作探究) ccc(a-b)2(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2对比两种方法,
你能得到什么? 定理:经过证明被确认为正确的命题叫做定理。 这种证法是美国第二十任总统伽菲尔德发现的,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦结论变形c2 = a2 + b2练习:
1、求下列图中字母所表示的正方形的面积=625=1442、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 0实际应用1.如图,这了测得湖两岸点A和点C间的距离,一个观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200m,BC=160m,根据测量结果求点A,C间的距离.ACB120m200m160m 2.借助勾股定理,利用升旗的绳子和卷尺,请你设计一个方案,测算出旗杆的高度,小结:说说这节课你有什么收获?再见
王庆伟教学目标知识目标:掌握勾股定理的内容,了解勾股定理的证明,会用它进行有关的计算。
能力目标:通过学生动手、动脑、动口,培养学生交往协作能力、组织能力、实践能力和创造能力。
德育目标:
通过对比介绍中国古代和西方数学家对勾股定理的证明,使学生了解不同文化背景下数学思维方法的差异,同时进行爱国主义教育。
重点:探索和证明勾股定理
难点:理解勾股定理的推导过程 这就是本届大会会徽的图案.活动 1你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。 思考: 相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方a2+b2=c2abc448SA+SB=SCC图甲1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?⑵正方形A、B、C的
面积有什么关系?探究C图乙2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?91625⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图乙2.观察图乙,小方格
的边长为1.91625SA+SB=SC⑵正方形A、B、C的
面积有什么关系?448SA+SB=SC图甲abcabc3.猜想a、b、c 之间的关系?a2 +b2 =c2即:直角三角形两直角边的平方和等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。abc你能证明这个命题是正确的命题吗?如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
试一试(合作探究) ccc(a-b)2(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2对比两种方法,
你能得到什么? 定理:经过证明被确认为正确的命题叫做定理。 这种证法是美国第二十任总统伽菲尔德发现的,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦结论变形c2 = a2 + b2练习:
1、求下列图中字母所表示的正方形的面积=625=1442、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 0实际应用1.如图,这了测得湖两岸点A和点C间的距离,一个观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200m,BC=160m,根据测量结果求点A,C间的距离.ACB120m200m160m 2.借助勾股定理,利用升旗的绳子和卷尺,请你设计一个方案,测算出旗杆的高度,小结:说说这节课你有什么收获?再见
