2016-2017学年上学期苏科版八年级上册数学第一章《全等三角形》单元检测
文档属性
| 名称 | 2016-2017学年上学期苏科版八年级上册数学第一章《全等三角形》单元检测 |  | |
| 格式 | zip | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-03 21:30:26 | ||
图片预览


文档简介
第一章《全等三角形》单元检测
(满分:100分
时间:90分钟)
一、选择题
(每题2分,共20分)
1.下列说法错误的是
(
)
A.全等三角形的对应边相等
B.全等三角形的角相等
C.全等三角形的周长相等
D.全等三角形的面积相等
2.已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DE的长为
(
)
A.4
B.5
C.6
D.不能确定
3.已知△ABC的六个元素,下面甲、乙、丙三个三角形中和△ABC全等的图形是
(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
4.在如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为
(
)
A.330°
B.315°
C.310°
D.320°
5.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P的个数为
(
)
A.1
B.2
C.3
D.4
6.四个角分别相等且四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A'B'C'D'中,AB=A'B',BC=B'C',CD=C'D'.要使四边形ABCD≌四边形A'B'C'D',可以添加的条件是
(
)
A.DA=D'A'
B.∠B=∠B'
C.∠B=∠B',∠C=∠C'
D.∠B=∠B',∠D=∠D'
7.如图,在△ABC中,AQ=PQ,PR=PS,若PR⊥AB,PS⊥AC,垂足分别为点R,S,给出下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS.其中正确的是
(
)
A.①②③
B.①
C.①②
D.①③
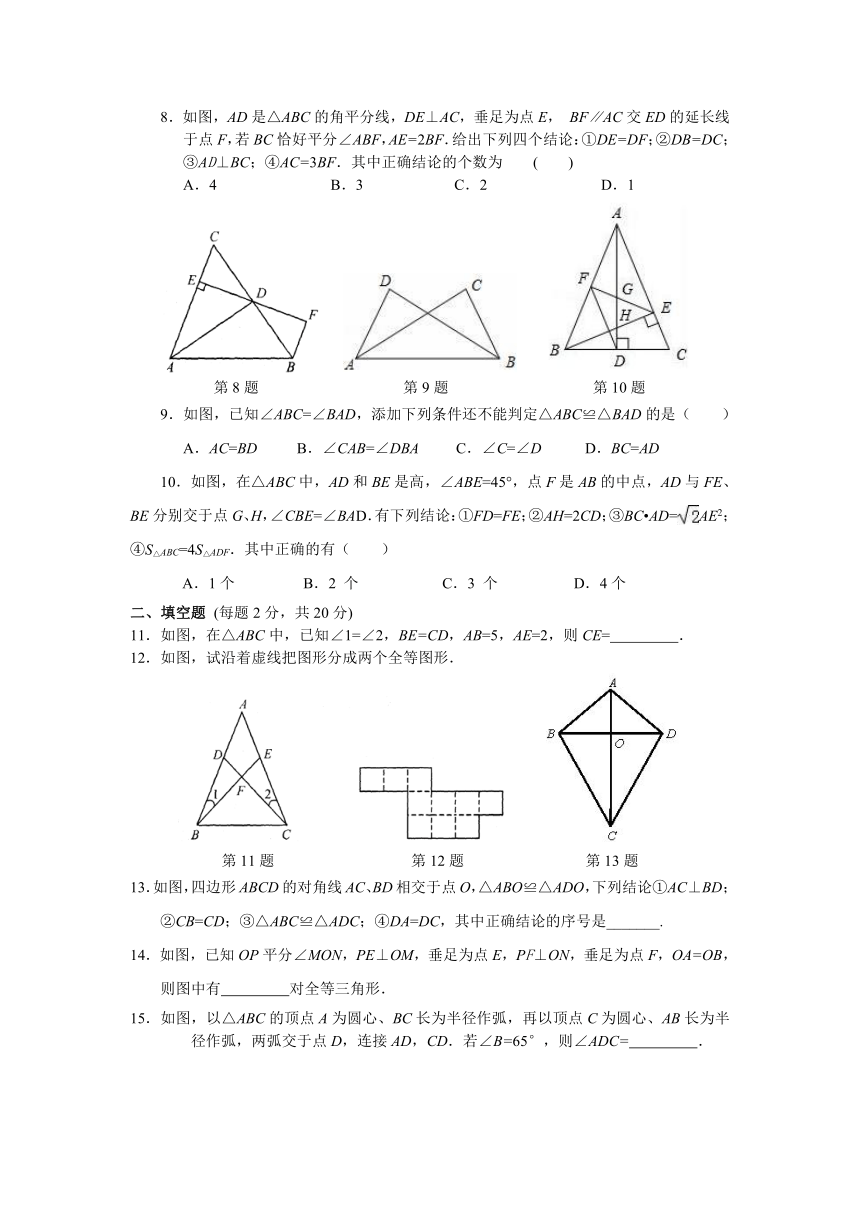
8.如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,
BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确结论的个数为
(
)
A.4
B.3
C.2
D.1
第8题
第9题
第10题
9.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.BC=AD
10.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC AD=AE2;④S△ABC=4S△ADF.其中正确的有( )
A.1个
B.2
个
C.3
个
D.4个
二、填空题
(每题2分,共20分)
11.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=
.
12.如图,试沿着虚线把图形分成两个全等图形.
第11题
第12题
第13题
13.如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中正确结论的序号是_______.
14.如图,已知OP平分∠MON,PE⊥OM,垂足为点E,PF⊥ON,垂足为点F,OA=OB,则图中有
对全等三角形.
15.如图,以△ABC的顶点A为圆心、BC长为半径作弧,再以顶点C为圆心、AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC=
.
第14题
第15题
第17题
16.在△ADB和△ADC中,给出下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.其中能得出△ADB≌△ADC的序号是
.
17.如图,黄芳不小心把一块三角形的玻璃摔成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第
块去配,其依据是定理
(可以用字母简写).
18.如图,AB∥CF,E为DF的中点,若AB=7
cm,CF=4cm,则BD=
cm.
19.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,则∠ABC=
.
第18题
第19题
第20题
20.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC≌△QPA.
三、解答题
(共60分)
21.(本题6分)
如图,点C,D在AB上,且AC=BD,AE=FB,DE=FC.求证:
(1)
△ADE≌△BCF;
(2)
AE∥BF.
22.(本题5分)
如图,AB=AC,BD=CD,DE⊥AB,垂足为点E,DF⊥AC,垂足为点F.求证:DE=DF.
23.(本题5分)
如图,已知点B,C,D,E在同一条直线上,AB=FC,AD=FE,BC=DE,探索AB与FC的位置关系,并说明理由.
24.(本题6分)
有两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,
阴影部分为重叠部分,点O为边AC和DF的交点.
(1)
不重叠的两部分△AOF与△DOC是否全等
为什么
(2)
连接BO,求证:BO平分∠ABD.
25.(本题6分)
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:DE=AD+BE.
26.(本题8分)
如图,把一个Rt△ACB(∠ACB=90°)绕着顶点B按顺时针方向旋转60°,使得点C旋转到边AB上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)
求证:CF=DG;
(2)
求∠FHG的度数.
27.(本题8分)
如图,在△ABC中,∠ACB=90°,AC=BC,AE是边BC上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)
求证:AE=CD;
(2)
若AC=12
cm,求BD的长.
28.(本题8分)
如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,此人的运动速度为1
m/s,求这个人运动了多长时间.
29.(本题10分)
CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)
若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的结论仍然成立,并说明理由.
(2)
如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段间数量关系的合理猜想:
.
参考答案
一、选择题
1.B
2.A
3.D
4.B
5.B
6.C
7.C
8.A
(提示:∵
BC恰好平分∠ABF,∴
∠ABD=∠DBF,又∵
BF∥AC,∴
∠C=∠DBF,∴
∠C=∠ABD,∴AB=AC.∵
AD是△ABC的角平分线,∴
AD⊥BC,DB=DC.
在△DCE和△DBF中,DB=DC,∠DCE=∠DBF,∠CDE=∠BDF,∴
ADC≌△DBF,∴
DE=DF,CE=BF.又∵
AE=2BF,∴
AE=2CE,AC=AE+CE=3CE=3BF,故①②③④均为正确结论)
9.A
10.D
二、填空题
11.3
12.
13.①②③
14.3
15.65°
16.①②④
17.③
ASA
18.3
19.45°
20.5
(提示:△ABC≌△QPA时,AP=BC=5)
三、解答题
21.(1)
∵
AC=BD,∴
AC+CD=BD+CD,∴
AD=BC.在△ADE和△BCF中,AE=BF,AD=BC,DE=FC,∴
△ADE≌△BCF
(2)
∵
△ADE≌△BCF,∴
∠A=∠B,
∴
AE∥BF
22.连接AD.在△ABD
和△ACD中,AB=AC,BD=CD,AD=AD,∴
△ABD≌△ACD,∴
S△ABD=S△ACD.∵
DE⊥AB,DF⊥AC,S△ABD=×AB×DE,S△ACD=×AC×DF,
∴
DE=DF
23.AB于FC的位置关系是:AB∥FC.
理由:∵
BC=DE,∴
BC+CD=DE+CD,即BD=CE.在△ABD和△FCE中,
∴
△ABD≌△FCE,∴
∠B=∠FCE,∴
AB∥FC
24.(1)
不重叠的两部分△AOF与△DOC全等,理由如下:∵
三角形纸板ABC和DEF完全相同,∴
AB=DB,BF=BC,∴
AB-BF=DB-BC,∴
AF=DC.
在△AOF和△DOC中,∠A=∠D,∠AOF=∠DOC,AF=DC,∴
△AOF≌△DOC
(2)
连接OB.
∵
△AOF≌DOC,∴
FO=CO.
在△BFO和△BCO中,BF=BC,FO=CO,BO=BO,∴
△BFO≌△BCO,∴
∠FBO=∠CBO,即BO平分∠ABD
25.∵
∠ACB=90°,AC=BC,∴
∠ACD+∠BCE=90°.
又∵
AD⊥MN,BE⊥MN,∴
∠ADC=∠CEB=90°,∠ACD+∠DAC=90°,∴
∠BCE=∠CAD.
在△ADC和△CEB中,
∵
∠BCE=∠CAD,∠ADC=∠CEB,AC=BC,∴
△ADC≌△CEB,∴
AD=CE,DC=EB.
又∵
DE=DC+CE,∴
DE=AD+BE
26.(1)
∵
在△CBF和△DBG中,BC=BD,∠CBF=∠DBG=60°,BF=BG,∴
△CBF≌△DBG,∴
CF=DG
(2)
∵
△CBF≌△DBG,∴
∠BCF=∠BDG.又∵
∠CFB=∠DFH,∴
∠DHF=∠CBF=
60°,∴
∠FHG=180°-∠DHF=180°-60°=120°
27.(1)
∵
DB⊥BC,CF⊥AE,∴
∠DCB+∠D=∠DCB+∠AEC=90°,∴
∠D=∠AEC.又∵
∠DBC=∠ECA=90°,且BC=CA,∴
△DBC≌△ECA,∴
AE=CD
(2)由(1)知BD=EC=AC,∵
AC=12cm,∴
BD=6cm
28.∵
∠CMD=90°,∴
∠CMA+∠DMB=90°.又∵
∠CAM=90°,∴
∠CMA+∠ACM=
90°,∴
∠ACM=∠DMB.又∵
CM=MD,∴
Rt△ACM≌Rt△BMD,∴
AC=BM=3,∴
他到达点M时,运动时间为3÷1=3(s).这人运动了3s
29.(1)
=
∠α+∠BCA=180°
证明:∵
∠BEC+∠BCA=180°,∠BEC+∠BEF=180°,
∴
∠BCA=∠BEF.∵
∠BCA=∠BCE+∠ACF,∠BEF=∠BCE+∠CBE,∴
∠CBE=∠ACF.在△BCE和△CAF中,∵
∠CBE=∠ACF,∠BEC=∠CFA,CA=CB,∴
△BCE≌△CAF.∴
BE=CF
(2)EF=BE+AF
(满分:100分
时间:90分钟)
一、选择题
(每题2分,共20分)
1.下列说法错误的是
(
)
A.全等三角形的对应边相等
B.全等三角形的角相等
C.全等三角形的周长相等
D.全等三角形的面积相等
2.已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DE的长为
(
)
A.4
B.5
C.6
D.不能确定
3.已知△ABC的六个元素,下面甲、乙、丙三个三角形中和△ABC全等的图形是
(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
4.在如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为
(
)
A.330°
B.315°
C.310°
D.320°
5.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P的个数为
(
)
A.1
B.2
C.3
D.4
6.四个角分别相等且四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A'B'C'D'中,AB=A'B',BC=B'C',CD=C'D'.要使四边形ABCD≌四边形A'B'C'D',可以添加的条件是
(
)
A.DA=D'A'
B.∠B=∠B'
C.∠B=∠B',∠C=∠C'
D.∠B=∠B',∠D=∠D'
7.如图,在△ABC中,AQ=PQ,PR=PS,若PR⊥AB,PS⊥AC,垂足分别为点R,S,给出下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS.其中正确的是
(
)
A.①②③
B.①
C.①②
D.①③
8.如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,
BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确结论的个数为
(
)
A.4
B.3
C.2
D.1
第8题
第9题
第10题
9.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.BC=AD
10.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC AD=AE2;④S△ABC=4S△ADF.其中正确的有( )
A.1个
B.2
个
C.3
个
D.4个
二、填空题
(每题2分,共20分)
11.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=
.
12.如图,试沿着虚线把图形分成两个全等图形.
第11题
第12题
第13题
13.如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC,其中正确结论的序号是_______.
14.如图,已知OP平分∠MON,PE⊥OM,垂足为点E,PF⊥ON,垂足为点F,OA=OB,则图中有
对全等三角形.
15.如图,以△ABC的顶点A为圆心、BC长为半径作弧,再以顶点C为圆心、AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠ADC=
.
第14题
第15题
第17题
16.在△ADB和△ADC中,给出下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.其中能得出△ADB≌△ADC的序号是
.
17.如图,黄芳不小心把一块三角形的玻璃摔成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第
块去配,其依据是定理
(可以用字母简写).
18.如图,AB∥CF,E为DF的中点,若AB=7
cm,CF=4cm,则BD=
cm.
19.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,则∠ABC=
.
第18题
第19题
第20题
20.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC≌△QPA.
三、解答题
(共60分)
21.(本题6分)
如图,点C,D在AB上,且AC=BD,AE=FB,DE=FC.求证:
(1)
△ADE≌△BCF;
(2)
AE∥BF.
22.(本题5分)
如图,AB=AC,BD=CD,DE⊥AB,垂足为点E,DF⊥AC,垂足为点F.求证:DE=DF.
23.(本题5分)
如图,已知点B,C,D,E在同一条直线上,AB=FC,AD=FE,BC=DE,探索AB与FC的位置关系,并说明理由.
24.(本题6分)
有两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,
阴影部分为重叠部分,点O为边AC和DF的交点.
(1)
不重叠的两部分△AOF与△DOC是否全等
为什么
(2)
连接BO,求证:BO平分∠ABD.
25.(本题6分)
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为点D,E.求证:DE=AD+BE.
26.(本题8分)
如图,把一个Rt△ACB(∠ACB=90°)绕着顶点B按顺时针方向旋转60°,使得点C旋转到边AB上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)
求证:CF=DG;
(2)
求∠FHG的度数.
27.(本题8分)
如图,在△ABC中,∠ACB=90°,AC=BC,AE是边BC上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D.
(1)
求证:AE=CD;
(2)
若AC=12
cm,求BD的长.
28.(本题8分)
如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,此人的运动速度为1
m/s,求这个人运动了多长时间.
29.(本题10分)
CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)
若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的结论仍然成立,并说明理由.
(2)
如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段间数量关系的合理猜想:
.
参考答案
一、选择题
1.B
2.A
3.D
4.B
5.B
6.C
7.C
8.A
(提示:∵
BC恰好平分∠ABF,∴
∠ABD=∠DBF,又∵
BF∥AC,∴
∠C=∠DBF,∴
∠C=∠ABD,∴AB=AC.∵
AD是△ABC的角平分线,∴
AD⊥BC,DB=DC.
在△DCE和△DBF中,DB=DC,∠DCE=∠DBF,∠CDE=∠BDF,∴
ADC≌△DBF,∴
DE=DF,CE=BF.又∵
AE=2BF,∴
AE=2CE,AC=AE+CE=3CE=3BF,故①②③④均为正确结论)
9.A
10.D
二、填空题
11.3
12.
13.①②③
14.3
15.65°
16.①②④
17.③
ASA
18.3
19.45°
20.5
(提示:△ABC≌△QPA时,AP=BC=5)
三、解答题
21.(1)
∵
AC=BD,∴
AC+CD=BD+CD,∴
AD=BC.在△ADE和△BCF中,AE=BF,AD=BC,DE=FC,∴
△ADE≌△BCF
(2)
∵
△ADE≌△BCF,∴
∠A=∠B,
∴
AE∥BF
22.连接AD.在△ABD
和△ACD中,AB=AC,BD=CD,AD=AD,∴
△ABD≌△ACD,∴
S△ABD=S△ACD.∵
DE⊥AB,DF⊥AC,S△ABD=×AB×DE,S△ACD=×AC×DF,
∴
DE=DF
23.AB于FC的位置关系是:AB∥FC.
理由:∵
BC=DE,∴
BC+CD=DE+CD,即BD=CE.在△ABD和△FCE中,
∴
△ABD≌△FCE,∴
∠B=∠FCE,∴
AB∥FC
24.(1)
不重叠的两部分△AOF与△DOC全等,理由如下:∵
三角形纸板ABC和DEF完全相同,∴
AB=DB,BF=BC,∴
AB-BF=DB-BC,∴
AF=DC.
在△AOF和△DOC中,∠A=∠D,∠AOF=∠DOC,AF=DC,∴
△AOF≌△DOC
(2)
连接OB.
∵
△AOF≌DOC,∴
FO=CO.
在△BFO和△BCO中,BF=BC,FO=CO,BO=BO,∴
△BFO≌△BCO,∴
∠FBO=∠CBO,即BO平分∠ABD
25.∵
∠ACB=90°,AC=BC,∴
∠ACD+∠BCE=90°.
又∵
AD⊥MN,BE⊥MN,∴
∠ADC=∠CEB=90°,∠ACD+∠DAC=90°,∴
∠BCE=∠CAD.
在△ADC和△CEB中,
∵
∠BCE=∠CAD,∠ADC=∠CEB,AC=BC,∴
△ADC≌△CEB,∴
AD=CE,DC=EB.
又∵
DE=DC+CE,∴
DE=AD+BE
26.(1)
∵
在△CBF和△DBG中,BC=BD,∠CBF=∠DBG=60°,BF=BG,∴
△CBF≌△DBG,∴
CF=DG
(2)
∵
△CBF≌△DBG,∴
∠BCF=∠BDG.又∵
∠CFB=∠DFH,∴
∠DHF=∠CBF=
60°,∴
∠FHG=180°-∠DHF=180°-60°=120°
27.(1)
∵
DB⊥BC,CF⊥AE,∴
∠DCB+∠D=∠DCB+∠AEC=90°,∴
∠D=∠AEC.又∵
∠DBC=∠ECA=90°,且BC=CA,∴
△DBC≌△ECA,∴
AE=CD
(2)由(1)知BD=EC=AC,∵
AC=12cm,∴
BD=6cm
28.∵
∠CMD=90°,∴
∠CMA+∠DMB=90°.又∵
∠CAM=90°,∴
∠CMA+∠ACM=
90°,∴
∠ACM=∠DMB.又∵
CM=MD,∴
Rt△ACM≌Rt△BMD,∴
AC=BM=3,∴
他到达点M时,运动时间为3÷1=3(s).这人运动了3s
29.(1)
=
∠α+∠BCA=180°
证明:∵
∠BEC+∠BCA=180°,∠BEC+∠BEF=180°,
∴
∠BCA=∠BEF.∵
∠BCA=∠BCE+∠ACF,∠BEF=∠BCE+∠CBE,∴
∠CBE=∠ACF.在△BCE和△CAF中,∵
∠CBE=∠ACF,∠BEC=∠CFA,CA=CB,∴
△BCE≌△CAF.∴
BE=CF
(2)EF=BE+AF
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
