第六章一次函数单元测试卷(含解析)
图片预览


文档简介
〖鲁教版五四制七年级上数学单元测试卷〗
第六章《一次函数》
班级: 姓名: 得分:
(时间90分钟 满分100分)
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
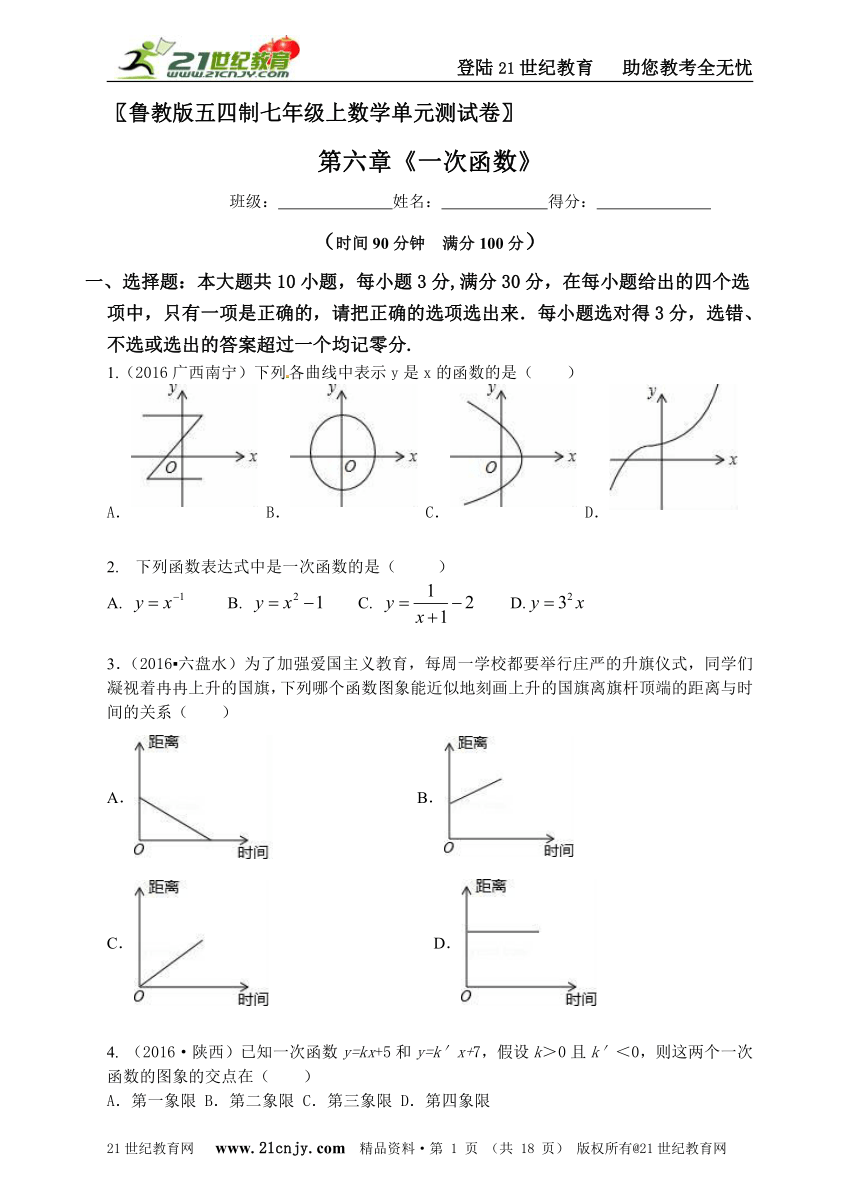
1.(2016广西南宁)下列各曲线中表示y是x的函数的是( )
A. B. C. D.
2. 下列函数表达式中是一次函数的是( )
A. B. C. D.
3.(2016?六盘水)为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列哪个函数图象能近似地刻画上升的国旗离旗杆顶端的距离与时间的关系( )
A. B.
C. D.
4. (2016·陕西)已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 直线上有两点,点A(—2,),点B(3,),则和的大小关系( )
A. B. C. D.无法判定
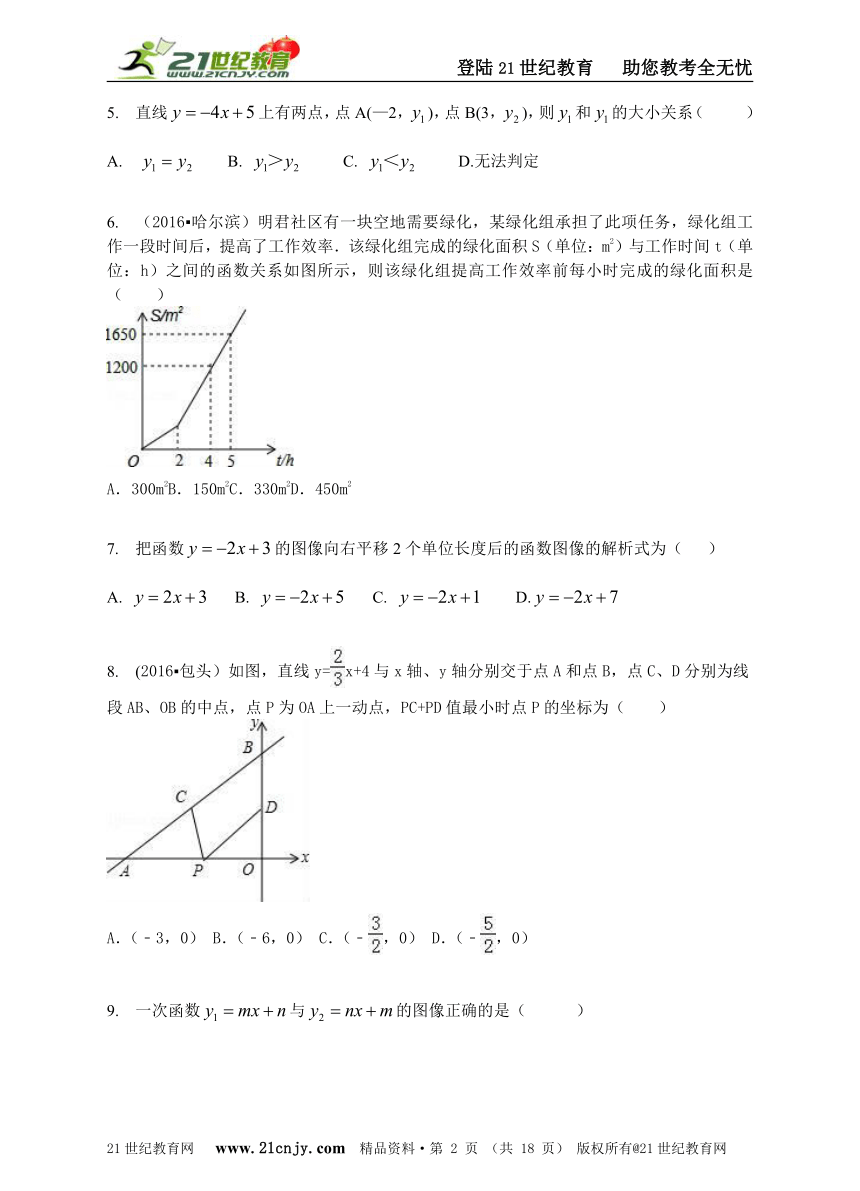
6. (2016?哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300m2B.150m2C.330m2D.450m2
7. 把函数的图像向右平移2个单位长度后的函数图像的解析式为( )
A. B. C. D.
8. (2016?包头)如图,直线y=x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0) B.(﹣6,0) C.(﹣,0) D.(﹣,0)
一次函数与的图像正确的是( )
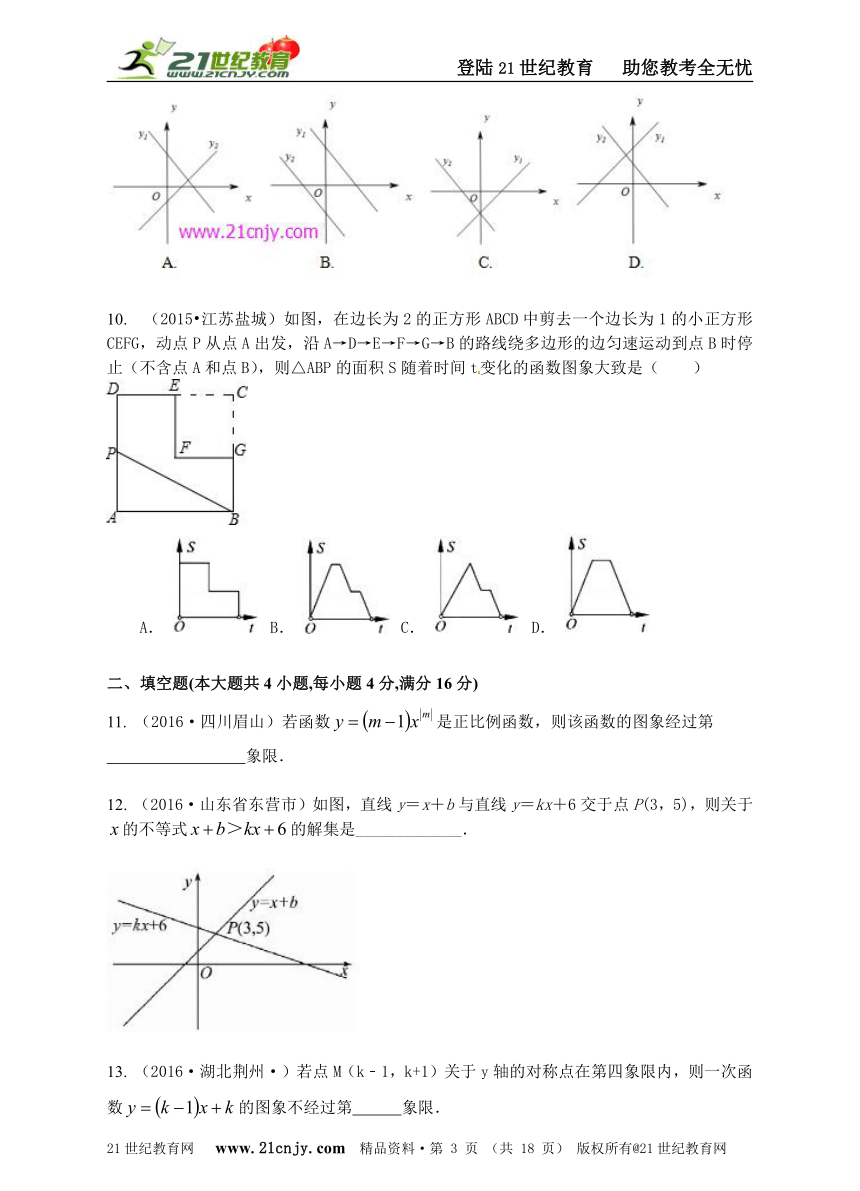
10. (2015?江苏盐城)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分)
11. (2016·四川眉山)若函数是正比例函数,则该函数的图象经过第
象限.
12. (2016·山东省东营市)如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于的不等式的解集是_____________.
13. (2016·湖北荆州·)若点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数的图象不经过第 象限.
14. (2016?山东德州)如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线,,过点(1,0)作x轴的垂线交于点,过点作y轴的垂线交于点,过点作x轴的垂线交于点,过点作y轴的垂线交于点,…依次进行下去,则点的坐标为 .
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)
15. (本题满分6分)
(2016?北京)已知y是 的函数,自变量x的取值范围是> 0,下表是y与的几组对应值.
x
···
1
2
3
5
7
9
···
y
···
1.98
3.95
2.63
1.58
1.13
0.88
···
小腾根据学习函数的经验,利用上述表格所反映出的y与之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
根据画出的函数图象,写出:
x=4对应的函数值y约为____;
该函数的一条性质:_______________.
16. (本题满分6分)
(2016?山东滨州)星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
17. (本题满分9分)
(2016?上海)某物流公司引进、两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,种机器人于某日0时开始搬运,过了1小时,种机器人也开始搬运,如图,线段表示种机器人的搬运量(千克)与时间(时)的函数图像,线段表示种机器人的搬运量(千克)与(时)的函数图像,根据图像提供的信息,解答下列问题:
(1)求关于的函数解析式;
(2)如果、两种机器人各连续搬运5个小时,那么种机器人比种机器人多搬运了多少千克?
18. (本题满分9分)
(2015·湖北省潜江市、天门市、仙桃市、江汉油田)随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
7
25
0.01
B
m
n
0.01
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
19. (本题满分12分)
(2016?长春)甲、乙两车分别从A、B两地同时出发.甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
(1)求甲车从A地到达B地的行驶时间.
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求乙车到达A地时甲车距A地的路程.
20. (本题满分12分)
(2016?齐齐哈尔)有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.
〖鲁教版五四制七年级上数学单元测试卷〗
第六章《一次函数》答案与解析
3.【答案】:A
【解析】:考点 函数的图象.
分析 设旗杆高h,国旗上升的速度为v,根据国旗离旗杆顶端的距离S=旗杆的高度﹣国旗上升的距离,得出S=h﹣vt,再利用一次函数的性质即可求解.2·1·c·n·j·y
解:设旗杆高h,国旗上升的速度为v,国旗离旗杆顶端的距离为S,
根据题意,得S=h﹣vt,
∵h、v是常数,
∴S是t的一次函数,
∵S=﹣vt+h,﹣v<0,
∴S随v的增大而减小.
故选A.
4.【答案】:A
【解析】:考点 两条直线相交或平行问题.
分析 根据k的符号来求确定一次函数y=kx+b的图象所经过的象限,然后根据b的情况即可求得交点的位置.
解:∵一次函数y=kx+5中k>0,
∴一次函数y=kx+5的图象经过第一、二、三象限.
又∵一次函数y=k′x+7中k′<0,
∴一次函数y=k′x+7的图象经过第一、二、四象限.
∵5<7,
∴这两个一次函数的图象的交点在第一象限,
故选A.
5.【答案】:C
【解析】:考点 一次函数的增减性
解:∵直线的系数k =—4
∴y随着x的增大而减小
∴
故选C
6.【答案】:B
【解析】:考点 一次函数的应用.
分析 根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
解:如图,
设直线AB的解析式为y=kx+b,则
,
解得.
故直线AB的解析式为y=450x﹣600,
当x=2时,y=450×2﹣600=300,
300÷2=150(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m2.
故选B
7.【答案】:D
【解析】:考点 一次函数图像的平移
解:
8.【答案】:C
【解析】:考点 一次函数图象上点的坐标特征;轴对称-最短路线问题.
分析 根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
令y=x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=x+4中y=0,则x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣3,2),D′(0,﹣2),
∴有,解得:,
∴直线CD′的解析式为y=﹣x﹣2.
令y=﹣x﹣2中y=0,则0=﹣x﹣2,解得:x=﹣,
∴点P的坐标为(﹣,0).
故选C.
10.【答案】:B
【解析】:考点 动点问题的函数图象.
分析 根据点P在AD、DE、EF、FG、GB上时,△ABP的面积S与时间t的关系确定函数图象.
解: 解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
故选:B.
点评: 本题考查的是动点问题的函数图象,正确分析点P在不同的线段上△ABP的面积S与时间t的关系是解题的关键.
二、填空题
11.【答案】:二、四
【解析】:分析 根据正比例函数定义可得:|m|=1,且m﹣1≠0,计算出m的值,然后可得解析式,再根据正比例函数的性质可得答案.
解:由题意得:|m|=1,且m﹣1≠0,
解得:m=﹣1,
函数解析式为y=﹣2x,
∵k=﹣2<0,
∴该函数的图象经过第二、四象限.
故答案为:二、四.
点评:此题主要考查了正比例函数的定义和性质,关键是掌握形如y=kx(k是常数,k≠0)的函数叫做正比例函数;正比例函数y=kx(k是常数,k≠0),当k>0时,直线y=kx依次经过第三、一象限,从左向右上升,y随x的增大而增大;当k<0时,直线y=kx依次经过第二、四象限,从左向右下降,y随x的增大而减小.
12.【答案】:>3
【解析】:考点 一次函数与一元一次不等式
解:由图象得到直线y=x+b与直线y=kx+6的交点P(3,5),在点P(3,5)的右侧,直线y=x+b落在直线y=kx+6的上方,该部分对应的x的取值范围为x>3,即不等式x+b>kx+6的解集是x>3.
点拨:本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=x+b的值大于y=kx+6的自变量x的取值范围;从函数图象的角度看,就是确定直线y=x+b在直线y=kx+6的上方的部分所有的点的横坐标所构成的集合.
13.【答案】:一
【解析】:考点 一次函数图像确定方法
分析 首先确定点M所处的象限,然后确定k的符号,从而确定一次函数所经过的象限,得到答案.
解:∵点M(k﹣1,k+1)关于y轴的对称点在第四象限内,
∴点M(k﹣1,k+1)位于第三象限,
∴k﹣1<0且k+1<0,
解得:k<﹣1,
∴y=(k﹣1)x+k经过第二、三、四象限,不经过第一象限,
故答案为:一.
点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0,b<0时,函数图象经过二、三、四象限.
14.【答案】:(21008,21009).
【解析】:考点 一次函数图象上点的坐标特征;规律型;一次函数的应用.
试题分析 观察,发现规律:(1,2),(﹣2,2),(﹣2,﹣4),(4,﹣4),(4,8),…,∴(,)(n为自然数).
∵2017=1008×2+1,∴的坐标为((﹣2)1008,2(﹣2)1008)=(21008,21009).
故答案为:(21008,21009).
三、解答题
15.【答案】:(1)如下图;(2)①2;②该函数有最大值
【解析】:考点 函数图象,开放式数学问题。
解:
(1)如下图:
(2)①2(2.1到1.8之间都正确)
②该函数有最大值(其他正确性质都可以)。
16.【答案】:(1)y2=40(x﹣1)(1≤x≤2)(2)如图 (3)由图象得到达老家
【解析】:考点 一次函数的应用
解:(1)由题意,得y1=20x (0≤x≤2)
y2=40(x﹣1)(1≤x≤2);
(2)由题意得;
(3)由图象得到达老家.
17.【答案】:(1)() (2)150千克
【解析】: 考点 一次函数的应用
解:(1)设关于的函数解析式为(),
由线段过点和点,得,解得,
所以关于的函数解析式为();
(2)设关于的函数解析式为(),
由题意,得,即 ∴;
当时,(千克),
当时,(千克),
答:如果、两种机器人各连续搬运5小时,那么种机器人比种机器人多搬运了150千克
【答案】:(1)m =10,n =50 (2)yA=
(3)选择B方式上网学习合算
【解析】:
考点
一次函数的应用..
分析
(1)由图象知:m=10,n=50;
(2)根据已知条件即可求得yA与x之间的函数关系式为:当x≤25时,yA=25;当x>25时,yA=7+(x﹣25)×0.01,
(3)先求出yB与x之间函数关系为:当x≤50时,yB=10;当x>50时,yB=10+(x﹣50)×0.01=0.01x+9.5;然后分段求出哪种方式上网学习合算即可.
解:(1)由图象知:m=10,n=50;
(2)yA与x之间的函数关系式为:
当x≤25时,yA=25,
当x>25时,yA=7+(x﹣25)×0.01,
∴yA=0.01x+6.75,
∴yA=;
(3)∵yB与x之间函数关系为:当x≤50时,yB=10,
当x>50时,yB=10+(x﹣50)×0.01=0.01x+9.5
当0<x≤25时,yA=25,yB=50,
∴yA<yB,
∴选择A方式上网学习合算,
当25<x≤50时.yA=yB,即0.01x+6.75=10,解得;x=32.5,
∴当25<x<32.5时,yA<yB,选择A方式上网学习合算,
当x=32.5时,yA=yB,选择哪种方式上网学习都行,
当32.5<x≤50,yA>yB,选择B方式上网学习合算,
当x>50时,∵yA=0.01x+6.75,yB=0.01x+9.5,yA<yB,∴选择A方式上网学习合算,
综上所述:当0<x<32.5或x>50时,yA<yB,选择A方式上网学习合算,
当x=32.5时,yA=yB,选择哪种方式上网学习都行,
当32.5<x≤50时,yA>yB,选择B方式上网学习合算.
点评:
本题考查了一次函数的应用,得到两种收费方式的关系式是解决本题的关键.注意较合算的收费的方式应通过具体值的代入得到结果.
19.【答案】:(1)甲车从A地到达B地行驶了2.5小时(2)乙车到达时,甲车距离A地175千米.
【解析】:考点 一次函数的图象,二元一次方程组。
解 :(1)180÷1.5=120千米/时
300÷120=2.5时
甲车从A地到达B地行驶了2.5小时
(2)设所求函数关系式为y=kx+b(k≠0),将点(2.5,300),(5.5,0)代入,得
解得 ∴y=﹣100x+550(2.5≤x≤5.5)
(2)(300-180)÷1.5=80(千米/时)
300÷80=3.75(时)
当x=3.75时,y甲=175.
答:乙车到达时,甲车距离A地175千米.
第六章《一次函数》
班级: 姓名: 得分:
(时间90分钟 满分100分)
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.(2016广西南宁)下列各曲线中表示y是x的函数的是( )
A. B. C. D.
2. 下列函数表达式中是一次函数的是( )
A. B. C. D.
3.(2016?六盘水)为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列哪个函数图象能近似地刻画上升的国旗离旗杆顶端的距离与时间的关系( )
A. B.
C. D.
4. (2016·陕西)已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 直线上有两点,点A(—2,),点B(3,),则和的大小关系( )
A. B. C. D.无法判定
6. (2016?哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300m2B.150m2C.330m2D.450m2
7. 把函数的图像向右平移2个单位长度后的函数图像的解析式为( )
A. B. C. D.
8. (2016?包头)如图,直线y=x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0) B.(﹣6,0) C.(﹣,0) D.(﹣,0)
一次函数与的图像正确的是( )
10. (2015?江苏盐城)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分)
11. (2016·四川眉山)若函数是正比例函数,则该函数的图象经过第
象限.
12. (2016·山东省东营市)如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于的不等式的解集是_____________.
13. (2016·湖北荆州·)若点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数的图象不经过第 象限.
14. (2016?山东德州)如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线,,过点(1,0)作x轴的垂线交于点,过点作y轴的垂线交于点,过点作x轴的垂线交于点,过点作y轴的垂线交于点,…依次进行下去,则点的坐标为 .
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)
15. (本题满分6分)
(2016?北京)已知y是 的函数,自变量x的取值范围是> 0,下表是y与的几组对应值.
x
···
1
2
3
5
7
9
···
y
···
1.98
3.95
2.63
1.58
1.13
0.88
···
小腾根据学习函数的经验,利用上述表格所反映出的y与之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
根据画出的函数图象,写出:
x=4对应的函数值y约为____;
该函数的一条性质:_______________.
16. (本题满分6分)
(2016?山东滨州)星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
17. (本题满分9分)
(2016?上海)某物流公司引进、两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,种机器人于某日0时开始搬运,过了1小时,种机器人也开始搬运,如图,线段表示种机器人的搬运量(千克)与时间(时)的函数图像,线段表示种机器人的搬运量(千克)与(时)的函数图像,根据图像提供的信息,解答下列问题:
(1)求关于的函数解析式;
(2)如果、两种机器人各连续搬运5个小时,那么种机器人比种机器人多搬运了多少千克?
18. (本题满分9分)
(2015·湖北省潜江市、天门市、仙桃市、江汉油田)随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
7
25
0.01
B
m
n
0.01
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
19. (本题满分12分)
(2016?长春)甲、乙两车分别从A、B两地同时出发.甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
(1)求甲车从A地到达B地的行驶时间.
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求乙车到达A地时甲车距A地的路程.
20. (本题满分12分)
(2016?齐齐哈尔)有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.
〖鲁教版五四制七年级上数学单元测试卷〗
第六章《一次函数》答案与解析
3.【答案】:A
【解析】:考点 函数的图象.
分析 设旗杆高h,国旗上升的速度为v,根据国旗离旗杆顶端的距离S=旗杆的高度﹣国旗上升的距离,得出S=h﹣vt,再利用一次函数的性质即可求解.2·1·c·n·j·y
解:设旗杆高h,国旗上升的速度为v,国旗离旗杆顶端的距离为S,
根据题意,得S=h﹣vt,
∵h、v是常数,
∴S是t的一次函数,
∵S=﹣vt+h,﹣v<0,
∴S随v的增大而减小.
故选A.
4.【答案】:A
【解析】:考点 两条直线相交或平行问题.
分析 根据k的符号来求确定一次函数y=kx+b的图象所经过的象限,然后根据b的情况即可求得交点的位置.
解:∵一次函数y=kx+5中k>0,
∴一次函数y=kx+5的图象经过第一、二、三象限.
又∵一次函数y=k′x+7中k′<0,
∴一次函数y=k′x+7的图象经过第一、二、四象限.
∵5<7,
∴这两个一次函数的图象的交点在第一象限,
故选A.
5.【答案】:C
【解析】:考点 一次函数的增减性
解:∵直线的系数k =—4
∴y随着x的增大而减小
∴
故选C
6.【答案】:B
【解析】:考点 一次函数的应用.
分析 根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
解:如图,
设直线AB的解析式为y=kx+b,则
,
解得.
故直线AB的解析式为y=450x﹣600,
当x=2时,y=450×2﹣600=300,
300÷2=150(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是150m2.
故选B
7.【答案】:D
【解析】:考点 一次函数图像的平移
解:
8.【答案】:C
【解析】:考点 一次函数图象上点的坐标特征;轴对称-最短路线问题.
分析 根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
令y=x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=x+4中y=0,则x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣3,2),D′(0,﹣2),
∴有,解得:,
∴直线CD′的解析式为y=﹣x﹣2.
令y=﹣x﹣2中y=0,则0=﹣x﹣2,解得:x=﹣,
∴点P的坐标为(﹣,0).
故选C.
10.【答案】:B
【解析】:考点 动点问题的函数图象.
分析 根据点P在AD、DE、EF、FG、GB上时,△ABP的面积S与时间t的关系确定函数图象.
解: 解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小;
故选:B.
点评: 本题考查的是动点问题的函数图象,正确分析点P在不同的线段上△ABP的面积S与时间t的关系是解题的关键.
二、填空题
11.【答案】:二、四
【解析】:分析 根据正比例函数定义可得:|m|=1,且m﹣1≠0,计算出m的值,然后可得解析式,再根据正比例函数的性质可得答案.
解:由题意得:|m|=1,且m﹣1≠0,
解得:m=﹣1,
函数解析式为y=﹣2x,
∵k=﹣2<0,
∴该函数的图象经过第二、四象限.
故答案为:二、四.
点评:此题主要考查了正比例函数的定义和性质,关键是掌握形如y=kx(k是常数,k≠0)的函数叫做正比例函数;正比例函数y=kx(k是常数,k≠0),当k>0时,直线y=kx依次经过第三、一象限,从左向右上升,y随x的增大而增大;当k<0时,直线y=kx依次经过第二、四象限,从左向右下降,y随x的增大而减小.
12.【答案】:>3
【解析】:考点 一次函数与一元一次不等式
解:由图象得到直线y=x+b与直线y=kx+6的交点P(3,5),在点P(3,5)的右侧,直线y=x+b落在直线y=kx+6的上方,该部分对应的x的取值范围为x>3,即不等式x+b>kx+6的解集是x>3.
点拨:本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=x+b的值大于y=kx+6的自变量x的取值范围;从函数图象的角度看,就是确定直线y=x+b在直线y=kx+6的上方的部分所有的点的横坐标所构成的集合.
13.【答案】:一
【解析】:考点 一次函数图像确定方法
分析 首先确定点M所处的象限,然后确定k的符号,从而确定一次函数所经过的象限,得到答案.
解:∵点M(k﹣1,k+1)关于y轴的对称点在第四象限内,
∴点M(k﹣1,k+1)位于第三象限,
∴k﹣1<0且k+1<0,
解得:k<﹣1,
∴y=(k﹣1)x+k经过第二、三、四象限,不经过第一象限,
故答案为:一.
点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0,b<0时,函数图象经过二、三、四象限.
14.【答案】:(21008,21009).
【解析】:考点 一次函数图象上点的坐标特征;规律型;一次函数的应用.
试题分析 观察,发现规律:(1,2),(﹣2,2),(﹣2,﹣4),(4,﹣4),(4,8),…,∴(,)(n为自然数).
∵2017=1008×2+1,∴的坐标为((﹣2)1008,2(﹣2)1008)=(21008,21009).
故答案为:(21008,21009).
三、解答题
15.【答案】:(1)如下图;(2)①2;②该函数有最大值
【解析】:考点 函数图象,开放式数学问题。
解:
(1)如下图:
(2)①2(2.1到1.8之间都正确)
②该函数有最大值(其他正确性质都可以)。
16.【答案】:(1)y2=40(x﹣1)(1≤x≤2)(2)如图 (3)由图象得到达老家
【解析】:考点 一次函数的应用
解:(1)由题意,得y1=20x (0≤x≤2)
y2=40(x﹣1)(1≤x≤2);
(2)由题意得;
(3)由图象得到达老家.
17.【答案】:(1)() (2)150千克
【解析】: 考点 一次函数的应用
解:(1)设关于的函数解析式为(),
由线段过点和点,得,解得,
所以关于的函数解析式为();
(2)设关于的函数解析式为(),
由题意,得,即 ∴;
当时,(千克),
当时,(千克),
答:如果、两种机器人各连续搬运5小时,那么种机器人比种机器人多搬运了150千克
【答案】:(1)m =10,n =50 (2)yA=
(3)选择B方式上网学习合算
【解析】:
考点
一次函数的应用..
分析
(1)由图象知:m=10,n=50;
(2)根据已知条件即可求得yA与x之间的函数关系式为:当x≤25时,yA=25;当x>25时,yA=7+(x﹣25)×0.01,
(3)先求出yB与x之间函数关系为:当x≤50时,yB=10;当x>50时,yB=10+(x﹣50)×0.01=0.01x+9.5;然后分段求出哪种方式上网学习合算即可.
解:(1)由图象知:m=10,n=50;
(2)yA与x之间的函数关系式为:
当x≤25时,yA=25,
当x>25时,yA=7+(x﹣25)×0.01,
∴yA=0.01x+6.75,
∴yA=;
(3)∵yB与x之间函数关系为:当x≤50时,yB=10,
当x>50时,yB=10+(x﹣50)×0.01=0.01x+9.5
当0<x≤25时,yA=25,yB=50,
∴yA<yB,
∴选择A方式上网学习合算,
当25<x≤50时.yA=yB,即0.01x+6.75=10,解得;x=32.5,
∴当25<x<32.5时,yA<yB,选择A方式上网学习合算,
当x=32.5时,yA=yB,选择哪种方式上网学习都行,
当32.5<x≤50,yA>yB,选择B方式上网学习合算,
当x>50时,∵yA=0.01x+6.75,yB=0.01x+9.5,yA<yB,∴选择A方式上网学习合算,
综上所述:当0<x<32.5或x>50时,yA<yB,选择A方式上网学习合算,
当x=32.5时,yA=yB,选择哪种方式上网学习都行,
当32.5<x≤50时,yA>yB,选择B方式上网学习合算.
点评:
本题考查了一次函数的应用,得到两种收费方式的关系式是解决本题的关键.注意较合算的收费的方式应通过具体值的代入得到结果.
19.【答案】:(1)甲车从A地到达B地行驶了2.5小时(2)乙车到达时,甲车距离A地175千米.
【解析】:考点 一次函数的图象,二元一次方程组。
解 :(1)180÷1.5=120千米/时
300÷120=2.5时
甲车从A地到达B地行驶了2.5小时
(2)设所求函数关系式为y=kx+b(k≠0),将点(2.5,300),(5.5,0)代入,得
解得 ∴y=﹣100x+550(2.5≤x≤5.5)
(2)(300-180)÷1.5=80(千米/时)
300÷80=3.75(时)
当x=3.75时,y甲=175.
答:乙车到达时,甲车距离A地175千米.
