第一章《丰富的图形世界》单元检测题B
文档属性
| 名称 | 第一章《丰富的图形世界》单元检测题B |  | |
| 格式 | zip | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-18 16:08:29 | ||
图片预览

文档简介
2016--2017学年度北师版数学七年级第一学期单元检测题B
第一章《丰富的图形世界》
一.选择题(共12小题)
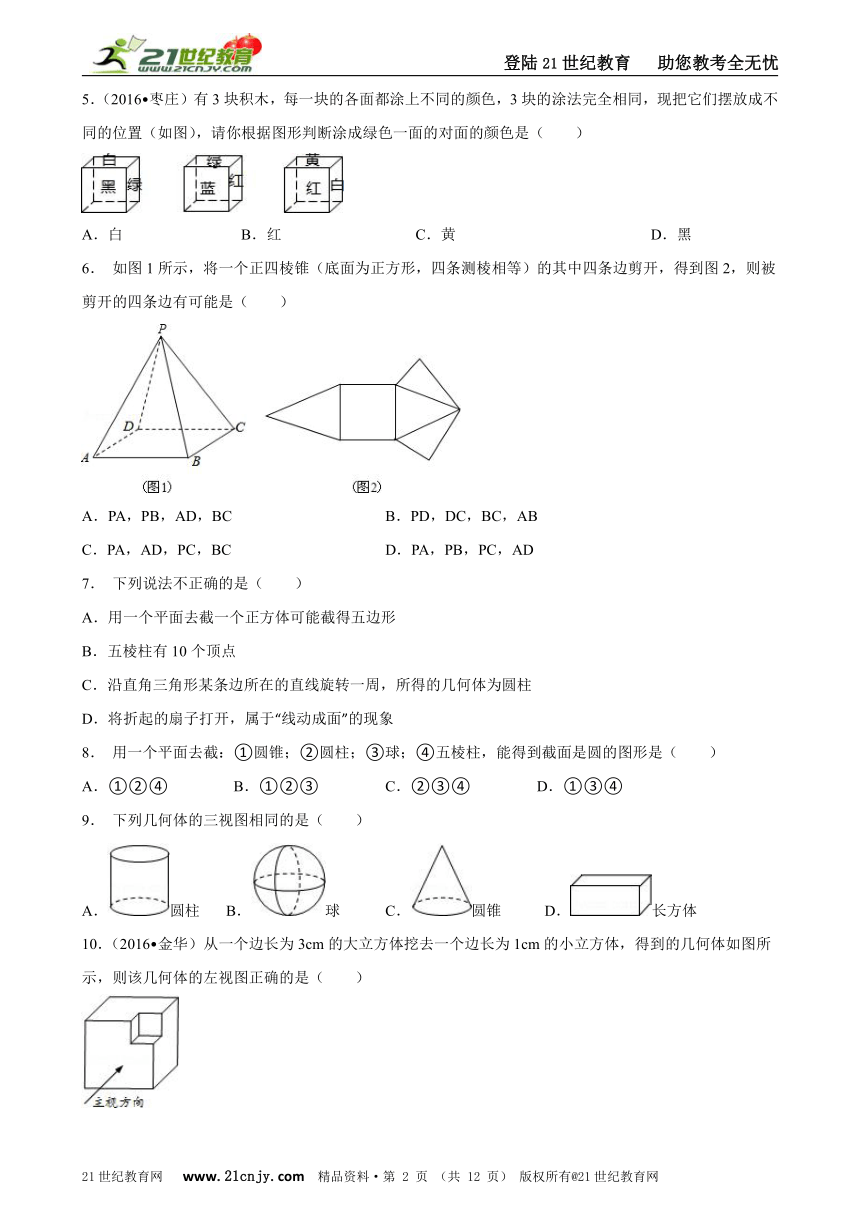
1. 将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
A. B. C. D.
2. 下列第一行所示的四个图形,每个图形均是由四种简单的图形a、b、c、d(圆、直线、三角形、长方形)中的两种组成.例如由a、b组成的图形记作a⊙b,那么由此可知,下列第二行的图中可以记作a⊙d的是( )www-2-1-cnjy-com
A. B. C. D.
3. 下面的几何体中,属于棱柱的有( )
A.1个 B.2个 C.3个 D.4个
4.(2016?安顺)如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
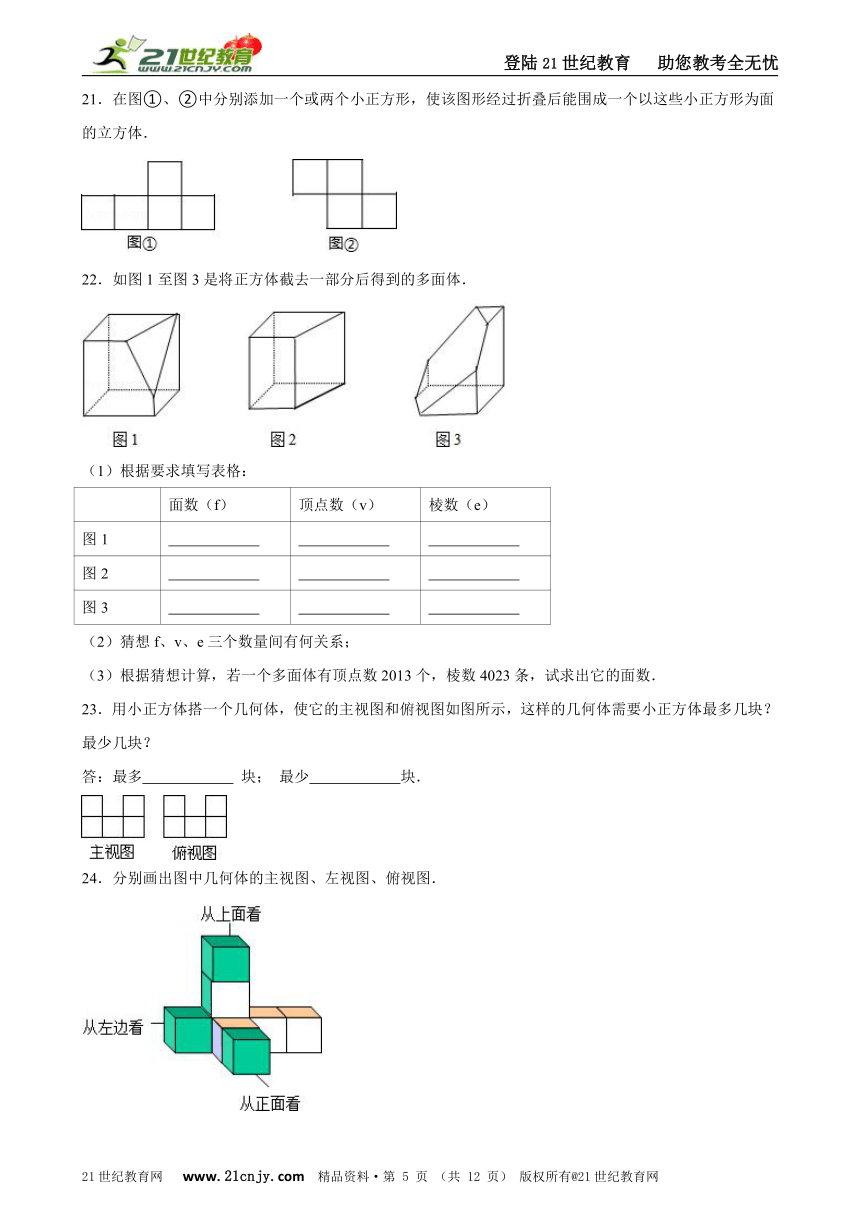
A.的 B.中 C.国 D.梦
5.(2016?枣庄)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
A.白 B.红 C.黄 D.黑
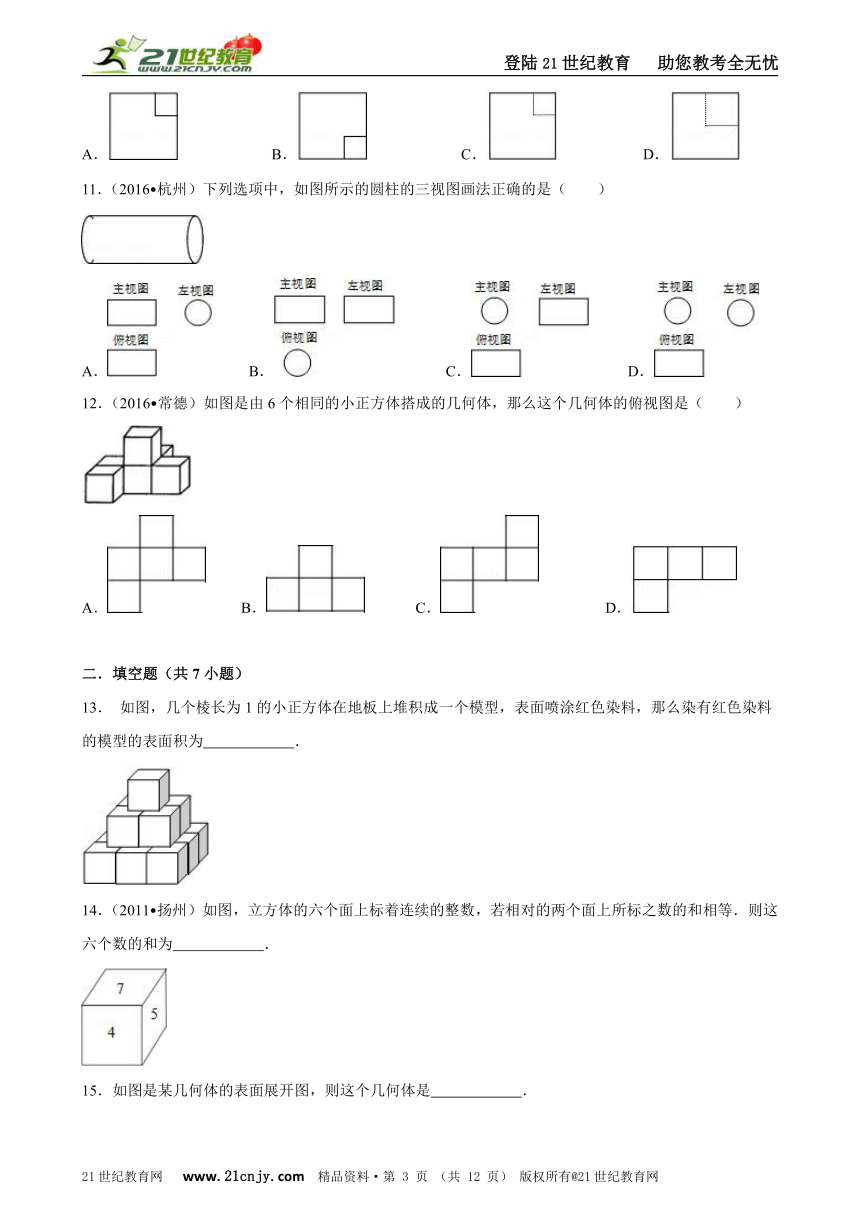
6. 如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
A.PA,PB,AD,BC B.PD,DC,BC,AB
C.PA,AD,PC,BC D.PA,PB,PC,AD
7. 下列说法不正确的是( )
A.用一个平面去截一个正方体可能截得五边形
B.五棱柱有10个顶点
C.沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆柱
D.将折起的扇子打开,属于“线动成面”的现象
8. 用一个平面去截:①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是( )
A.①②④ B.①②③ C.②③④ D.①③④
9. 下列几何体的三视图相同的是( )
A.圆柱 B.球 C.圆锥 D.长方体
10.(2016?金华)从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )【出处:21教育名师】
A. B. C. D.
11.(2016?杭州)下列选项中,如图所示的圆柱的三视图画法正确的是( )
A. B. C. D.
12.(2016?常德)如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
A. B. C. D.
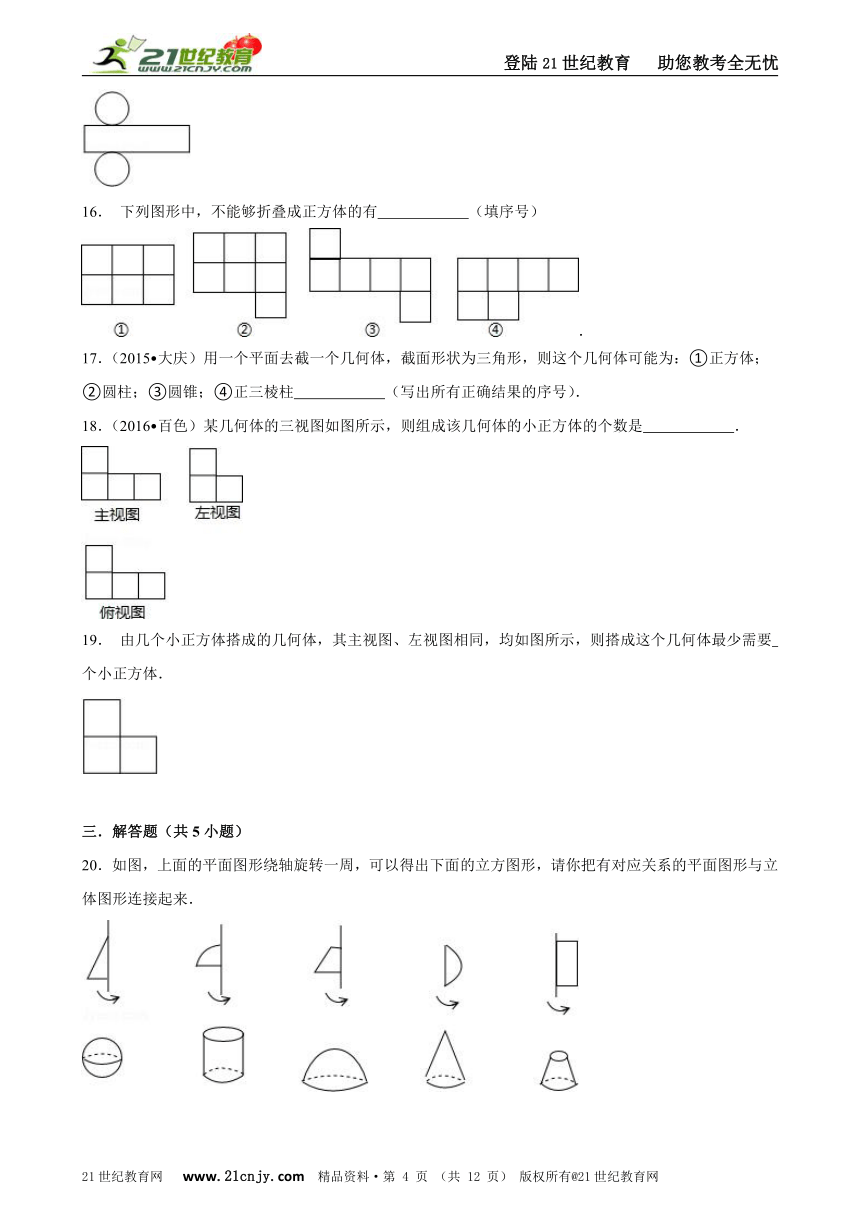
二.填空题(共7小题)
13. 如图,几个棱长为1的小正方体在地板上堆积成一个模型,表面喷涂红色染料,那么染有红色染料的模型的表面积为 .2-1-c-n-j-y
14.(2011?扬州)如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等.则这六个数的和为 .
15.如图是某几何体的表面展开图,则这个几何体是 .
16. 下列图形中,不能够折叠成正方体的有 (填序号).
17.(2015?大庆)用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱 (写出所有正确结果的序号).21·cn·jy·com
18.(2016?百色)某几何体的三视图如图所示,则组成该几何体的小正方体的个数是 .
19. 由几个小正方体搭成的几何体,其主视图、左视图相同,均如图所示,则搭成这个几何体最少需要 个小正方体.
三.解答题(共5小题)
20.如图,上面的平面图形绕轴旋转一周,可以得出下面的立方图形,请你把有对应关系的平面图形与立体图形连接起来.
21.在图①、②中分别添加一个或两个小正方形,使该图形经过折叠后能围成一个以这些小正方形为面的立方体.
22.如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
面数(f)
顶点数(v)
棱数(e)
图1
图2
图3
(2)猜想f、v、e三个数量间有何关系;
(3)根据猜想计算,若一个多面体有顶点数2013个,棱数4023条,试求出它的面数.
23.用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体需要小正方体最多几块?最少几块?21世纪教育网版权所有
答:最多 块; 最少 块.
24.分别画出图中几何体的主视图、左视图、俯视图.
答案与解析
一.选择题(共12小题)
1.【分析】根据面动成体以及圆台的特点,即可解答.
【解答】解:绕直线l旋转一周,可以得到的圆台,
故选:C.
2【分析】结合已知图形,先判断a,b,c,d所代表的图形,再判断记作a⊙d的图形即可.
【解答】解:根据题意,知a代表长方形,d代表直线,所以记作a⊙d的图形是长方形和直线的组合,故选A.【来源:21·世纪·教育·网】
3.【分析】根据有两个面平行,其余各面都是平行四边形,并且每相邻两个平行四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱,可得答案.www.21-cn-jy.com
【解答】解:从左到右依次是长方体,圆柱,棱柱,棱锥,圆锥,棱柱.
故选:C.
4.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“们”与“中”是相对面,
“我”与“梦”是相对面,
“的”与“国”是相对面.
故选:D.
5.【分析】根据图形可得涂有绿色一面的邻边是白,黑,红,蓝,即可得到结论.
【解答】解:∵涂有绿色一面的邻边是白,黑,红,蓝,
∴涂成绿色一面的对面的颜色是黄色,
故选C.
6.【分析】根据图2中正方形左边的三角形可知需剪开PA、PB,根据正方形右边三个三角形脱离正方形的上下两边可知需剪开AD、BC,可得答案.21cnjy.com
【解答】解:根据图2中的展开图可知,底面正方形ABCD的左边一个三角形是独立的,
据此可知,需剪开图1中的PA、PB,
根据正方形右边三个三角形脱离正方形的上下两边可知,
需剪开AD、BC,
综上,被剪开的四条边可能是:PA、PB、AD、BC,
故选:A.
7.【分析】根据几何体的特征以及面动成体、线动成面的概念进行判断即可.
【解答】解:(A)用一个平面去截一个正方体,截面可能为三角形、四边形、五边形或六边形,故(A)正确;21·世纪*教育网
(B)五棱柱的上下底面上各有5个顶点,所以共有10个顶点,故(B)正确;
(C)沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆锥或底面重合的两个圆锥,故(C)错误;
(D)将折起的扇子打开,属于“线动成面”的现象,故(D)正确.
故选(C)
8.【分析】根据圆锥、圆柱、球、五棱柱的形状特点判断即可.
【解答】解:圆锥,如果截面与底面平行,那么截面就是圆;
圆柱,如果截面与上下面平行,那么截面是圆;
球,截面一定是圆;
五棱柱,无论怎么去截,截面都不可能有弧度.
故选B.
9.【分析】找出圆柱,球,圆锥,以及长方体的三视图,即可做出判断.
【解答】解:A、圆柱的三视图,如图所示,不合题意;
B、球的三视图,如图所示,符合题意;
C、圆锥的三视图,如图所示,不合题意;
D、长方体的三视图,如图所示,不合题意;
.
故选B
10.【分析】直接利用左视图的观察角度,进而得出视图.
【解答】解:如图所示:∵从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,
∴该几何体的左视图为:.
故选:C.
11.【分析】根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,可得答案.21教育网
【解答】解:该圆柱体的主视图、俯视图均为矩形,左视图为圆,
故选:A.
12.【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得上面第一层中间有1个正方形,第二层有3个正方形.下面一层左边有1个正方形,
故选A.
二.填空题(共7小题)
13.【分析】分别从上、下、左、右、前、后6个方向观察可以求出表面积.
【解答】解:∵从上下观察共有18个面,左右观察共有12个面,前后观察共有12个面,
∴一共有42个面,每个面的面积=1×1=1,
∴染有红色染料的模型的表面积为42.
故答案为42.
14.【分析】由题意“六个连续的整数”“两个相对面上的数字和相等”,则由4,5,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8或4,5,6,7,8,9,因为相对面上的数字和相等,所以第一种情况必须是4,5相对,第二种情况必须是4,7相对,故这六个数字只能是4,5,6,7,8,9,再求出这六个数的和即可.2·1·c·n·j·y
【解答】解:从4,5,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8或4,5,6,7,8,9, 21*cnjy*com
因为相对面上的数字和相等,所以第一种情况必须是4,5处于对面,
第二种情况必须是4,7处于对面,
故这六个数字只能是4,5,6,7,8,9,
所以这六个数的和为4+5+6+7+8+9=39.
故答案为:39.
15.【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:一个长方形和两个圆折叠后,能围成的几何体是圆柱.
故答案为:圆柱体.
16.【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:只有③经过折叠能围成正方体,
所以不能够折叠成正方体的有①②④,
故答案为:①②④.
17.【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.
【解答】解:①正方体能截出三角形;
②圆柱不能截出三角形;
③圆锥沿着母线截几何体可以截出三角形;
④正三棱柱能截出三角形.
故截面可能是三角形的有3个.
故答案为:①③④.
18.【分析】根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两行3列,故可得出该几何体的小正方体的个数.【来源:21cnj*y.co*m】
【解答】解:综合三视图,我们可得出,这个几何体的底层应该有4个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为4+1=5个;
故答案为:5.
19.【分析】根据所给出的图形可知这个几何体共有2层,2列,先看第一层正方体可能的最少个数,再看第二层正方体的可能的最少个数,相加即可.【版权所有:21教育】
【解答】解:仔细观察物体的主视图和左视图可知:该几何体的下面最少要有2个小正方体,上面最少要有1个小正方体,21教育名师原创作品
故该几何体最少有3个小正方体组成.
故答案为:3.
三.解答题(共5小题)
20.【分析】根据“面动成体”的原理,结合图形特征进行旋转,判断出旋转后的立体图形即可.
【解答】解:连线如下:
21.【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【解答】解:(1)图①,添加后如图所示
(2)图②,添加后如图所示
22.【分析】(1)根据图形数出即可.
(2)根据(1)中结果得出f+v﹣e=2.
(3)代入f+v﹣e=2求出即可.
【解答】解:(1)题1,面数f=7,顶点数v=9,棱数e=14,
题2,面数f=6,顶点数v=8,棱数e=12,
题3,面数f=7,顶点数v=10,棱数e=15,
故答案为:7,9,14.6,8,12,7,10,15.
(2)f+v﹣e=2.
(3)∵v=2013,e=4023,f+v﹣e=2
∴f+2013﹣4023=2,
f=2012,
即它的面数是2012.
23.【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从而算出总的个数.21*cnjy*com
【解答】解:由俯视图可得最底层有5个小正方体,
由主视图可得第一列和第三列最多有4个正方体,
那么最少需要5+4=9个正方体.
由俯视图可得最底层有5个小正方体,
由主视图可得第一列和第三列最少有2个正方体,
那么最少需要5+2=7个正方体.
故答案为:9,7
24.【分析】从正面看从左往右4列正方形的个数依次为1,3,1,1;
从左面看从左往右3列正方形的个数依次为3,1,1;
从上面看从左往右4列正方形的个数依次为1,3,1,1.
【解答】解:
第一章《丰富的图形世界》
一.选择题(共12小题)
1. 将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
A. B. C. D.
2. 下列第一行所示的四个图形,每个图形均是由四种简单的图形a、b、c、d(圆、直线、三角形、长方形)中的两种组成.例如由a、b组成的图形记作a⊙b,那么由此可知,下列第二行的图中可以记作a⊙d的是( )www-2-1-cnjy-com
A. B. C. D.
3. 下面的几何体中,属于棱柱的有( )
A.1个 B.2个 C.3个 D.4个
4.(2016?安顺)如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
A.的 B.中 C.国 D.梦
5.(2016?枣庄)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
A.白 B.红 C.黄 D.黑
6. 如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
A.PA,PB,AD,BC B.PD,DC,BC,AB
C.PA,AD,PC,BC D.PA,PB,PC,AD
7. 下列说法不正确的是( )
A.用一个平面去截一个正方体可能截得五边形
B.五棱柱有10个顶点
C.沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆柱
D.将折起的扇子打开,属于“线动成面”的现象
8. 用一个平面去截:①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是( )
A.①②④ B.①②③ C.②③④ D.①③④
9. 下列几何体的三视图相同的是( )
A.圆柱 B.球 C.圆锥 D.长方体
10.(2016?金华)从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )【出处:21教育名师】
A. B. C. D.
11.(2016?杭州)下列选项中,如图所示的圆柱的三视图画法正确的是( )
A. B. C. D.
12.(2016?常德)如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
A. B. C. D.
二.填空题(共7小题)
13. 如图,几个棱长为1的小正方体在地板上堆积成一个模型,表面喷涂红色染料,那么染有红色染料的模型的表面积为 .2-1-c-n-j-y
14.(2011?扬州)如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等.则这六个数的和为 .
15.如图是某几何体的表面展开图,则这个几何体是 .
16. 下列图形中,不能够折叠成正方体的有 (填序号).
17.(2015?大庆)用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱 (写出所有正确结果的序号).21·cn·jy·com
18.(2016?百色)某几何体的三视图如图所示,则组成该几何体的小正方体的个数是 .
19. 由几个小正方体搭成的几何体,其主视图、左视图相同,均如图所示,则搭成这个几何体最少需要 个小正方体.
三.解答题(共5小题)
20.如图,上面的平面图形绕轴旋转一周,可以得出下面的立方图形,请你把有对应关系的平面图形与立体图形连接起来.
21.在图①、②中分别添加一个或两个小正方形,使该图形经过折叠后能围成一个以这些小正方形为面的立方体.
22.如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
面数(f)
顶点数(v)
棱数(e)
图1
图2
图3
(2)猜想f、v、e三个数量间有何关系;
(3)根据猜想计算,若一个多面体有顶点数2013个,棱数4023条,试求出它的面数.
23.用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体需要小正方体最多几块?最少几块?21世纪教育网版权所有
答:最多 块; 最少 块.
24.分别画出图中几何体的主视图、左视图、俯视图.
答案与解析
一.选择题(共12小题)
1.【分析】根据面动成体以及圆台的特点,即可解答.
【解答】解:绕直线l旋转一周,可以得到的圆台,
故选:C.
2【分析】结合已知图形,先判断a,b,c,d所代表的图形,再判断记作a⊙d的图形即可.
【解答】解:根据题意,知a代表长方形,d代表直线,所以记作a⊙d的图形是长方形和直线的组合,故选A.【来源:21·世纪·教育·网】
3.【分析】根据有两个面平行,其余各面都是平行四边形,并且每相邻两个平行四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱,可得答案.www.21-cn-jy.com
【解答】解:从左到右依次是长方体,圆柱,棱柱,棱锥,圆锥,棱柱.
故选:C.
4.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“们”与“中”是相对面,
“我”与“梦”是相对面,
“的”与“国”是相对面.
故选:D.
5.【分析】根据图形可得涂有绿色一面的邻边是白,黑,红,蓝,即可得到结论.
【解答】解:∵涂有绿色一面的邻边是白,黑,红,蓝,
∴涂成绿色一面的对面的颜色是黄色,
故选C.
6.【分析】根据图2中正方形左边的三角形可知需剪开PA、PB,根据正方形右边三个三角形脱离正方形的上下两边可知需剪开AD、BC,可得答案.21cnjy.com
【解答】解:根据图2中的展开图可知,底面正方形ABCD的左边一个三角形是独立的,
据此可知,需剪开图1中的PA、PB,
根据正方形右边三个三角形脱离正方形的上下两边可知,
需剪开AD、BC,
综上,被剪开的四条边可能是:PA、PB、AD、BC,
故选:A.
7.【分析】根据几何体的特征以及面动成体、线动成面的概念进行判断即可.
【解答】解:(A)用一个平面去截一个正方体,截面可能为三角形、四边形、五边形或六边形,故(A)正确;21·世纪*教育网
(B)五棱柱的上下底面上各有5个顶点,所以共有10个顶点,故(B)正确;
(C)沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆锥或底面重合的两个圆锥,故(C)错误;
(D)将折起的扇子打开,属于“线动成面”的现象,故(D)正确.
故选(C)
8.【分析】根据圆锥、圆柱、球、五棱柱的形状特点判断即可.
【解答】解:圆锥,如果截面与底面平行,那么截面就是圆;
圆柱,如果截面与上下面平行,那么截面是圆;
球,截面一定是圆;
五棱柱,无论怎么去截,截面都不可能有弧度.
故选B.
9.【分析】找出圆柱,球,圆锥,以及长方体的三视图,即可做出判断.
【解答】解:A、圆柱的三视图,如图所示,不合题意;
B、球的三视图,如图所示,符合题意;
C、圆锥的三视图,如图所示,不合题意;
D、长方体的三视图,如图所示,不合题意;
.
故选B
10.【分析】直接利用左视图的观察角度,进而得出视图.
【解答】解:如图所示:∵从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,
∴该几何体的左视图为:.
故选:C.
11.【分析】根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,可得答案.21教育网
【解答】解:该圆柱体的主视图、俯视图均为矩形,左视图为圆,
故选:A.
12.【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得上面第一层中间有1个正方形,第二层有3个正方形.下面一层左边有1个正方形,
故选A.
二.填空题(共7小题)
13.【分析】分别从上、下、左、右、前、后6个方向观察可以求出表面积.
【解答】解:∵从上下观察共有18个面,左右观察共有12个面,前后观察共有12个面,
∴一共有42个面,每个面的面积=1×1=1,
∴染有红色染料的模型的表面积为42.
故答案为42.
14.【分析】由题意“六个连续的整数”“两个相对面上的数字和相等”,则由4,5,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8或4,5,6,7,8,9,因为相对面上的数字和相等,所以第一种情况必须是4,5相对,第二种情况必须是4,7相对,故这六个数字只能是4,5,6,7,8,9,再求出这六个数的和即可.2·1·c·n·j·y
【解答】解:从4,5,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8或4,5,6,7,8,9, 21*cnjy*com
因为相对面上的数字和相等,所以第一种情况必须是4,5处于对面,
第二种情况必须是4,7处于对面,
故这六个数字只能是4,5,6,7,8,9,
所以这六个数的和为4+5+6+7+8+9=39.
故答案为:39.
15.【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:一个长方形和两个圆折叠后,能围成的几何体是圆柱.
故答案为:圆柱体.
16.【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:只有③经过折叠能围成正方体,
所以不能够折叠成正方体的有①②④,
故答案为:①②④.
17.【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.
【解答】解:①正方体能截出三角形;
②圆柱不能截出三角形;
③圆锥沿着母线截几何体可以截出三角形;
④正三棱柱能截出三角形.
故截面可能是三角形的有3个.
故答案为:①③④.
18.【分析】根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两行3列,故可得出该几何体的小正方体的个数.【来源:21cnj*y.co*m】
【解答】解:综合三视图,我们可得出,这个几何体的底层应该有4个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为4+1=5个;
故答案为:5.
19.【分析】根据所给出的图形可知这个几何体共有2层,2列,先看第一层正方体可能的最少个数,再看第二层正方体的可能的最少个数,相加即可.【版权所有:21教育】
【解答】解:仔细观察物体的主视图和左视图可知:该几何体的下面最少要有2个小正方体,上面最少要有1个小正方体,21教育名师原创作品
故该几何体最少有3个小正方体组成.
故答案为:3.
三.解答题(共5小题)
20.【分析】根据“面动成体”的原理,结合图形特征进行旋转,判断出旋转后的立体图形即可.
【解答】解:连线如下:
21.【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【解答】解:(1)图①,添加后如图所示
(2)图②,添加后如图所示
22.【分析】(1)根据图形数出即可.
(2)根据(1)中结果得出f+v﹣e=2.
(3)代入f+v﹣e=2求出即可.
【解答】解:(1)题1,面数f=7,顶点数v=9,棱数e=14,
题2,面数f=6,顶点数v=8,棱数e=12,
题3,面数f=7,顶点数v=10,棱数e=15,
故答案为:7,9,14.6,8,12,7,10,15.
(2)f+v﹣e=2.
(3)∵v=2013,e=4023,f+v﹣e=2
∴f+2013﹣4023=2,
f=2012,
即它的面数是2012.
23.【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数,从而算出总的个数.21*cnjy*com
【解答】解:由俯视图可得最底层有5个小正方体,
由主视图可得第一列和第三列最多有4个正方体,
那么最少需要5+4=9个正方体.
由俯视图可得最底层有5个小正方体,
由主视图可得第一列和第三列最少有2个正方体,
那么最少需要5+2=7个正方体.
故答案为:9,7
24.【分析】从正面看从左往右4列正方形的个数依次为1,3,1,1;
从左面看从左往右3列正方形的个数依次为3,1,1;
从上面看从左往右4列正方形的个数依次为1,3,1,1.
【解答】解:
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
