椭圆的标准方程课件
图片预览


文档简介
(共24张PPT)
椭圆及其标准方程
大庆第十三中学 王娜
2008年9月25日是什么日子?
设置情境 问题诱导
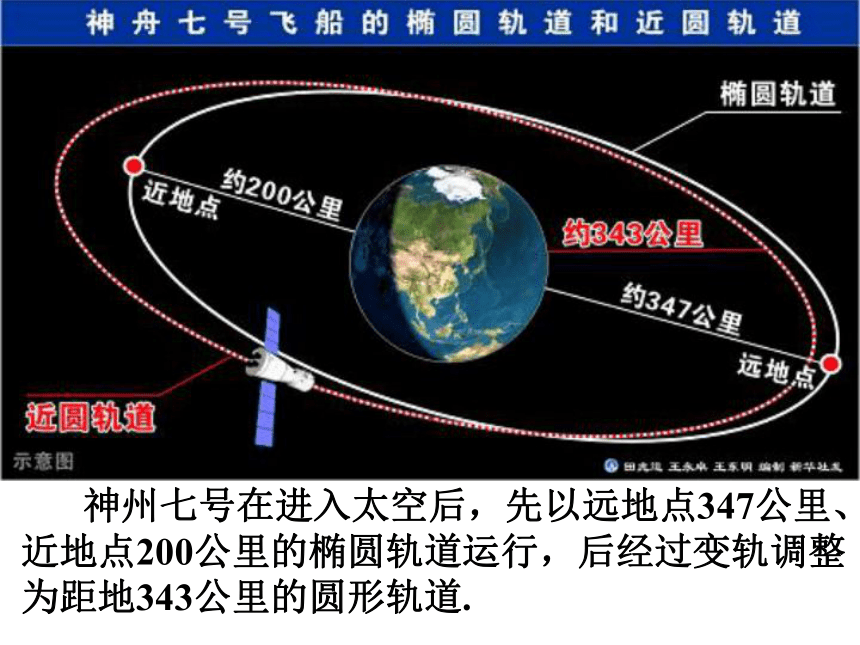
请问: “神舟七号”载人飞船的运行轨道是什么?
神州七号在进入太空后,先以远地点347公里、近地点200公里的椭圆轨道运行,后经过变轨调整为距地343公里的圆形轨道.
生活中的椭圆
认识椭圆
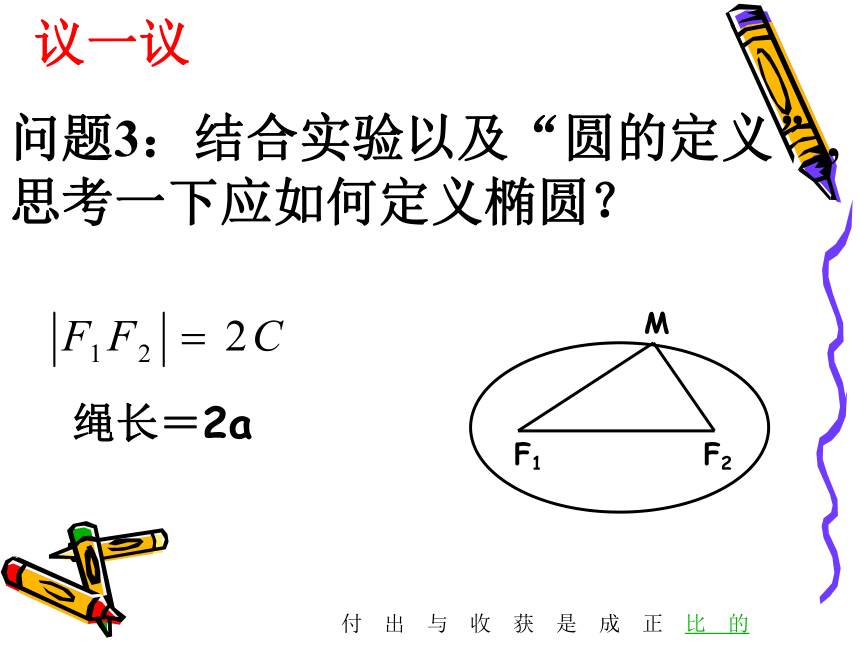
问题3:结合实验以及“圆的定义”,
思考一下应如何定义椭圆?
议一议
M
F1
F2
绳长=2a
付 出 与 收 获 是 成 正 比 的
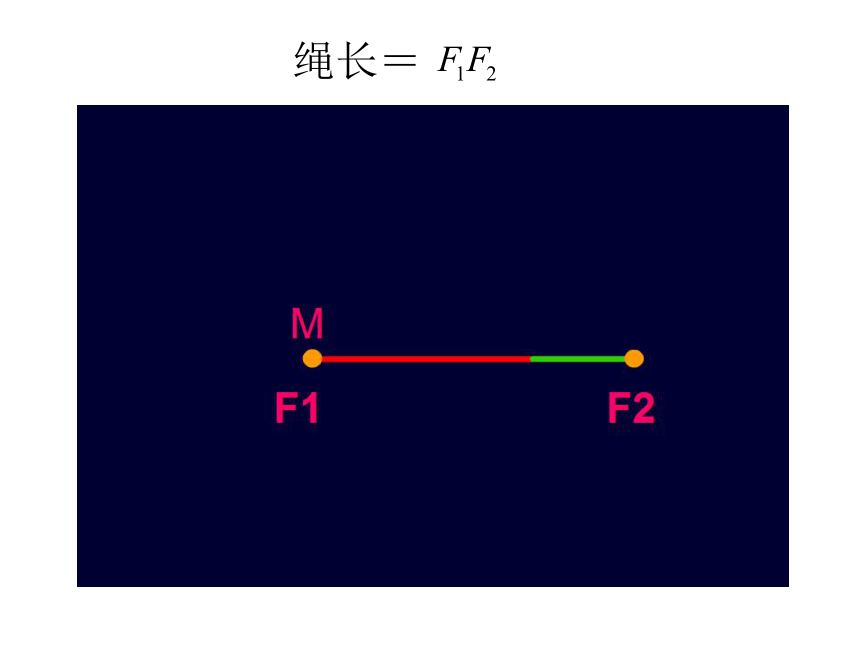
绳长=
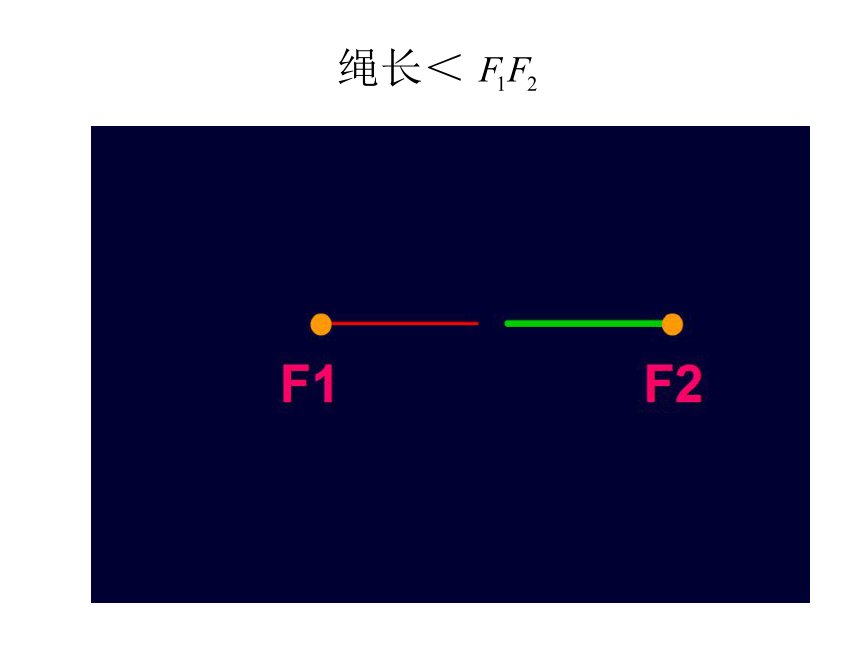
绳长<
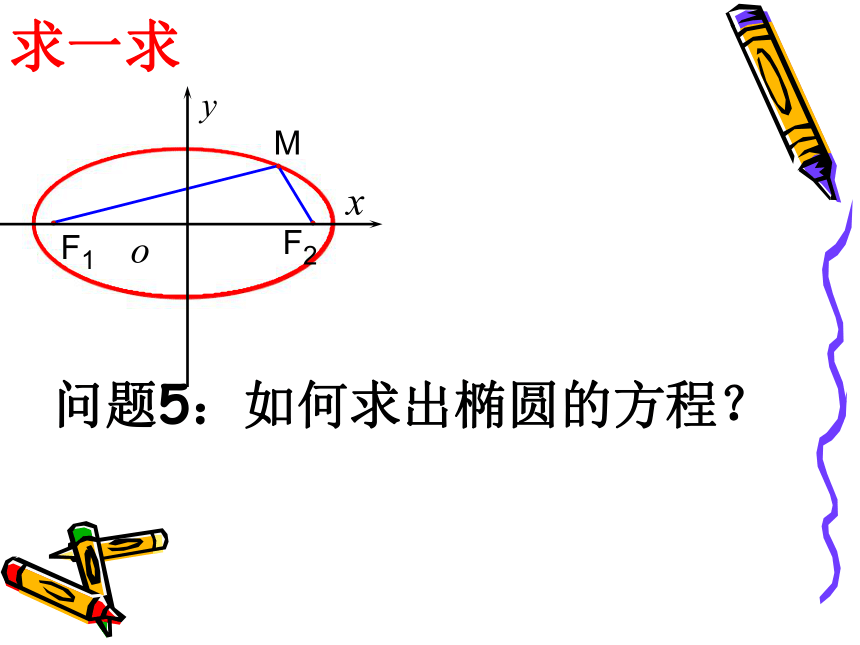
求一求
问题5:如何求出椭圆的方程?
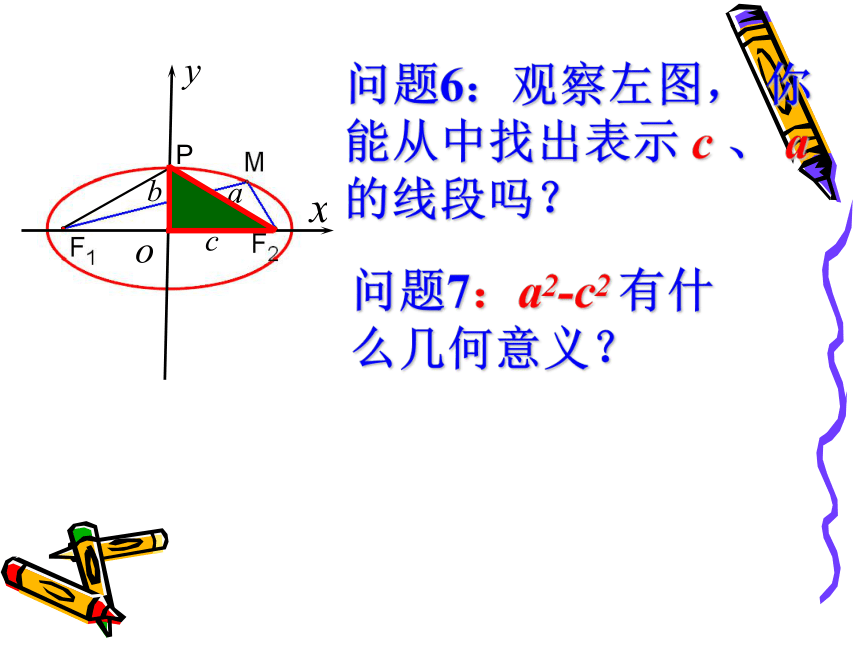
问题6:观察左图, 你能从中找出表示 c 、 a 的线段吗?
问题7:a2-c2 有什么几何意义?
问题8:如果所给椭圆如图所示,应如何建系?试猜想椭圆的标准方程呢?
F1
F2
M
用一用
1.试求出下列各椭圆中a,b,c的值,判断焦点位置并说出焦点坐标.
总结:在例1中你学到了哪些知识?
付 出 与 收 获 是 成 正 比 的
变式:下列方程哪些表示的是椭圆,如果是,判断它的焦点在哪个坐标轴上?
用一用
变式一:将上题焦点改为(0,-4)、(0,4), 结果如何?
(1)已知两个焦点的坐标分别是(-4,0)、(4,0), 椭圆上一点P到两焦点距离的和等于10;
用一用
2、写出适合下列条件的椭圆的标准方程
变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的距离和等于10,结果如何?
当焦点在X轴时,方程为:
当焦点在Y轴时,方程为:
试总结求椭圆标准方程的步骤?
变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的距离和等于10,结果如何?
当焦点在X轴时,方程为:
当焦点在Y轴时,方程为:
试总结求椭圆标准方程的步骤?
3、 两个焦点的坐标是( 0 ,-2)和 (0 ,2),并且经过点 P
试写出椭圆的标准方程。
典例分析
分母哪个大,焦点就在哪个轴上
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
探究定义
a、b、c 的关系
x
y
F1
F2
M
O
x
y
F1
F2
M
O
a2-c2=b2
(a>b>0)
谈谈收获
|MF1 |+|MF2|=2a(2a>2c).
练一练
1、用定义判断下列动点的M的轨迹是否为椭圆?
(1)到F1(-2,0),F2(2,0)的距离之
和为6的点的轨迹。
(2)到F1(0,-2),F2(0,2)的距离之
和为4的点的轨迹。
(3)到F1(-2,0),F2(2,0)的距离之
和为3 的点的轨迹。
3.写出适合下列条件的椭圆的标准方程:(1)a=4,b=3,焦点在x轴;
(2)a=5,c=2,焦点在y轴上.
2.椭圆
的焦距是 ,焦点坐
若CD为过F1的弦,则
的周长为 .
,a= b=
练一练
标为
1、课后反思与体验
课后作业
2、基础题:书上36页1,2,3,4题
1、本节课我学到了哪些知识,是用什么方法学会的?
2、我还有什么知识没有掌握,是什么原因导致的?
3、我从老师和同学那儿学到了哪些好的学习方法?
4、通过上述的回顾评价一下自己本节课的表现。
2009年3月21日,嫦娥一号撞月成功,这标志着什么?给了你什么启示?我们期待“嫦娥N号”中有你的成果。
欢迎大家提出宝贵意见!
谢
谢
结束
椭圆及其标准方程
大庆第十三中学 王娜
2008年9月25日是什么日子?
设置情境 问题诱导
请问: “神舟七号”载人飞船的运行轨道是什么?
神州七号在进入太空后,先以远地点347公里、近地点200公里的椭圆轨道运行,后经过变轨调整为距地343公里的圆形轨道.
生活中的椭圆
认识椭圆
问题3:结合实验以及“圆的定义”,
思考一下应如何定义椭圆?
议一议
M
F1
F2
绳长=2a
付 出 与 收 获 是 成 正 比 的
绳长=
绳长<
求一求
问题5:如何求出椭圆的方程?
问题6:观察左图, 你能从中找出表示 c 、 a 的线段吗?
问题7:a2-c2 有什么几何意义?
问题8:如果所给椭圆如图所示,应如何建系?试猜想椭圆的标准方程呢?
F1
F2
M
用一用
1.试求出下列各椭圆中a,b,c的值,判断焦点位置并说出焦点坐标.
总结:在例1中你学到了哪些知识?
付 出 与 收 获 是 成 正 比 的
变式:下列方程哪些表示的是椭圆,如果是,判断它的焦点在哪个坐标轴上?
用一用
变式一:将上题焦点改为(0,-4)、(0,4), 结果如何?
(1)已知两个焦点的坐标分别是(-4,0)、(4,0), 椭圆上一点P到两焦点距离的和等于10;
用一用
2、写出适合下列条件的椭圆的标准方程
变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的距离和等于10,结果如何?
当焦点在X轴时,方程为:
当焦点在Y轴时,方程为:
试总结求椭圆标准方程的步骤?
变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的距离和等于10,结果如何?
当焦点在X轴时,方程为:
当焦点在Y轴时,方程为:
试总结求椭圆标准方程的步骤?
3、 两个焦点的坐标是( 0 ,-2)和 (0 ,2),并且经过点 P
试写出椭圆的标准方程。
典例分析
分母哪个大,焦点就在哪个轴上
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
探究定义
a、b、c 的关系
x
y
F1
F2
M
O
x
y
F1
F2
M
O
a2-c2=b2
(a>b>0)
谈谈收获
|MF1 |+|MF2|=2a(2a>2c).
练一练
1、用定义判断下列动点的M的轨迹是否为椭圆?
(1)到F1(-2,0),F2(2,0)的距离之
和为6的点的轨迹。
(2)到F1(0,-2),F2(0,2)的距离之
和为4的点的轨迹。
(3)到F1(-2,0),F2(2,0)的距离之
和为3 的点的轨迹。
3.写出适合下列条件的椭圆的标准方程:(1)a=4,b=3,焦点在x轴;
(2)a=5,c=2,焦点在y轴上.
2.椭圆
的焦距是 ,焦点坐
若CD为过F1的弦,则
的周长为 .
,a= b=
练一练
标为
1、课后反思与体验
课后作业
2、基础题:书上36页1,2,3,4题
1、本节课我学到了哪些知识,是用什么方法学会的?
2、我还有什么知识没有掌握,是什么原因导致的?
3、我从老师和同学那儿学到了哪些好的学习方法?
4、通过上述的回顾评价一下自己本节课的表现。
2009年3月21日,嫦娥一号撞月成功,这标志着什么?给了你什么启示?我们期待“嫦娥N号”中有你的成果。
欢迎大家提出宝贵意见!
谢
谢
结束
