2.1.3分层抽样
图片预览








文档简介
课件29张PPT。分层抽样问题提出问题1:请选择最适合的抽样方法
(1)从10台冰箱中抽出3台进行质量检查.
(2)从学校的10000名学生中抽取100名进行健康体检.
(3)某地区有高中生2400人,初中生10800人,小学生11100人.当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查.
问题2:总体有什么特点?
问题3:样本中高中生,初中生,小学生都必须有吗?
问题4:样本中高中生,初中生,小学生哪个人数多?分别是多少?高中生: 2400*1%=24,
初中生: 10900*1%=109,
小学生: 11000*1%=110,知识探究:分层抽样的定义分层抽样:若总体由差异明显的几部分组成,抽样时,先将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,再将各层取出的个体合在一起作为样本.
问题3:试总结分层抽样有哪些注意事项?基础探索(1)有40件产品,其中一等品有10件,二等品有25件,次品有5件,现从中抽出8件进行质量分析。
问题4:要采取何种抽样方法?
问题5:抽样比是多少?
问题6: 样品中一等品,二等品,次品分别有多少?(2)某单位有职工500人,其中35岁以下的有125人,35岁~49岁的有280人,50岁以上的有95人.为了调查职工的身体状况,要从中抽取一个容量为100的样本.试确定用何种抽样方法并写出抽样过程。问题6:试总结分层抽样的步骤 简单随
机抽样系统
抽样分层
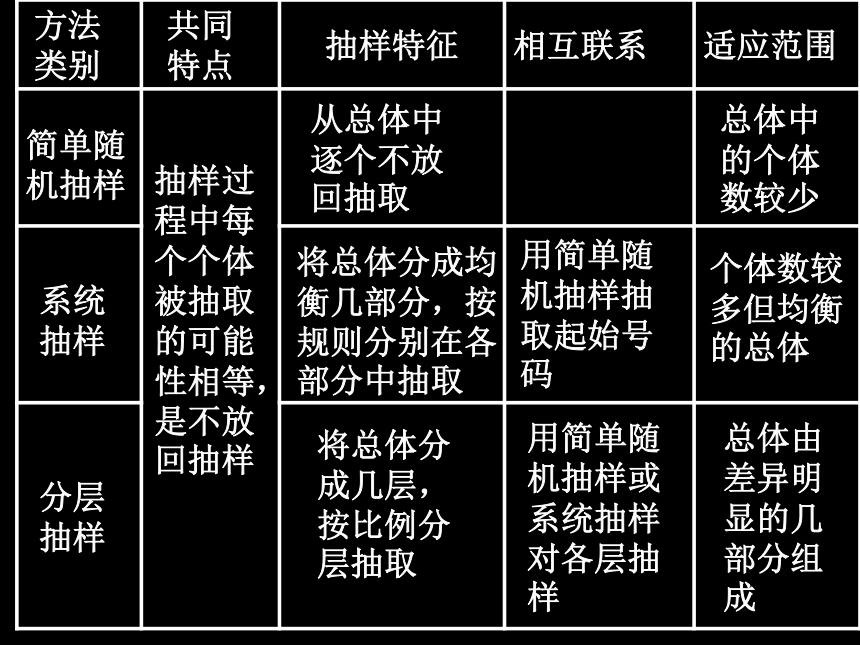
抽样抽样过程中每个个体被抽取的可能性相等,是不放回抽样将总体分成均衡几部分,按规则分别在各部分中抽取将总体分成几层,按比例分层抽取用简单随机抽样抽取起始号码总体中的个体数较少个体数较多但均衡的总体总体由差异明显的几部分组成从总体中逐个不放回抽取用简单随机抽样或系统抽样对各层抽样精讲精练1.为考查学校的教学水平,将对这个学校的高三年级的部分学生的本学年考试成绩进行考察,为了全面的反映实际情况,采取以下三种方式进行抽查(个学生都有随机编好的学号)。
(1)从全年级20个班中任意抽取一个,再从该班中任意抽取20人,考查他们的学习成绩.
(2)每个班抽取一人,共计20人考查他们的成绩。
(3)将学生按成绩分成优秀、良好、普通三个级别,从中共抽取100名学生进行考查。(其中优秀150人,良好600人,普通250人)
问题1:上面三种抽样方式中,其总体,个体,样本分别指什么?样本容量分别是多少?
问题2:请选择合适的抽样方法?
问题3: 优秀,良好 ,普通分别抽取多少人?2。在抽样过程中,每次抽取的个体不放回总体的这不放回抽样,那么分层抽样,系统抽样,简单随机抽样中,为不放回抽样的有( )个3、调查某班学生的样均身高,从50名学生抽取5名,抽样方法是( ),如果男女身高有显著不同(男生30人,女生20人),抽样方法为( ),分别抽取多少人( ),( )。P K 高考1、林场有树苗30000棵,其中松树苗4000棵,为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为( )2、初级中学共有学生2000名,各年级男、女生人数如下表:
女生男生初一年级初二年级初三年级373377370xyz已知在全校学生中随机抽取1名,抽到初二年级女生的可能性是0、19
(1)求x的值
(2)现用分层抽样的方法要全校抽取48名学生,问在初三年级抽取多少名?第二步,确定分段间隔k,对编号进行 分段.步骤:第四步,按照一定的规则抽取样本.第三步,在第1段用简单随机抽样确定起始个体编号l.第一步,将总体的所有个体编号. 2.设计科学、合理的抽样方法,其核心问题是保证抽样公平,并且样本具有好的代表性.如果要调查我校高一学生的平均身高,由于男生一般比女生高,故用简单随机抽样或系统抽样,都可能使样本不具有好的代表性.对于此类抽样问题,我们需要一个更好的抽样方法来解决.知识探究(一):分层抽样的基本思想 某地区有高中生2400人,初中生10800人,小学生11100人.当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查.分析由于样本容量与总体中的个体数的比是1:100,因此,样本中包含的各部分的个体数应该是
2400/100, 10900/100,11000/100,
即抽取24名高中生,109名初中生和110名小学生作为样本。 不同年龄阶段的学生的近视情况可能存在明显差异.因此宜将全体学生分成高中、初中和小学三部分分别抽样。另外,三部分的学生人数相差较大,因此为提高样本的代表性,还应考虑他们在样本中所占比例的大小。思考:具体在三类学生中抽取样本时(如在10800名初中生中抽取108人),可以用哪种抽样方法进行抽样?思考:在上述抽样过程中,每个学生被抽到的概率相等吗?思考:上述抽样方法不仅保证了抽样的公平性,而且抽取的样本具有较好的代表性,从而是一种科学、合理的抽样方法,这种抽样方法称为分层抽样.一般地,分层抽样的基本思想是什么? 若总体由差异明显的几部分组成,抽样时,先将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,再将各层取出的个体合在一起作为样本.知识探究(一):分层抽样的操作步骤 某单位有职工500人,其中35岁以下的有125人,35岁~49岁的有280人,50岁以上的有95人.为了调查职工的身体状况,要从中抽取一个容量为100的样本.思考1:该项调查应采用哪种抽样方法进行?思考2:按比例,三个年龄层次的职
工分别抽取多少人?35岁以下25人,35岁~49岁56人,
50岁以上19人.思考3:在各年龄段具体如何抽样?怎样获得所需样本?思考4:一般地,分层抽样的操作步骤如何?第一步,计算样本容量与总体的个体数之比.第四步,将各层抽取的个体合在一起,就得到所取样本.第三步,用简单随机抽样或系统抽样在各层中抽取相应数量的个体.第二步,将总体分成互不交叉的层,按比例确定各层要抽取的个体数.思考5:在分层抽样中,如果总体的个体数为N,样本容量为n,第i层的个体数为k,则在第i层应抽取的个体数如何计算?思考6:样本容量与总体的个体数之比是分层抽样的比例常数,按这个比例可以确定各层应抽取的个体数,如果各层应抽取的个体数不都是整数该如何处理? 调节样本容量,剔除个体. 思考7:简单随机抽样、系统抽样和分层抽样既有其共性,又有其个性,根据下表,你能对三种抽样方法作一个比较吗? 例1 某公司共有1000名员工,下设若干部门,现用分层抽样法,从全体员工中抽取一个容量为80的样本,已知策划部被抽取4个员工,求策划部的员工人数是多少?50人.理论迁移 例2 某中学有180名教职员工,其中教学人员144人,管理人员12人,后勤服务人员24人,设计一个抽样方案,从中选取15人去参观旅游.
用分层抽样,抽取教学人员12人,管理人员1人,后勤服务人员2人. 例3 某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品的销售情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务等情况,记这项调查为②,完成这两项调查宜分别采用什么方法?①用分层抽样,②用简单随机抽样.例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案. 例4 某地区中小学生人数的分布情况如下表所示(单位:人):作业:
P64习题2.1A组:5,6.
(1)从10台冰箱中抽出3台进行质量检查.
(2)从学校的10000名学生中抽取100名进行健康体检.
(3)某地区有高中生2400人,初中生10800人,小学生11100人.当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查.
问题2:总体有什么特点?
问题3:样本中高中生,初中生,小学生都必须有吗?
问题4:样本中高中生,初中生,小学生哪个人数多?分别是多少?高中生: 2400*1%=24,
初中生: 10900*1%=109,
小学生: 11000*1%=110,知识探究:分层抽样的定义分层抽样:若总体由差异明显的几部分组成,抽样时,先将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,再将各层取出的个体合在一起作为样本.
问题3:试总结分层抽样有哪些注意事项?基础探索(1)有40件产品,其中一等品有10件,二等品有25件,次品有5件,现从中抽出8件进行质量分析。
问题4:要采取何种抽样方法?
问题5:抽样比是多少?
问题6: 样品中一等品,二等品,次品分别有多少?(2)某单位有职工500人,其中35岁以下的有125人,35岁~49岁的有280人,50岁以上的有95人.为了调查职工的身体状况,要从中抽取一个容量为100的样本.试确定用何种抽样方法并写出抽样过程。问题6:试总结分层抽样的步骤 简单随
机抽样系统
抽样分层
抽样抽样过程中每个个体被抽取的可能性相等,是不放回抽样将总体分成均衡几部分,按规则分别在各部分中抽取将总体分成几层,按比例分层抽取用简单随机抽样抽取起始号码总体中的个体数较少个体数较多但均衡的总体总体由差异明显的几部分组成从总体中逐个不放回抽取用简单随机抽样或系统抽样对各层抽样精讲精练1.为考查学校的教学水平,将对这个学校的高三年级的部分学生的本学年考试成绩进行考察,为了全面的反映实际情况,采取以下三种方式进行抽查(个学生都有随机编好的学号)。
(1)从全年级20个班中任意抽取一个,再从该班中任意抽取20人,考查他们的学习成绩.
(2)每个班抽取一人,共计20人考查他们的成绩。
(3)将学生按成绩分成优秀、良好、普通三个级别,从中共抽取100名学生进行考查。(其中优秀150人,良好600人,普通250人)
问题1:上面三种抽样方式中,其总体,个体,样本分别指什么?样本容量分别是多少?
问题2:请选择合适的抽样方法?
问题3: 优秀,良好 ,普通分别抽取多少人?2。在抽样过程中,每次抽取的个体不放回总体的这不放回抽样,那么分层抽样,系统抽样,简单随机抽样中,为不放回抽样的有( )个3、调查某班学生的样均身高,从50名学生抽取5名,抽样方法是( ),如果男女身高有显著不同(男生30人,女生20人),抽样方法为( ),分别抽取多少人( ),( )。P K 高考1、林场有树苗30000棵,其中松树苗4000棵,为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为( )2、初级中学共有学生2000名,各年级男、女生人数如下表:
女生男生初一年级初二年级初三年级373377370xyz已知在全校学生中随机抽取1名,抽到初二年级女生的可能性是0、19
(1)求x的值
(2)现用分层抽样的方法要全校抽取48名学生,问在初三年级抽取多少名?第二步,确定分段间隔k,对编号进行 分段.步骤:第四步,按照一定的规则抽取样本.第三步,在第1段用简单随机抽样确定起始个体编号l.第一步,将总体的所有个体编号. 2.设计科学、合理的抽样方法,其核心问题是保证抽样公平,并且样本具有好的代表性.如果要调查我校高一学生的平均身高,由于男生一般比女生高,故用简单随机抽样或系统抽样,都可能使样本不具有好的代表性.对于此类抽样问题,我们需要一个更好的抽样方法来解决.知识探究(一):分层抽样的基本思想 某地区有高中生2400人,初中生10800人,小学生11100人.当地教育部门为了了解本地区中小学生的近视率及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查.分析由于样本容量与总体中的个体数的比是1:100,因此,样本中包含的各部分的个体数应该是
2400/100, 10900/100,11000/100,
即抽取24名高中生,109名初中生和110名小学生作为样本。 不同年龄阶段的学生的近视情况可能存在明显差异.因此宜将全体学生分成高中、初中和小学三部分分别抽样。另外,三部分的学生人数相差较大,因此为提高样本的代表性,还应考虑他们在样本中所占比例的大小。思考:具体在三类学生中抽取样本时(如在10800名初中生中抽取108人),可以用哪种抽样方法进行抽样?思考:在上述抽样过程中,每个学生被抽到的概率相等吗?思考:上述抽样方法不仅保证了抽样的公平性,而且抽取的样本具有较好的代表性,从而是一种科学、合理的抽样方法,这种抽样方法称为分层抽样.一般地,分层抽样的基本思想是什么? 若总体由差异明显的几部分组成,抽样时,先将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,再将各层取出的个体合在一起作为样本.知识探究(一):分层抽样的操作步骤 某单位有职工500人,其中35岁以下的有125人,35岁~49岁的有280人,50岁以上的有95人.为了调查职工的身体状况,要从中抽取一个容量为100的样本.思考1:该项调查应采用哪种抽样方法进行?思考2:按比例,三个年龄层次的职
工分别抽取多少人?35岁以下25人,35岁~49岁56人,
50岁以上19人.思考3:在各年龄段具体如何抽样?怎样获得所需样本?思考4:一般地,分层抽样的操作步骤如何?第一步,计算样本容量与总体的个体数之比.第四步,将各层抽取的个体合在一起,就得到所取样本.第三步,用简单随机抽样或系统抽样在各层中抽取相应数量的个体.第二步,将总体分成互不交叉的层,按比例确定各层要抽取的个体数.思考5:在分层抽样中,如果总体的个体数为N,样本容量为n,第i层的个体数为k,则在第i层应抽取的个体数如何计算?思考6:样本容量与总体的个体数之比是分层抽样的比例常数,按这个比例可以确定各层应抽取的个体数,如果各层应抽取的个体数不都是整数该如何处理? 调节样本容量,剔除个体. 思考7:简单随机抽样、系统抽样和分层抽样既有其共性,又有其个性,根据下表,你能对三种抽样方法作一个比较吗? 例1 某公司共有1000名员工,下设若干部门,现用分层抽样法,从全体员工中抽取一个容量为80的样本,已知策划部被抽取4个员工,求策划部的员工人数是多少?50人.理论迁移 例2 某中学有180名教职员工,其中教学人员144人,管理人员12人,后勤服务人员24人,设计一个抽样方案,从中选取15人去参观旅游.
用分层抽样,抽取教学人员12人,管理人员1人,后勤服务人员2人. 例3 某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品的销售情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务等情况,记这项调查为②,完成这两项调查宜分别采用什么方法?①用分层抽样,②用简单随机抽样.例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
例4 某地区中小学生人数的分布情况如下表所示(单位:人):请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.
请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案.请根据上述基本数据,设计一个样本容量为总体中个体数量的千分之一的抽样方案. 例4 某地区中小学生人数的分布情况如下表所示(单位:人):作业:
P64习题2.1A组:5,6.
