智达讲座 (储瑞年)关注热点问题 探索思维规律
文档属性
| 名称 | 智达讲座 (储瑞年)关注热点问题 探索思维规律 |  | |
| 格式 | zip | ||
| 文件大小 | 342.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-25 16:14:00 | ||
图片预览






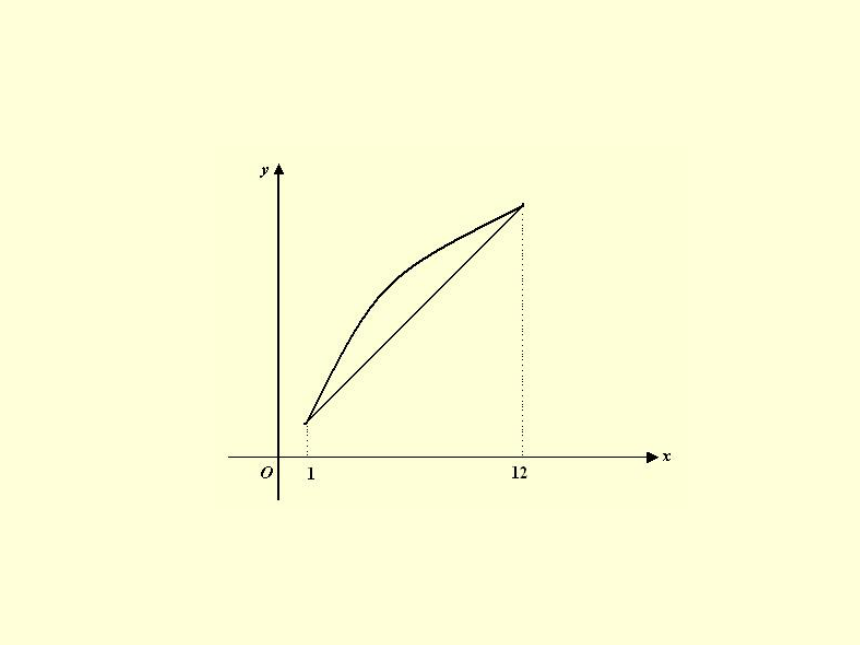
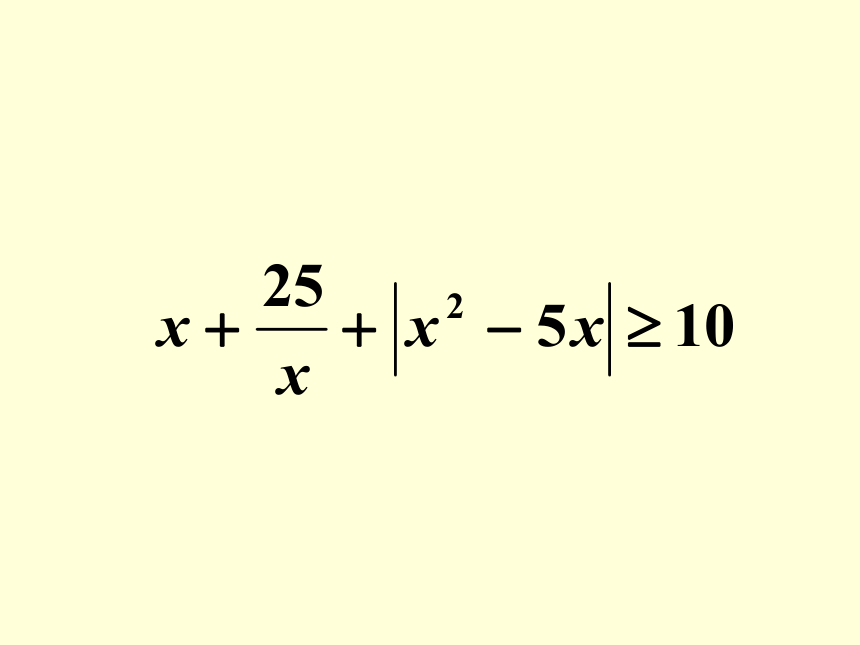




文档简介
课件87张PPT。关注热点问题
探索思维规律 2010.3.13 利德智达 数学是一门思维的科学,思维能力是数学学科能力的核心. 数学思维能力是以数学知识为素材,通过空间想象、直觉猜想、归纳抽象、符号表示、运算求解、演绎证明和模式构建等诸方面,对客观事物中的空间形式、数量关系和数学模式进行思考和判断,形成和发展理性思维,构成数学能力的主体. 一.充分性与必要性 例1 设p:f(x)=x3+2x2+mx+1 在
(-∞,+∞)内单调递增;q:m≥ , 则
p是q的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件f(x)=x3+2x2+mx+1 在(-∞,+∞)内单调递增
例2 三个同学对问题“关于x的不等式x2+25 +|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路. 甲说:“只须不等式左边的最小值不小于右边的最大值”. 乙说:“把不等式变形为左边含变量x的函 数,右边仅含常数,求函数的最值”. 丙说:“把不等式两边看成关于x的函数,作出函数图像”. 参考上述解题思路,选择你认为正确的思路,可得a的取值范围是 . ? ? ?
例3 平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行. 类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件: 充要条件① ; 充要条件② . 例4 数列{an},{bn},{cn},满足:bn=an- an+2 , cn=an+2an+1+3an+2 (n∈N*), 证明:{an}为等差数列的充分必要条件是{cn}为等差数列,且bn≤ bn+1(n∈N*) 必要性 设{an}是公差为d1的等差数列,则 bn+1-bn=(an+1-an+3)-(an-an+2) =(an+1-an)-(an+3-an+2)=d1-d1=0, 所以bn≤bn+1(n=1,2,3,…)成立, 又cn+1-cn=(an+1-an)+2(an+2-an+1)+3(an+3-an+2) =d1+2d1+3d1=6d1(常数)(n=1,2,3,…), 所以数列{cn}为等差数列.充分性 设数列{cn}是公差为d2的等差数列,且bn≤bn+1(n=1,2,3,…). ∵cn=an+2an+1+3an+2, ① ∴cn+2=an+2+2an+3+3an+4. ② ①-②得cn-cn+2=(an-an+2)+2(an+1-an+3)+3(an+2-an+4)=bn+2bn+1+3bn+2. ∵cn-cn+2=(cn-cn+1)+(cn+1-cn+2)=-2d2, ∴bn+2bn+1+3bn+2=-2d2, ③ 从而有bn+1+2bn+2+3bn+3=-2d2. ④ ④-③得(bn+1-bn)+2(bn+2-bn+1)+3(bn+3-bn+2)=0. ⑤ ∵bn+1-bn≥0,bn+2-bn+1≥0,bn+3-bn+2≥0, ∴由⑤得bn+1-bn=0 (n=1,2,3,…). 由此不妨设bn=d3(n=1,2,3,…),则 an-an+2=d3(常数). 由此cn=an+2an+1+3an+2=4an+2an+1-3d3, 从而cn+1=4an+1+2an+2-3d3=4an+1+2an-5d3. 两式相减得cn+1-cn=2(an+1-an)-2d3, 因此an+1-an=(cn+1-cn)+d3=d2+d3(常数)(n=1,2,3,…), 所以数列{an}是等差数列, 二.存在性与唯一性 例5 函数 R),区间M=[a,b](a0,a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则
的最小值为 . 函数y=loga(x+3)-1(a>0,a≠1)的图象恒过定点A(-2, -1)?-2m-n+1=0 ? 例10 过抛物线y=ax2(a>0)
的焦点F作一直线交抛物线于P,Q两点,若线段PF与FQ的长分别为p,q,则 等于 取PQ为抛物线y=ax2(a>0)的通径,则 例11 坐标原点为O,抛物线y2=2x与过焦点的直线交于A,B两点,则 = A. B. - C. 3 D. -3 抛物线y2=2x的焦点是 取AB为抛物线y2=2x的通径,则 例12 已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1. (1) 求椭圆C的标准方程; (2) 若直线l: y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标. (1)由题意设椭圆的标准方程为 ,由已知得:
a+c=3,a-c=1,解得a=2,c=1,b2=a2-c2=3,
椭圆的标准方程为 . (2)设A(x1,y1), B(x2,y2),
联立 消元,得 以AB为直径的圆过椭圆的右顶点(2,0), 四.推理与证明 例13 观察下列等式: 由以上等式推测一个一般的结论:对于n∈N*, . 3,7,11,15, …,4n-1; 1,3,5,7, …,2n-1; 例14 平面几何里有勾股定理: “设△ABC中,AB,AC互相垂直,则AB2+AC2=BC2”, 拓展到空间,类比勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC,ACD,ADB两两垂直,则 .” 已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则 等于 . 例15 设f(x)=3ax2+2bx+c, 若a+b+c=0,f(0)>0,f(1)>0,求证: (1) a>0且-2< <-1; (2) 方程f(x)=0在(0,1)内有两个实根. f(x)=3ax2+2bx+c
f(0)>0?c>0 ①
f(1)>0?3a+2b+c>0 ②
a+b+c=0 ?b=-a-c代入②,得a>c>0;
a+b+c=0 ?c=-a-b代入①,得a+b>0;
代入②,得2a+b>0;
-2< <-1 ? -2a0, a+b>0 方程f(x)=0在(0,1)内有两个实根
? 例16 等差数列{an}的前n项和为Sn,a1=1+ , S3=9+3 . (1) 求数列{an}的通项与前n项和Sn ; (2) 设 N *),求证:数列{bn}中任意不同的三项都不可能成为等比数列. (1)由已知 解得d=2,故 (2)由(1)得 .假设数列中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则 bq2 =bpbr .即 整理得(p-r)2=0,p=r.与p,q,r互不相等矛盾. 故{bn}中任意不同三项都不可能成等比数列.五.运动与变换 例17 若函数y=f(x-1)的图像与函数 的图像关于直线 y=x对称,则f(x)= A.e2x-1 B.e2x C.e2x+1 D.e2x+2 例18 正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上 的所有点在平面α内的射影构成的图形面积的取值范围是 . 当棱CD⊥平面α时,射影构成的三角形ABE面积最小,最小面积为S△ABE 当棱CD∥平面α时,射影构成的四边形AFEB面积最大,最大面积为 故正四面体上的所有点在平面内的射影构成的图形面积的取值范围是 . 例19 如图,动点P在正方体ABCD—A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方 体表面相交于M,N.设BP=x, MN=y,则函数y =f(x)的图象 大致是 例20 如图,等腰△ABC的底边 ,高CD=3,点E是线段BD上异于点B,D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE ⊥ AE,记BE=x,V(x)表示四棱锥的体积. (1) 求V(x)的表达式; (2) 当x为何值时, V(x)取得最大值? (3) 当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值. (1)由折起过程知,PE⊥平面ABC,故PE是四棱锥的高. 由EF//BC,得 六.统计与概率 例21 甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表 ? ? s1、s2、s3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有 A. s3>s1>s2 B. s2>s1>s3 C. s1>s2>s3 D. s2>s3>s1 例22 从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g): 492 496 494 495 498 497 501 502 504 496 497 503 506 508 507 492 496 500 501 499 根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5g~501.5g之间的概率约为 . 例23 对变量x, y 有观测数(xi ,yi)(i=1,2,…,10) 得散点图;对变量u ,v 有观测数据( ui , vi ) (i=1,2,…,10)得散点图. 由这两个散点图可以判断 A. 变量x 与y 正相关,u 与v 正相关 B. 变量x 与y 正相关,u 与v 负相关 C. 变量x 与y 负相关,u 与v 正相关 D. 变量x 与y 负相关,u 与v 负相关 例24 某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数). (1)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; (2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2. (i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,通过观察直方图直接回答结论) (ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).七.极值与最值 例25 若函数 在x=1处取极值,则a= . 例26 函数 的最大值为M, 最小值为m, 则 的值为 A. B. C. D. 定义域为[-3,1] 当x=-1时,函数取最大值 当x=-3或x=1时,函数取最小值m=2 例27 已知二面角α- l -β为60°, 动点P,Q分别在面α,β内,P到β的距离为 ,Q到α的距离为2 ,则P,Q两点之间距离的最小值为 A. B. 2 C. 2 D. 4 例28 如图,已知抛物线E:y2=x与圆M: 相交于A, B, C, D四点. (1) 求r的取值范围; (2) 当四边形ABCD的面 积最大时,求对角线AC, BD的交点P的坐标. 1. 联立,消元,得x2-7x+16-r2=0 ①. 抛物线E与圆M有四个交点的充要条件是方程①有 两个正根x1,x2. 2. 由Δ>0, x1+x2>0, x1x2>0,列出关于a的不等式组,解不等式组,求得r的取值范围. 3. 通过x1,x2建立表示四边形ABCD的目标函数f(t)=S2=(7+2t)2(7-2t)(0
例2 三个同学对问题“关于x的不等式x2+25 +|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路. 甲说:“只须不等式左边的最小值不小于右边的最大值”. 乙说:“把不等式变形为左边含变量x的函 数,右边仅含常数,求函数的最值”. 丙说:“把不等式两边看成关于x的函数,作出函数图像”. 参考上述解题思路,选择你认为正确的思路,可得a的取值范围是 . ? ? ?
例3 平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行. 类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件: 充要条件① ; 充要条件② . 例4 数列{an},{bn},{cn},满足:bn=an- an+2 , cn=an+2an+1+3an+2 (n∈N*), 证明:{an}为等差数列的充分必要条件是{cn}为等差数列,且bn≤ bn+1(n∈N*) 必要性 设{an}是公差为d1的等差数列,则 bn+1-bn=(an+1-an+3)-(an-an+2) =(an+1-an)-(an+3-an+2)=d1-d1=0, 所以bn≤bn+1(n=1,2,3,…)成立, 又cn+1-cn=(an+1-an)+2(an+2-an+1)+3(an+3-an+2) =d1+2d1+3d1=6d1(常数)(n=1,2,3,…), 所以数列{cn}为等差数列.充分性 设数列{cn}是公差为d2的等差数列,且bn≤bn+1(n=1,2,3,…). ∵cn=an+2an+1+3an+2, ① ∴cn+2=an+2+2an+3+3an+4. ② ①-②得cn-cn+2=(an-an+2)+2(an+1-an+3)+3(an+2-an+4)=bn+2bn+1+3bn+2. ∵cn-cn+2=(cn-cn+1)+(cn+1-cn+2)=-2d2, ∴bn+2bn+1+3bn+2=-2d2, ③ 从而有bn+1+2bn+2+3bn+3=-2d2. ④ ④-③得(bn+1-bn)+2(bn+2-bn+1)+3(bn+3-bn+2)=0. ⑤ ∵bn+1-bn≥0,bn+2-bn+1≥0,bn+3-bn+2≥0, ∴由⑤得bn+1-bn=0 (n=1,2,3,…). 由此不妨设bn=d3(n=1,2,3,…),则 an-an+2=d3(常数). 由此cn=an+2an+1+3an+2=4an+2an+1-3d3, 从而cn+1=4an+1+2an+2-3d3=4an+1+2an-5d3. 两式相减得cn+1-cn=2(an+1-an)-2d3, 因此an+1-an=(cn+1-cn)+d3=d2+d3(常数)(n=1,2,3,…), 所以数列{an}是等差数列, 二.存在性与唯一性 例5 函数 R),区间M=[a,b](a
f(0)>0?c>0 ①
f(1)>0?3a+2b+c>0 ②
a+b+c=0 ?b=-a-c代入②,得a>c>0;
a+b+c=0 ?c=-a-b代入①,得a+b>0;
代入②,得2a+b>0;
-2< <-1 ? -2a
? 例16 等差数列{an}的前n项和为Sn,a1=1+ , S3=9+3 . (1) 求数列{an}的通项与前n项和Sn ; (2) 设 N *),求证:数列{bn}中任意不同的三项都不可能成为等比数列. (1)由已知 解得d=2,故 (2)由(1)得 .假设数列中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则 bq2 =bpbr .即 整理得(p-r)2=0,p=r.与p,q,r互不相等矛盾. 故{bn}中任意不同三项都不可能成等比数列.五.运动与变换 例17 若函数y=f(x-1)的图像与函数 的图像关于直线 y=x对称,则f(x)= A.e2x-1 B.e2x C.e2x+1 D.e2x+2 例18 正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上 的所有点在平面α内的射影构成的图形面积的取值范围是 . 当棱CD⊥平面α时,射影构成的三角形ABE面积最小,最小面积为S△ABE 当棱CD∥平面α时,射影构成的四边形AFEB面积最大,最大面积为 故正四面体上的所有点在平面内的射影构成的图形面积的取值范围是 . 例19 如图,动点P在正方体ABCD—A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方 体表面相交于M,N.设BP=x, MN=y,则函数y =f(x)的图象 大致是 例20 如图,等腰△ABC的底边 ,高CD=3,点E是线段BD上异于点B,D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE ⊥ AE,记BE=x,V(x)表示四棱锥的体积. (1) 求V(x)的表达式; (2) 当x为何值时, V(x)取得最大值? (3) 当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值. (1)由折起过程知,PE⊥平面ABC,故PE是四棱锥的高. 由EF//BC,得 六.统计与概率 例21 甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表 ? ? s1、s2、s3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有 A. s3>s1>s2 B. s2>s1>s3 C. s1>s2>s3 D. s2>s3>s1 例22 从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g): 492 496 494 495 498 497 501 502 504 496 497 503 506 508 507 492 496 500 501 499 根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5g~501.5g之间的概率约为 . 例23 对变量x, y 有观测数(xi ,yi)(i=1,2,…,10) 得散点图;对变量u ,v 有观测数据( ui , vi ) (i=1,2,…,10)得散点图. 由这两个散点图可以判断 A. 变量x 与y 正相关,u 与v 正相关 B. 变量x 与y 正相关,u 与v 负相关 C. 变量x 与y 负相关,u 与v 正相关 D. 变量x 与y 负相关,u 与v 负相关 例24 某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数). (1)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; (2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2. (i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,通过观察直方图直接回答结论) (ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).七.极值与最值 例25 若函数 在x=1处取极值,则a= . 例26 函数 的最大值为M, 最小值为m, 则 的值为 A. B. C. D. 定义域为[-3,1] 当x=-1时,函数取最大值 当x=-3或x=1时,函数取最小值m=2 例27 已知二面角α- l -β为60°, 动点P,Q分别在面α,β内,P到β的距离为 ,Q到α的距离为2 ,则P,Q两点之间距离的最小值为 A. B. 2 C. 2 D. 4 例28 如图,已知抛物线E:y2=x与圆M: 相交于A, B, C, D四点. (1) 求r的取值范围; (2) 当四边形ABCD的面 积最大时,求对角线AC, BD的交点P的坐标. 1. 联立,消元,得x2-7x+16-r2=0 ①. 抛物线E与圆M有四个交点的充要条件是方程①有 两个正根x1,x2. 2. 由Δ>0, x1+x2>0, x1x2>0,列出关于a的不等式组,解不等式组,求得r的取值范围. 3. 通过x1,x2建立表示四边形ABCD的目标函数f(t)=S2=(7+2t)2(7-2t)(0
同课章节目录
