人教版九上数学24.3.1 正多边形 优质课件
文档属性
| 名称 | 人教版九上数学24.3.1 正多边形 优质课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 561.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-05 19:05:15 | ||
图片预览



文档简介
(共19张PPT)
人教版九年级上册
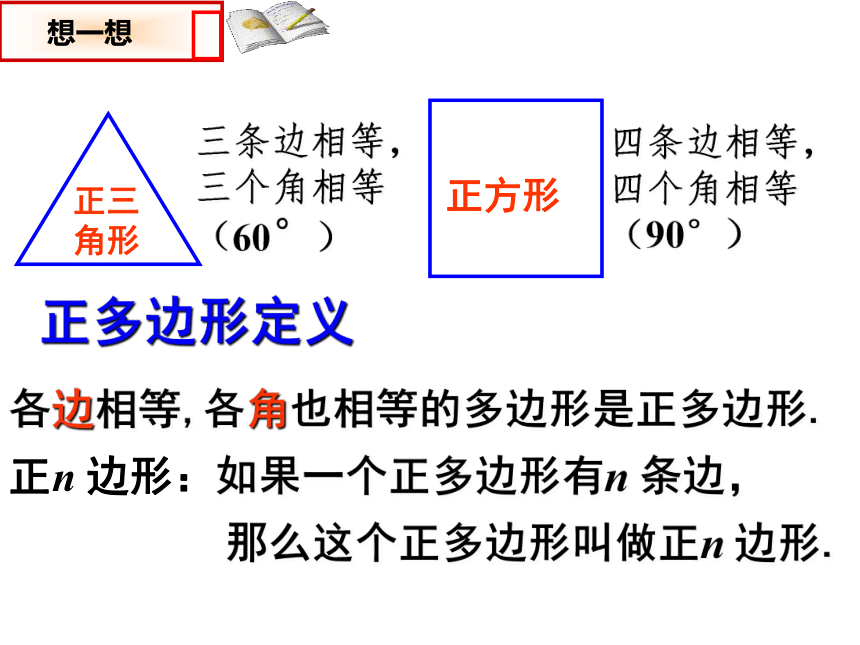
各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n 条边,
那么这个正多边形叫做正n 边形.
三条边相等,三个角相等(60°)
四条边相等,四个角相等(90°)
正三角形
正方形
正多边形定义
想一想
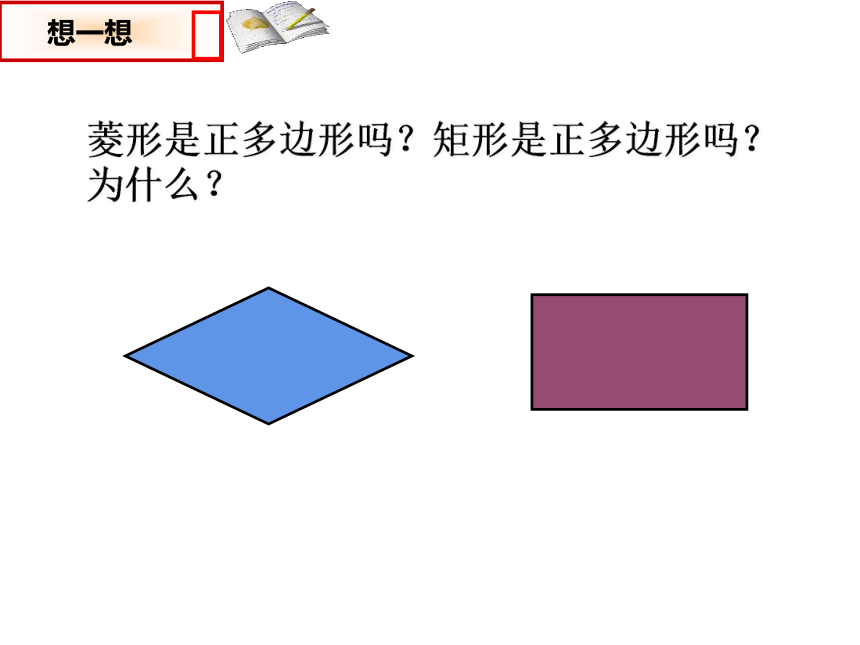
菱形是正多边形吗?矩形是正多边形吗?为什么?
想一想
正n边形的每一个内角的度数都是____________;
正多边形外角的大小是________.
同步练习
例1:已知一个正多边形的内角为 , 这个多边形是几边形?它的外角是多少?
请你们想一想有没有内角为 的正多边形呢?
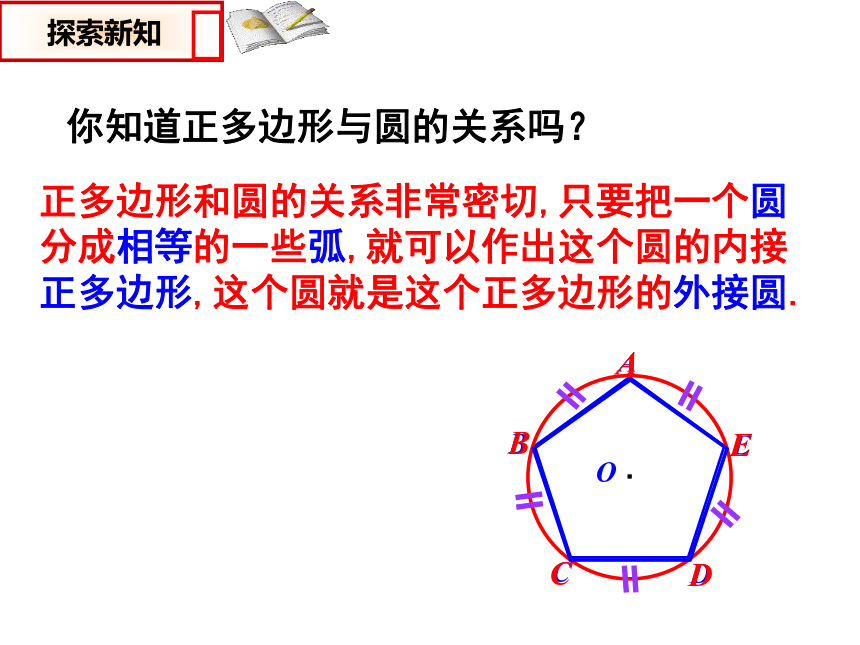
你知道正多边形与圆的关系吗?
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
·
A
B
C
D
E
O
A
B
C
D
E
探索新知
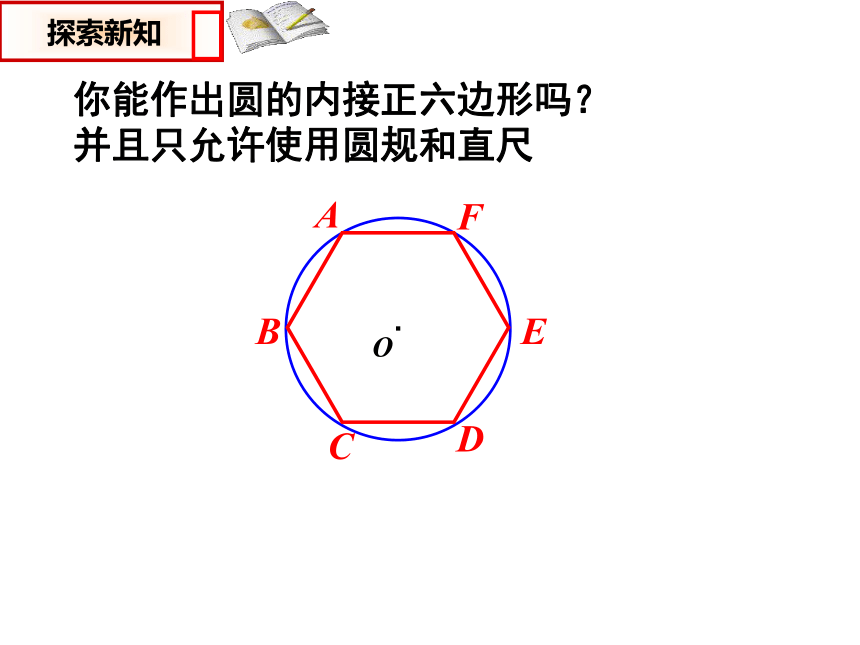
你能作出圆的内接正六边形吗?并且只允许使用圆规和直尺
探索新知
O
·
A
B
C
D
E
F
O
A
B
C
E
F
·
D
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
探索新知
③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB )
①我们把一个正多边形的外接圆(内接圆)的圆心叫做这个正多边形的中心(即点O)
②外接圆的半径叫做正多边形的半径(即OA)
④中心到正多边形的一边的距离叫做正多边形的边心距(内接圆的半径、即OM)
O
·
中心角
半径R
边心距r
A
B
C
D
E
F
M
概念学习
E
F
C
D
.
A
B
O
M
连接OC,由垂径定理(运用圆的有关知识)得
探索新知
例. 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l =4×6=24(m).
O
A
B
C
D
E
F
R
P
r
例题讲解
利用勾股定理,可得边心距
亭子地基的面积
在Rt△OPC中,OC=4, PC=
O
A
B
C
D
E
F
R
P
r
例题讲解
5.如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.
A(-1, )
B(-2,0 )
C(-1, )
D(1, )
E(2,0 )
F( 1, )
巩固练习
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。
当堂训练
边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
当堂训练
怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
120 °
①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
A
O
C
B
探索新知
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
探索新知
A
B
C
D
M
N
探索新知
1、正多边形的各边相等
2、正多边形的各角相等
课堂小结
二、正多边形的计算:
一、正多边形的性质:
三、画正多边形的方法
1.用量角器等分圆
2.尺规作图等分圆
人教版九年级上册
各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n 条边,
那么这个正多边形叫做正n 边形.
三条边相等,三个角相等(60°)
四条边相等,四个角相等(90°)
正三角形
正方形
正多边形定义
想一想
菱形是正多边形吗?矩形是正多边形吗?为什么?
想一想
正n边形的每一个内角的度数都是____________;
正多边形外角的大小是________.
同步练习
例1:已知一个正多边形的内角为 , 这个多边形是几边形?它的外角是多少?
请你们想一想有没有内角为 的正多边形呢?
你知道正多边形与圆的关系吗?
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
·
A
B
C
D
E
O
A
B
C
D
E
探索新知
你能作出圆的内接正六边形吗?并且只允许使用圆规和直尺
探索新知
O
·
A
B
C
D
E
F
O
A
B
C
E
F
·
D
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
探索新知
③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB )
①我们把一个正多边形的外接圆(内接圆)的圆心叫做这个正多边形的中心(即点O)
②外接圆的半径叫做正多边形的半径(即OA)
④中心到正多边形的一边的距离叫做正多边形的边心距(内接圆的半径、即OM)
O
·
中心角
半径R
边心距r
A
B
C
D
E
F
M
概念学习
E
F
C
D
.
A
B
O
M
连接OC,由垂径定理(运用圆的有关知识)得
探索新知
例. 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l =4×6=24(m).
O
A
B
C
D
E
F
R
P
r
例题讲解
利用勾股定理,可得边心距
亭子地基的面积
在Rt△OPC中,OC=4, PC=
O
A
B
C
D
E
F
R
P
r
例题讲解
5.如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.
A(-1, )
B(-2,0 )
C(-1, )
D(1, )
E(2,0 )
F( 1, )
巩固练习
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。
当堂训练
边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
当堂训练
怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
120 °
①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
A
O
C
B
探索新知
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
探索新知
A
B
C
D
M
N
探索新知
1、正多边形的各边相等
2、正多边形的各角相等
课堂小结
二、正多边形的计算:
一、正多边形的性质:
三、画正多边形的方法
1.用量角器等分圆
2.尺规作图等分圆
同课章节目录
