人教版八年级数学上11.2.1三角形的内角(第2课时)课件
文档属性
| 名称 | 人教版八年级数学上11.2.1三角形的内角(第2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 264.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-06 00:00:00 | ||
图片预览


文档简介
课件17张PPT。第十一章 三角形 求实中学刘晓英11.2.1 三角形的内角
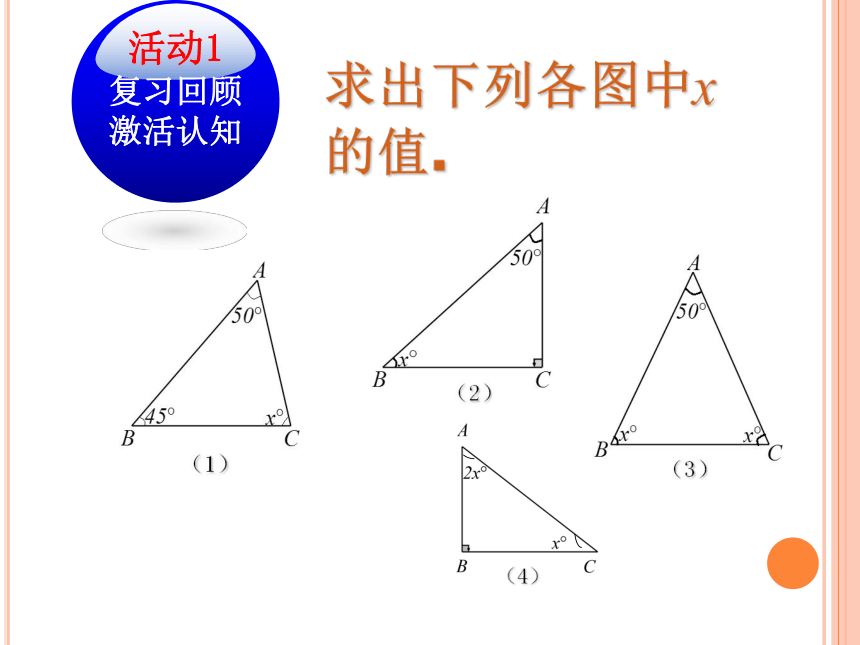
第2课时11.2 与三角形有关的角 求出下列各图中x的值.你能把下列推理补充完整吗?如图,在△ABC中,
∠A +∠B +∠C =_____( ).
∵∠C = 90°( ),
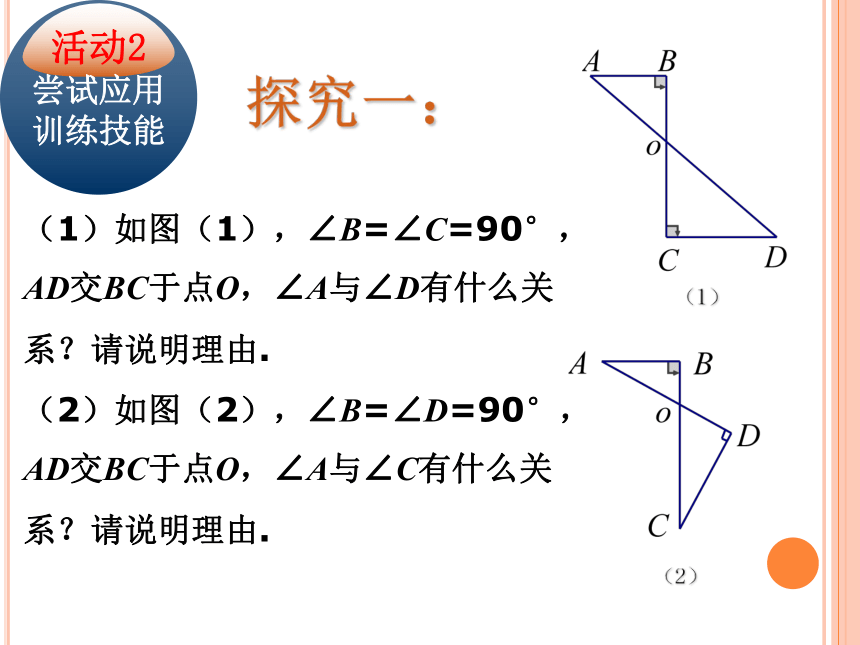
∴∠A +∠B =_______.180° 三角形内角和定理已知90°直角三角形的性质:两个锐角互余.BCA(1)如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.
(2)如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.活动2
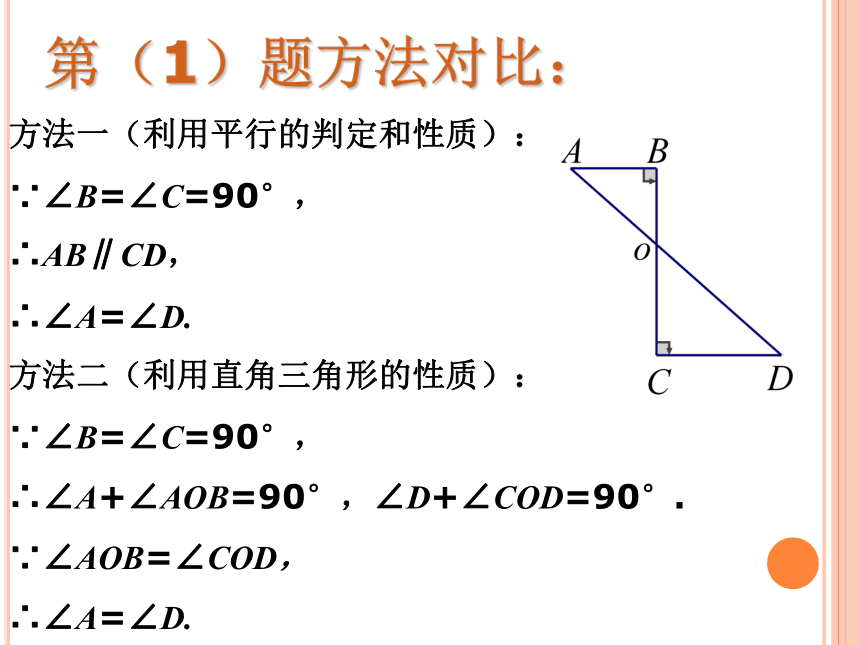
尝试应用训练技能探究一:方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
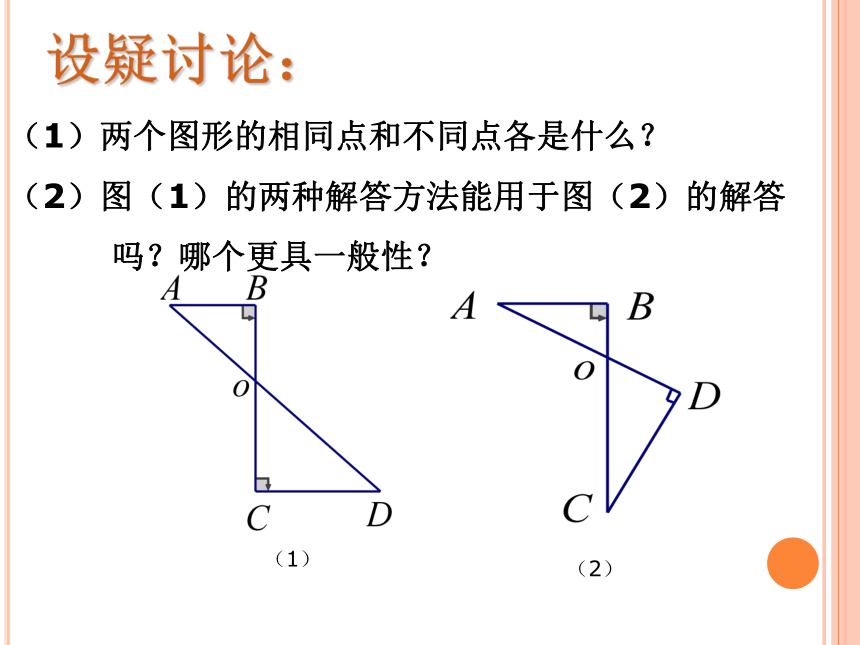
∴∠A=∠D.第(1)题方法对比:(1)两个图形的相同点和不同点各是什么?
(2)图(1)的两种解答方法能用于图(2)的解答
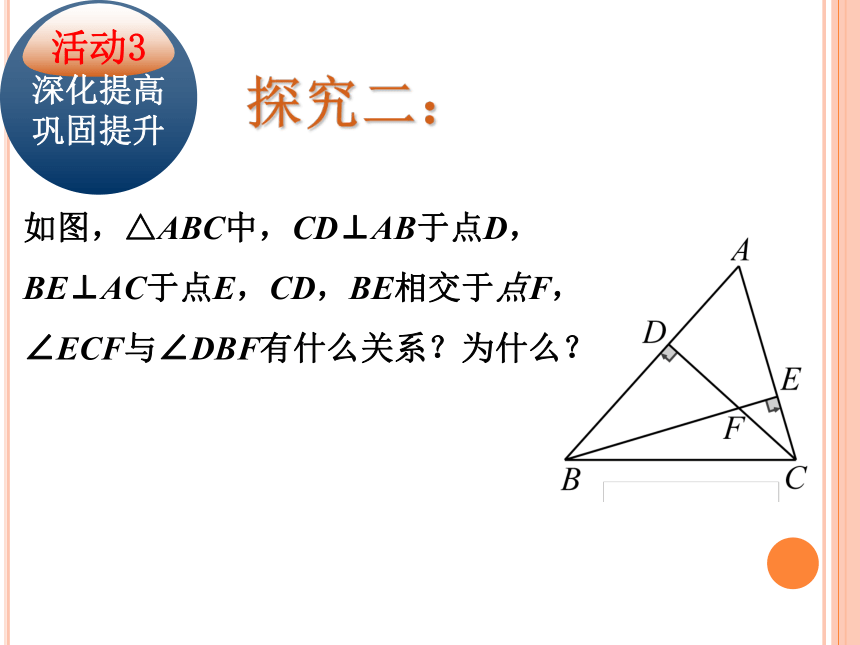
吗?哪个更具一般性?设疑讨论:如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD,BE相交于点F,∠ECF与∠DBF有什么关系?为什么?活动3
深化提高巩固提升探究二:归纳总结:你能画出不同解题方法中包含的基本图形吗?追问设疑:∠A与∠BFC又有什么关系?
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°.尝试应用: 如图,在△ABC中,∠A:∠B:∠C=3:4:5,BD、CE分别是边AC、AB上的高,BD、CE相交于H,求∠BHC的度数.活动4
正反应用回归本质思考:在△ABC中,若∠A+∠B=90°,你能判断它是什么三角形吗?请说出判断的依据. 探究三:判断:△ABC是直角三角形.
证明:∵∠A+∠B=90°,
∴∠C=180°-∠A-∠B=90°.
∴△ABC是直角三角形(直角三角形定义). 练习巩固: 1.在△ABC中,若∠A:∠B:∠C=1:2:3,那么三角形是直角三角形吗?
2.在△ABC中,若∠A+∠B=∠C,那么三角形是直角三角形吗?
思考:两个角互余是直角三角形特有的性质吗?
判定:有两个角互余的三角形是直角三角形.简单应用: 在△ABC中,若∠A=43°,∠B=47°,你能判断这是什么三角形吗?
方法一:
∵∠C=180°-∠A-∠B=180°-43°-47°=90°,
∴△ABC是直角三角形(直角三角形的定义).
方法二:
∵∠A+∠B=43°+47°=90°,
∴△ABC是直角三角形(直角三角形的判定).本节课你学习了哪些知识?活动5
课堂小结检测反馈小结与提升:直角三角形角的特征;
直角三角形的判定方法;
与直角三角形相关的几个基本图形.
活动5
归纳小结深化新知小结与提升:知识点难点知识应用小结与提升:有两个角互余的三角形是直角三角形检测反馈:教材第14页练习第1、2题.
第2课时11.2 与三角形有关的角 求出下列各图中x的值.你能把下列推理补充完整吗?如图,在△ABC中,
∠A +∠B +∠C =_____( ).
∵∠C = 90°( ),
∴∠A +∠B =_______.180° 三角形内角和定理已知90°直角三角形的性质:两个锐角互余.BCA(1)如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.
(2)如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.活动2
尝试应用训练技能探究一:方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.第(1)题方法对比:(1)两个图形的相同点和不同点各是什么?
(2)图(1)的两种解答方法能用于图(2)的解答
吗?哪个更具一般性?设疑讨论:如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD,BE相交于点F,∠ECF与∠DBF有什么关系?为什么?活动3
深化提高巩固提升探究二:归纳总结:你能画出不同解题方法中包含的基本图形吗?追问设疑:∠A与∠BFC又有什么关系?
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°.尝试应用: 如图,在△ABC中,∠A:∠B:∠C=3:4:5,BD、CE分别是边AC、AB上的高,BD、CE相交于H,求∠BHC的度数.活动4
正反应用回归本质思考:在△ABC中,若∠A+∠B=90°,你能判断它是什么三角形吗?请说出判断的依据. 探究三:判断:△ABC是直角三角形.
证明:∵∠A+∠B=90°,
∴∠C=180°-∠A-∠B=90°.
∴△ABC是直角三角形(直角三角形定义). 练习巩固: 1.在△ABC中,若∠A:∠B:∠C=1:2:3,那么三角形是直角三角形吗?
2.在△ABC中,若∠A+∠B=∠C,那么三角形是直角三角形吗?
思考:两个角互余是直角三角形特有的性质吗?
判定:有两个角互余的三角形是直角三角形.简单应用: 在△ABC中,若∠A=43°,∠B=47°,你能判断这是什么三角形吗?
方法一:
∵∠C=180°-∠A-∠B=180°-43°-47°=90°,
∴△ABC是直角三角形(直角三角形的定义).
方法二:
∵∠A+∠B=43°+47°=90°,
∴△ABC是直角三角形(直角三角形的判定).本节课你学习了哪些知识?活动5
课堂小结检测反馈小结与提升:直角三角形角的特征;
直角三角形的判定方法;
与直角三角形相关的几个基本图形.
活动5
归纳小结深化新知小结与提升:知识点难点知识应用小结与提升:有两个角互余的三角形是直角三角形检测反馈:教材第14页练习第1、2题.
