双曲线的标准方程课件
图片预览



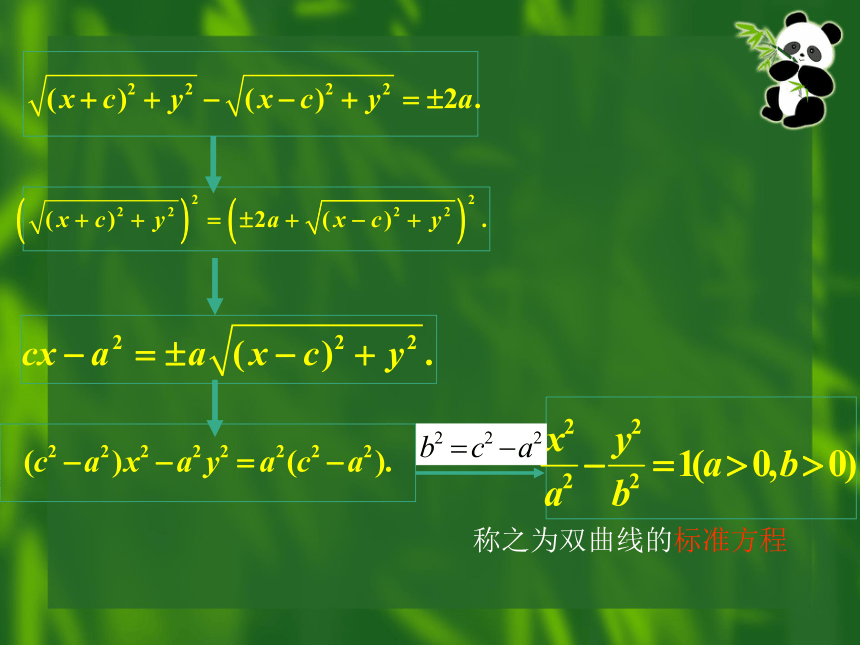

文档简介
(共26张PPT)
双曲线及其标准方程
2008.10 邳州市优质课参评课件 马洪超
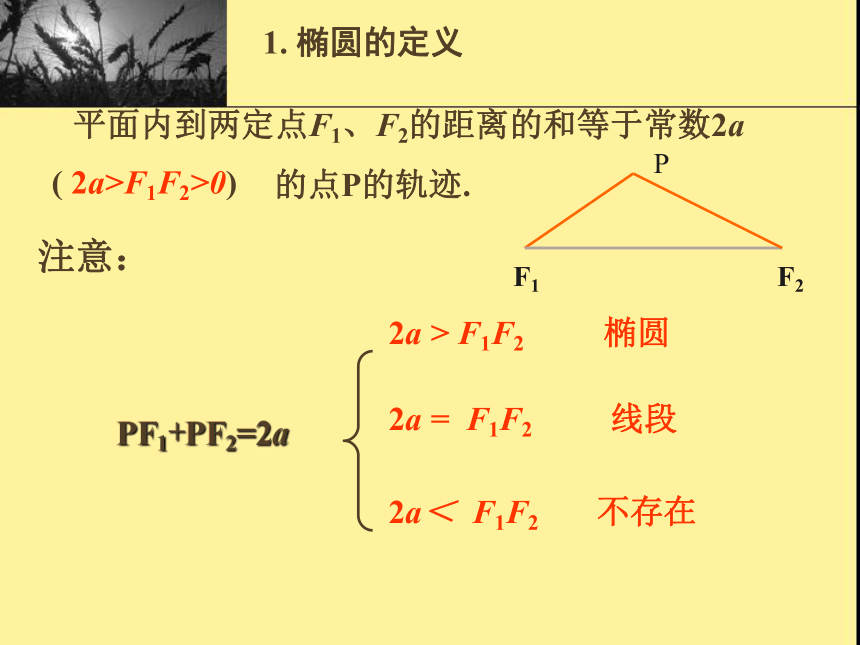
1. 椭圆的定义
平面内到两定点F1、F2的距离的和等于常数2a
的点P的轨迹.
( 2a>F1F2>0)
PF1+PF2=2a
2a > F1F2
2a = F1F2
2a< F1F2
椭圆
线段
不存在
注意:
P
F1
F2
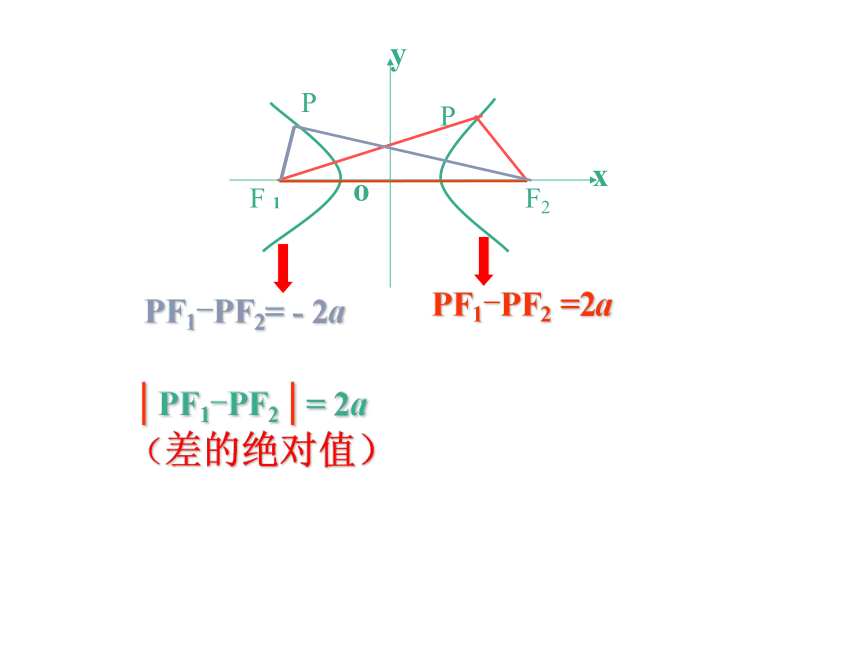
平面内到两定点F1、F2的距离的差等于常数的点的轨迹是什么呢?
思考题:
P
PF1-PF2 =2a
PF1-PF2= - 2a
| PF1-PF2 | = 2a
(差的绝对值)
o
F2
F
P
y
x
1
P
(小于F1F2的正数)
的绝对值
定义:
平面内到两个定点F1,F2的距离的差
等于常数 的点P的轨迹叫做双曲线.
焦点:定点F1、F2
焦距: F1F2=2c
若| PF1-PF2 | = 2a,则
2a < F1F2
2a=F1F2
2a> F1F2
双曲线
两条射线
不存在
P
F1
F2
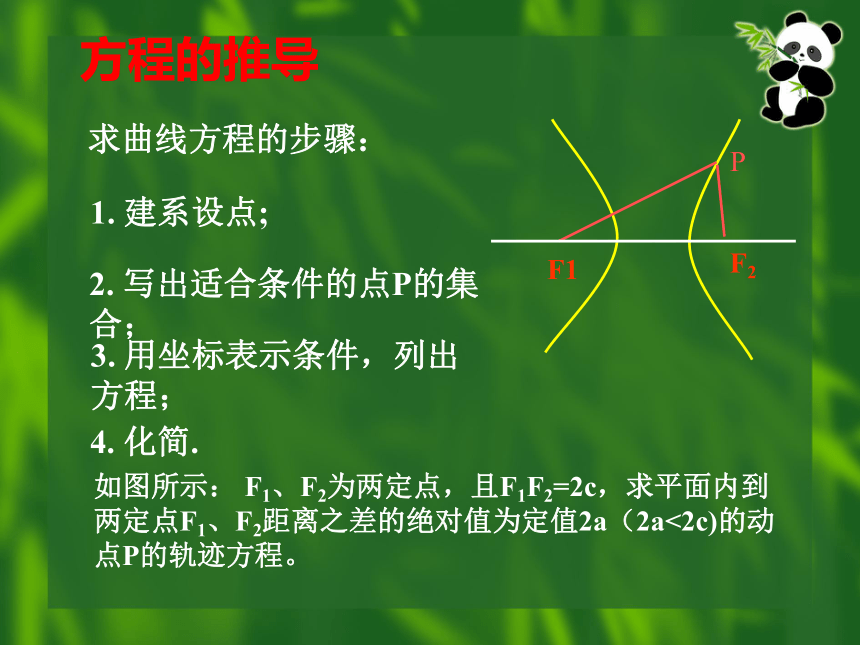
1. 建系设点;
2. 写出适合条件的点P的集合;
3. 用坐标表示条件,列出方程;
4. 化简.
求曲线方程的步骤:
方程的推导
如图所示: F1、F2为两定点,且F1F2=2c,求平面内到两定点F1、F2距离之差的绝对值为定值2a(2a<2c)的动点P的轨迹方程。
P
F2
F1
x
y
o
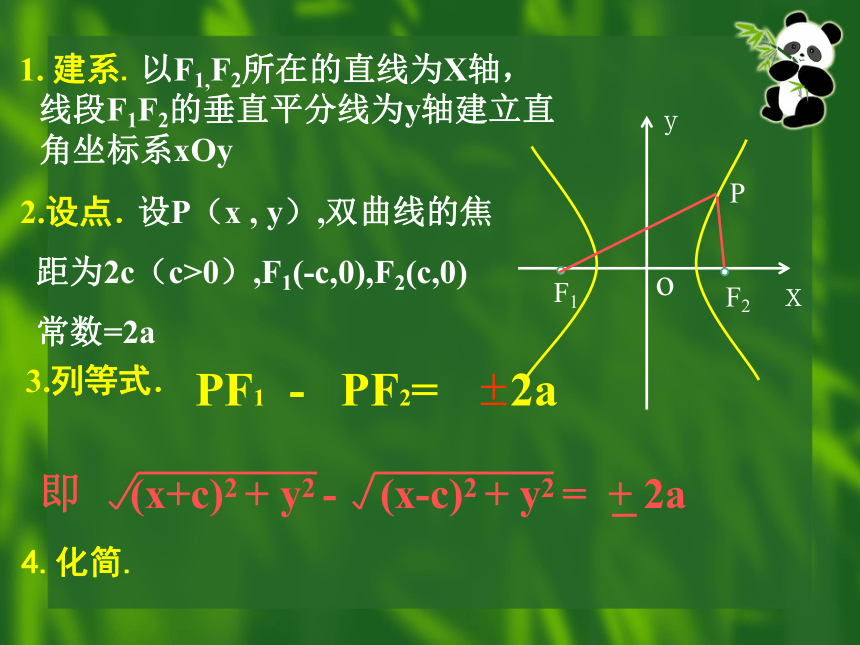
设P(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数=2a
F1
F2
P
即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a
_
以F1,F2所在的直线为X轴,线段F1F2的垂直平分线为y轴建立直角坐标系xOy
1. 建系.
2.设点.
3.列等式.
PF1 - PF2= 2a
4.化简.
称之为双曲线的标准方程
F1
F2
y
x
o
焦点在y轴上的双曲线的标准方程
想一想
F1(0,-c), F2(0,c)
图 象
方 程
焦点位置
焦点坐标 F1( )
F2( ) F1( )
F2( )
焦点在X轴
焦点在Y轴
- C , 0
C , 0
0,-C
0, C
O
P
F2
F1
x
y
F
2
F
1
P
x
O
y
确定焦 点 位置:
椭圆看分母大小
双曲看x2、y2系数正负
问题:如何判断双曲线的焦点在哪个轴上?
例1 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
∵ 2a = 6, c=5
∴ a = 3, c = 5
∴ b2 = 52-32 =16
所以所求双曲线的标准方程为:
设它的标准方程为:
解:根据题意可知,双曲线的焦点在 x 轴上,
定焦点
设方程
确定a、b、c
变题①.已知双曲线的焦点为F1(0,-5), F2(0,5),双曲线上一点P到
F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
例1 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
变题② .已知双曲线的焦点为F1(0,-5), F2(0,5),双曲线上一点P到
F1、F2的距离的差等于6,求双曲线的方程.
O
P
F2
F1
x
y
练:求适合下列条件的双曲线的标准方程。
1、
焦点在 轴上
2、焦点为
且
思考:
要求双曲线的标准
方程需要几个条件
3、
经过点
A 点在双曲线上,所以得
则
2):
设所求的曲线方程为
则有
又A 点在双曲线上,所以得
则所求的双曲线方程为
解:
1): 若所求的曲线的方程为
例2:如果方程 表示双曲线,
求m的取值范围.
分析:由
得
思考:
1 方程 表示双曲线时,则m的取值范围.
表示焦点在y轴的双曲线时,求m的范围.
2
练
2、 若方程(k2+k-2)x2+(k+1)y2=1的曲线是焦点在y轴上的
双曲线,则k .
(-1, 1)
1. 方程mx2-my2=n中mn<0,则其表示焦点在 轴上的
.
双曲线
y
3. 双曲线 的焦点坐标是 .
4. 双曲线 的焦距是6,则k= .
6
5. 若方程 表示双曲线,求实数k的
取值范围.
-25
课堂小结:
本节课学习了双曲线的定义、图象和标准方程,要注意使用类比的方法,仿照椭圆的定义、图象和标准方程的探究思路来处理双曲线的类似问题。
定义
图象
方程
焦点
a.b.c的关系
F1
F2
y
x
o
y
o
x
F1
F2
|PF1—PF2|=2a(2a<|F1F2|)
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
c2=a2+b2
双曲线
作业:
教材P39习题2.3 (1)第1,2题
思考:
1 方程 表示双曲线时,则m的取值范围.
或
表示焦点在y轴的双曲线时,求m的范围.
2
双曲线及其标准方程
2008.10 邳州市优质课参评课件 马洪超
1. 椭圆的定义
平面内到两定点F1、F2的距离的和等于常数2a
的点P的轨迹.
( 2a>F1F2>0)
PF1+PF2=2a
2a > F1F2
2a = F1F2
2a< F1F2
椭圆
线段
不存在
注意:
P
F1
F2
平面内到两定点F1、F2的距离的差等于常数的点的轨迹是什么呢?
思考题:
P
PF1-PF2 =2a
PF1-PF2= - 2a
| PF1-PF2 | = 2a
(差的绝对值)
o
F2
F
P
y
x
1
P
(小于F1F2的正数)
的绝对值
定义:
平面内到两个定点F1,F2的距离的差
等于常数 的点P的轨迹叫做双曲线.
焦点:定点F1、F2
焦距: F1F2=2c
若| PF1-PF2 | = 2a,则
2a < F1F2
2a=F1F2
2a> F1F2
双曲线
两条射线
不存在
P
F1
F2
1. 建系设点;
2. 写出适合条件的点P的集合;
3. 用坐标表示条件,列出方程;
4. 化简.
求曲线方程的步骤:
方程的推导
如图所示: F1、F2为两定点,且F1F2=2c,求平面内到两定点F1、F2距离之差的绝对值为定值2a(2a<2c)的动点P的轨迹方程。
P
F2
F1
x
y
o
设P(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数=2a
F1
F2
P
即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a
_
以F1,F2所在的直线为X轴,线段F1F2的垂直平分线为y轴建立直角坐标系xOy
1. 建系.
2.设点.
3.列等式.
PF1 - PF2= 2a
4.化简.
称之为双曲线的标准方程
F1
F2
y
x
o
焦点在y轴上的双曲线的标准方程
想一想
F1(0,-c), F2(0,c)
图 象
方 程
焦点位置
焦点坐标 F1( )
F2( ) F1( )
F2( )
焦点在X轴
焦点在Y轴
- C , 0
C , 0
0,-C
0, C
O
P
F2
F1
x
y
F
2
F
1
P
x
O
y
确定焦 点 位置:
椭圆看分母大小
双曲看x2、y2系数正负
问题:如何判断双曲线的焦点在哪个轴上?
例1 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
∵ 2a = 6, c=5
∴ a = 3, c = 5
∴ b2 = 52-32 =16
所以所求双曲线的标准方程为:
设它的标准方程为:
解:根据题意可知,双曲线的焦点在 x 轴上,
定焦点
设方程
确定a、b、c
变题①.已知双曲线的焦点为F1(0,-5), F2(0,5),双曲线上一点P到
F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
例1 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
变题② .已知双曲线的焦点为F1(0,-5), F2(0,5),双曲线上一点P到
F1、F2的距离的差等于6,求双曲线的方程.
O
P
F2
F1
x
y
练:求适合下列条件的双曲线的标准方程。
1、
焦点在 轴上
2、焦点为
且
思考:
要求双曲线的标准
方程需要几个条件
3、
经过点
A 点在双曲线上,所以得
则
2):
设所求的曲线方程为
则有
又A 点在双曲线上,所以得
则所求的双曲线方程为
解:
1): 若所求的曲线的方程为
例2:如果方程 表示双曲线,
求m的取值范围.
分析:由
得
思考:
1 方程 表示双曲线时,则m的取值范围.
表示焦点在y轴的双曲线时,求m的范围.
2
练
2、 若方程(k2+k-2)x2+(k+1)y2=1的曲线是焦点在y轴上的
双曲线,则k .
(-1, 1)
1. 方程mx2-my2=n中mn<0,则其表示焦点在 轴上的
.
双曲线
y
3. 双曲线 的焦点坐标是 .
4. 双曲线 的焦距是6,则k= .
6
5. 若方程 表示双曲线,求实数k的
取值范围.
-2
课堂小结:
本节课学习了双曲线的定义、图象和标准方程,要注意使用类比的方法,仿照椭圆的定义、图象和标准方程的探究思路来处理双曲线的类似问题。
定义
图象
方程
焦点
a.b.c的关系
F1
F2
y
x
o
y
o
x
F1
F2
|PF1—PF2|=2a(2a<|F1F2|)
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
c2=a2+b2
双曲线
作业:
教材P39习题2.3 (1)第1,2题
思考:
1 方程 表示双曲线时,则m的取值范围.
或
表示焦点在y轴的双曲线时,求m的范围.
2
