广西钦州市钦州港经济技术开发区中学2016-2017学年高一上学期新生入学考试数学试题 Word版含答案
文档属性
| 名称 | 广西钦州市钦州港经济技术开发区中学2016-2017学年高一上学期新生入学考试数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 73.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-07 21:38:03 | ||
图片预览



文档简介
高考资源网(
www.),您身边的高考专家
高考资源网(
www.),您身边的高考专家
广西钦州市钦州港经济技术开发区中学2016-2017学年高一数学
新生入学考试试题
一、
选择题
1.
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点
处,已知OA=
,AB=1,则点
的坐标是(
)
A.(
,
)
B.(
,3)
C.(
,
)
D.(
,
)
2.
在双曲线
上的点是
A.(
,
)
B.(,
)
C.(1,2)
D.(
,1)
3.
已知反比例函数
的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
A.m>0
B.m>
C.m<0
D.m<
4.
已知点(1,a)在反比例函数y=
(k≠0)的图象上,其中a=m2+2m+5(m为实数),则这个函数的图象在第_________象限.
A.一
B.二
C.一、三
D.二、四
5.
如图,A、B、C为反比例函数图像上的三个点,分别从A、B、C向x、y轴作垂线,构成三个矩形,它们的面积分别是S1、S2、S3,则S1、S2、S3的大小关系是
A:S1=S2>S3
B:S1<S2<S3
C:S1>S2>S3
D:S1=S2=S3
6.
函数
是反比例函数,则(
)
A.
m
≠0
B.
m
≠0且
m
≠1
C.
m
=2
D.
m
=1或2
7.
某水坝的坡度
i
=1∶
,坡长AB=20
m,则坝的高度为(
)
A.10
m
B.20
m
C.40
m
D.2
m
8.
sin30°的值是
(
)
A.1
B.
C.
D.
9.
若点(-2,y
1
)、(1,y
2
)、(3,y
3
)都在反比例函数y=
的图象上,则y
1
、y
2
、y
3
的大小关系是(
)
A.y
1
3
2
B.y
2
1
3
C.y
1
2
3
D.y
2
3
1
10.
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度
是体积
的反比例函数,它的图象如图3所示,当
时,气体的密度是
A.5kg/m3
B.
2kg/m
3
C
.100kg/m3
D,1kg/m3
11.
已知,在Rt△ABC中,∠C=90°,AB=
,AC=1,那么∠A的正切tan
A等于…(
)
A.
B.
2
C
.
D.
12.
计算:cos
2
45°+tan
60°cos
30°等于…(
)
A.1
B.
C.2
D.
二、
填空题
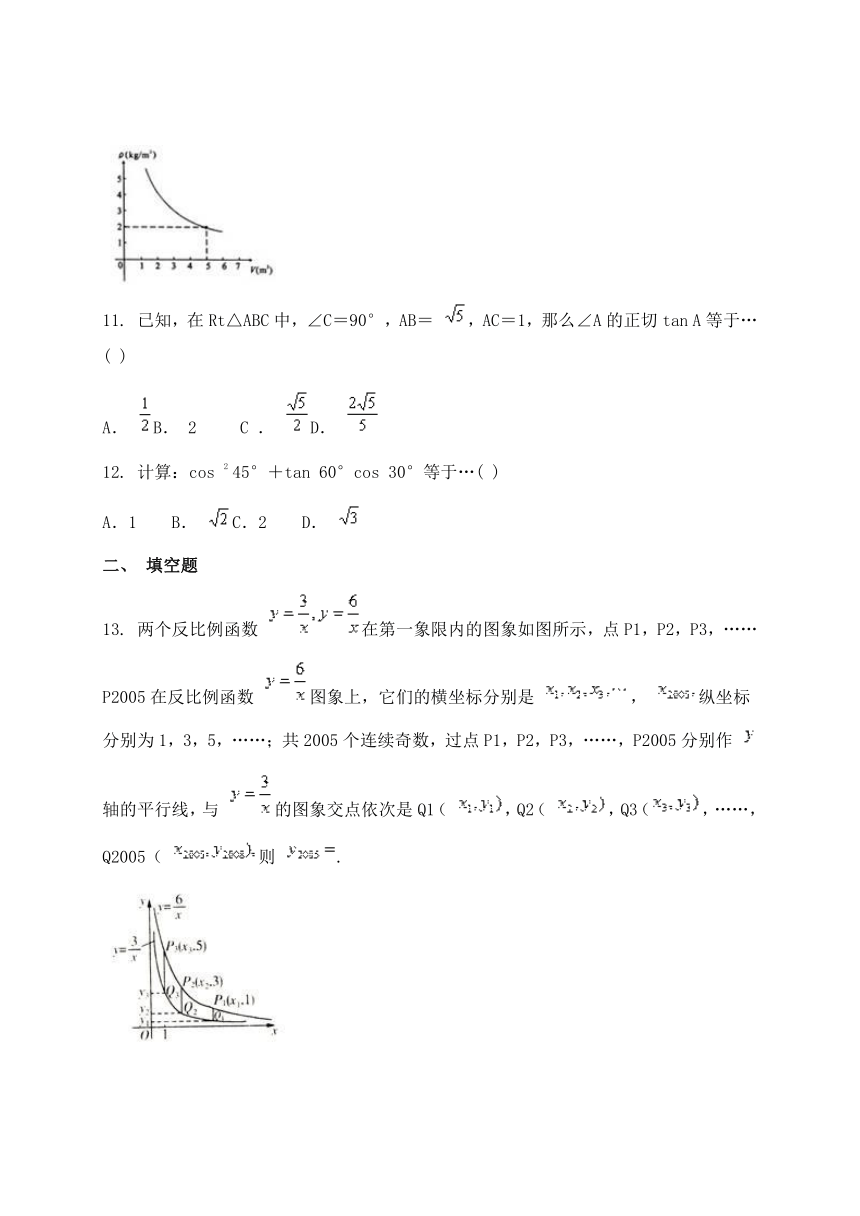
13.
两个反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数
图象上,它们的横坐标分别是
,
纵坐标分别为1,3,5,……;共2005个连续奇数,过点P1,P2,P3,……,P2005分别作
轴的平行线,与
的图象交点依次是Q1(
,Q2(
,Q3(,……,Q2005(
则
.
14.
如图,在反比例函数
y
=
(
x
>0)的图像上,有点P
1
,P
2
,P
3
,P
4
,它们的横坐标依次为1,2,3,4.分别过这些点作
x
轴与
y
轴的垂线,图中所构成的阴影部分的面积从左到右依次为S
1
,S
2
,S
3
,则S
1
+S
2
+S
3
=__________.
15.
已知两相似三角形对应高之比是12,则它们的面积之比为
.
16.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA=
.
17.
你吃过拉面吗
实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm
2
)的反比例函数,其图象如图所示.
(1)写出y与S的函数关系式:________________.
(2)当面条粗
1.6
mm
2
时,面条总长度是________________m.
三、
解答题
18.
下列函数中,哪些表示y是x的反比例函数:(1)y=
;(2)y=
;(3)xy=6;(4)3x+y=0;(5)x-2y=1;(6)3xy+2=0.
19.
小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
12.03
5.98
3.04
1.99
1.00
请你根据表格回答下列问题:
这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
请你写出这个函数的解析式。
表格中空缺的数值可能是多少?请你给出合理的数值。
20.
如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6
cm.
(1)AE的长为
cm;
(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;
(3)求点D′到BC的距离.
21.
已知Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=60°,
a
=4;
(2)
a
=
-1,
b
=3-
;
(3)∠A=60°,
c
=2+
.
22.
如图17-2-12,正比例函数y=k
1
x的图象与反比例函数y=
的图象相交于A,B两点,其中点A的坐标为(
).
图17-2-12
(1)分别写出这两个函数的表达式;
(2)你能求出点B的坐标吗
答案
一、选择题
1、
A.2、B3、D4、C5、D6、C7、A8、
D
9、
D10、D11、B12、C
二、填空题
13、
14、
15、
1:4.
16、
.
17、
(1)y=
(2)80
三、解答题
18、
(1)y=
不是反比例函数.
(2)∵y=
,∴xy=
.∴y=
,是反比例函数.
(3)∵xy=6,∴y=
,是反比例函数.
(4)∵3x+y=0,∴y=-3x,不是反比例函数.
(5)∵x-2y=1,∴2y=x-1.∴y=
x-1,不是反比例函数.
(6)∵3xy+2=0,∴xy=-
.∴y=
,是反比例函数.
19、(1)反比例函数;(2)
;(3)近似于6与4即可。
本题考查的是根据实际问题列函数关系式
根据
的乘积的特征即可得到结论。
(1)
,
,
,
,这几个计算结果都非常的接近
,故这两个变量之间可能是反比例函数关系;
(2)由(1)得
,;
(3)当
时,
;当
时,
20、
(1)
;(2)12cm;(3)
cm.
21、
解:
(1)∠A=90°-∠B=90°-60°=30°.
由tan
B=
,得
b
=
a
tan
B=4tan
60°=4
.
由cos
B=
,得
c
=
=8.
(2)由tan
B=
,得tan
B=
,
所以∠B=60°,∠A=30°.
由sin
A=
,得
c
=
.
(3)∠B=90°-∠A=90°-60°=30°.
由sin
A=
,得
a
=
c
sin
A=(2+
)sin
60°=
+
.
由cos
A=
,得
b
=
c
cos
A=(2+
)cos
60°=1+
.
22、
解:(1表达式分别为y=2x,y=
.
(2)B(
,
).
投稿兼职请联系:2355394692
www.
投稿兼职请联系:2355394692
www.
www.),您身边的高考专家
高考资源网(
www.),您身边的高考专家
广西钦州市钦州港经济技术开发区中学2016-2017学年高一数学
新生入学考试试题
一、
选择题
1.
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点
处,已知OA=
,AB=1,则点
的坐标是(
)
A.(
,
)
B.(
,3)
C.(
,
)
D.(
,
)
2.
在双曲线
上的点是
A.(
,
)
B.(,
)
C.(1,2)
D.(
,1)
3.
已知反比例函数
的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
A.m>0
B.m>
C.m<0
D.m<
4.
已知点(1,a)在反比例函数y=
(k≠0)的图象上,其中a=m2+2m+5(m为实数),则这个函数的图象在第_________象限.
A.一
B.二
C.一、三
D.二、四
5.
如图,A、B、C为反比例函数图像上的三个点,分别从A、B、C向x、y轴作垂线,构成三个矩形,它们的面积分别是S1、S2、S3,则S1、S2、S3的大小关系是
A:S1=S2>S3
B:S1<S2<S3
C:S1>S2>S3
D:S1=S2=S3
6.
函数
是反比例函数,则(
)
A.
m
≠0
B.
m
≠0且
m
≠1
C.
m
=2
D.
m
=1或2
7.
某水坝的坡度
i
=1∶
,坡长AB=20
m,则坝的高度为(
)
A.10
m
B.20
m
C.40
m
D.2
m
8.
sin30°的值是
(
)
A.1
B.
C.
D.
9.
若点(-2,y
1
)、(1,y
2
)、(3,y
3
)都在反比例函数y=
的图象上,则y
1
、y
2
、y
3
的大小关系是(
)
A.y
1
3
2
B.y
2
1
3
C.y
1
2
3
D.y
2
3
1
10.
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度
是体积
的反比例函数,它的图象如图3所示,当
时,气体的密度是
A.5kg/m3
B.
2kg/m
3
C
.100kg/m3
D,1kg/m3
11.
已知,在Rt△ABC中,∠C=90°,AB=
,AC=1,那么∠A的正切tan
A等于…(
)
A.
B.
2
C
.
D.
12.
计算:cos
2
45°+tan
60°cos
30°等于…(
)
A.1
B.
C.2
D.
二、
填空题
13.
两个反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数
图象上,它们的横坐标分别是
,
纵坐标分别为1,3,5,……;共2005个连续奇数,过点P1,P2,P3,……,P2005分别作
轴的平行线,与
的图象交点依次是Q1(
,Q2(
,Q3(,……,Q2005(
则
.
14.
如图,在反比例函数
y
=
(
x
>0)的图像上,有点P
1
,P
2
,P
3
,P
4
,它们的横坐标依次为1,2,3,4.分别过这些点作
x
轴与
y
轴的垂线,图中所构成的阴影部分的面积从左到右依次为S
1
,S
2
,S
3
,则S
1
+S
2
+S
3
=__________.
15.
已知两相似三角形对应高之比是12,则它们的面积之比为
.
16.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA=
.
17.
你吃过拉面吗
实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm
2
)的反比例函数,其图象如图所示.
(1)写出y与S的函数关系式:________________.
(2)当面条粗
1.6
mm
2
时,面条总长度是________________m.
三、
解答题
18.
下列函数中,哪些表示y是x的反比例函数:(1)y=
;(2)y=
;(3)xy=6;(4)3x+y=0;(5)x-2y=1;(6)3xy+2=0.
19.
小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
12.03
5.98
3.04
1.99
1.00
请你根据表格回答下列问题:
这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
请你写出这个函数的解析式。
表格中空缺的数值可能是多少?请你给出合理的数值。
20.
如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6
cm.
(1)AE的长为
cm;
(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;
(3)求点D′到BC的距离.
21.
已知Rt△ABC中,∠C=90°,根据下列条件解直角三角形.
(1)∠B=60°,
a
=4;
(2)
a
=
-1,
b
=3-
;
(3)∠A=60°,
c
=2+
.
22.
如图17-2-12,正比例函数y=k
1
x的图象与反比例函数y=
的图象相交于A,B两点,其中点A的坐标为(
).
图17-2-12
(1)分别写出这两个函数的表达式;
(2)你能求出点B的坐标吗
答案
一、选择题
1、
A.2、B3、D4、C5、D6、C7、A8、
D
9、
D10、D11、B12、C
二、填空题
13、
14、
15、
1:4.
16、
.
17、
(1)y=
(2)80
三、解答题
18、
(1)y=
不是反比例函数.
(2)∵y=
,∴xy=
.∴y=
,是反比例函数.
(3)∵xy=6,∴y=
,是反比例函数.
(4)∵3x+y=0,∴y=-3x,不是反比例函数.
(5)∵x-2y=1,∴2y=x-1.∴y=
x-1,不是反比例函数.
(6)∵3xy+2=0,∴xy=-
.∴y=
,是反比例函数.
19、(1)反比例函数;(2)
;(3)近似于6与4即可。
本题考查的是根据实际问题列函数关系式
根据
的乘积的特征即可得到结论。
(1)
,
,
,
,这几个计算结果都非常的接近
,故这两个变量之间可能是反比例函数关系;
(2)由(1)得
,;
(3)当
时,
;当
时,
20、
(1)
;(2)12cm;(3)
cm.
21、
解:
(1)∠A=90°-∠B=90°-60°=30°.
由tan
B=
,得
b
=
a
tan
B=4tan
60°=4
.
由cos
B=
,得
c
=
=8.
(2)由tan
B=
,得tan
B=
,
所以∠B=60°,∠A=30°.
由sin
A=
,得
c
=
.
(3)∠B=90°-∠A=90°-60°=30°.
由sin
A=
,得
a
=
c
sin
A=(2+
)sin
60°=
+
.
由cos
A=
,得
b
=
c
cos
A=(2+
)cos
60°=1+
.
22、
解:(1表达式分别为y=2x,y=
.
(2)B(
,
).
投稿兼职请联系:2355394692
www.
投稿兼职请联系:2355394692
www.
同课章节目录
