7.3 多边形及其内角和
文档属性
| 名称 | 7.3 多边形及其内角和 |

|
|
| 格式 | rar | ||
| 文件大小 | 111.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-28 00:00:00 | ||
图片预览

文档简介
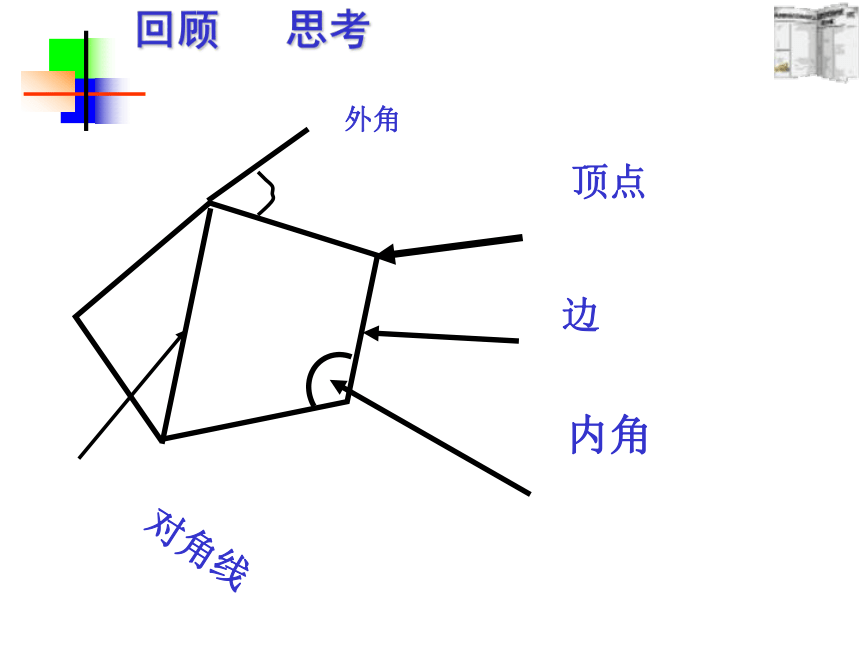
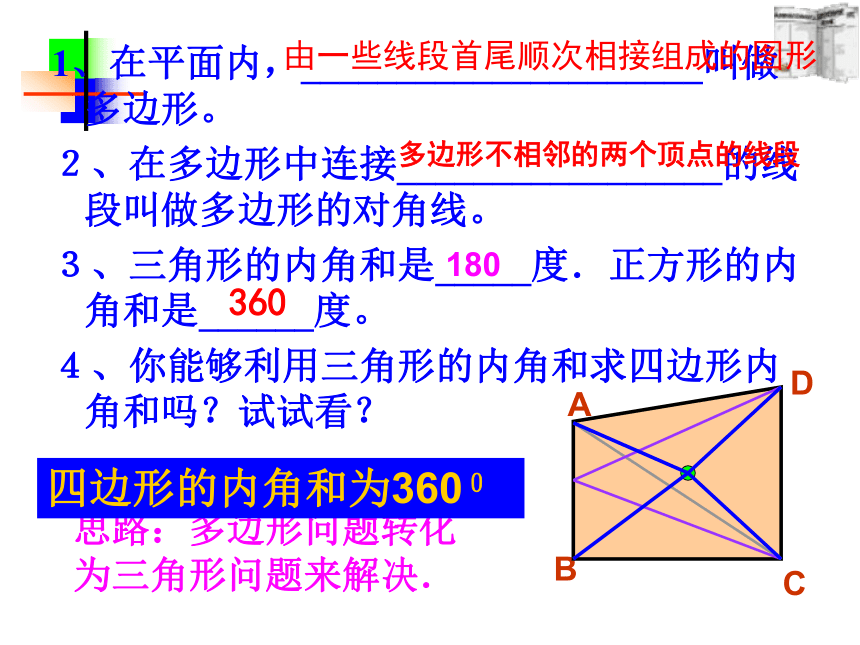
课件19张PPT。7.3.2多边形的内角和方城中学七年级备课组顶点边内角对角线回顾 思考外角1、在平面内,_____________________叫做多边形。
2、在多边形中连接_________________的线段叫做多边形的对角线。
3、三角形的内角和是_____度.正方形的内角和是______度。
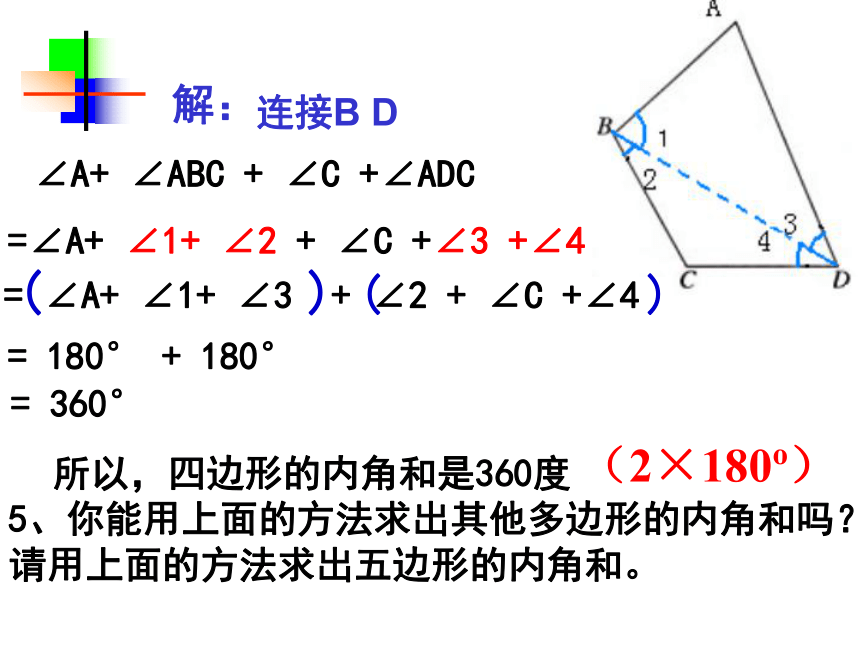
4、你能够利用三角形的内角和求四边形内角和吗?试试看?ABCD思路:多边形问题转化为三角形问题来解决.四边形的内角和为3600由一些线段首尾顺次相接组成的图形多边形不相邻的两个顶点的线段180360∠A+ ∠ABC + ∠C +∠ADC =∠A+ ∠1+ ∠2 + ∠C +∠3 +∠4 = 180° + 180° = 360° 解:
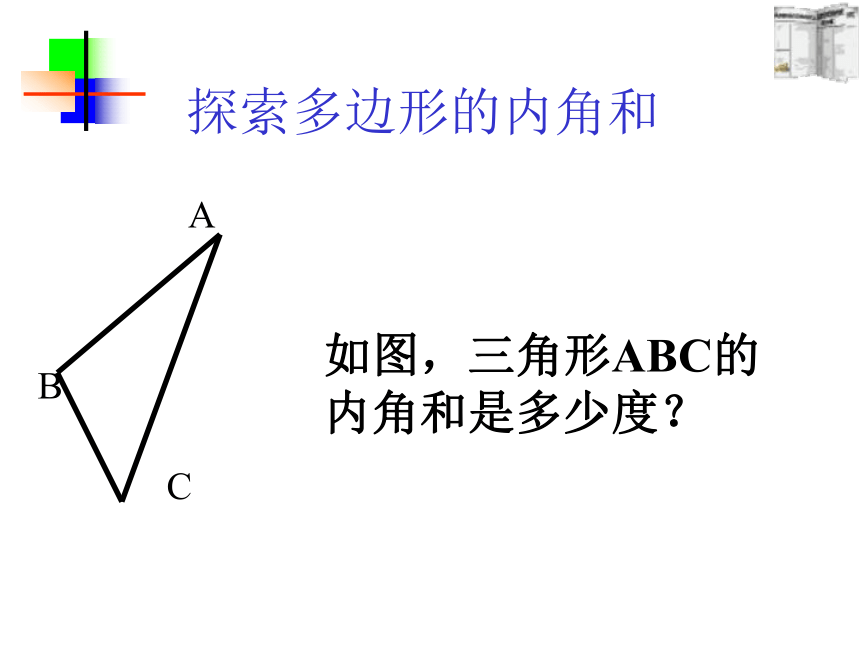
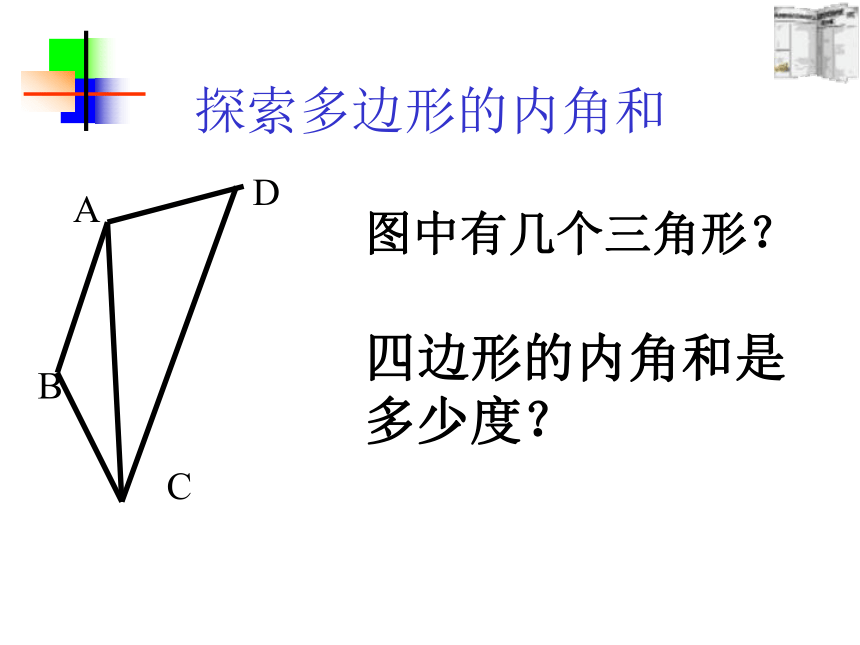
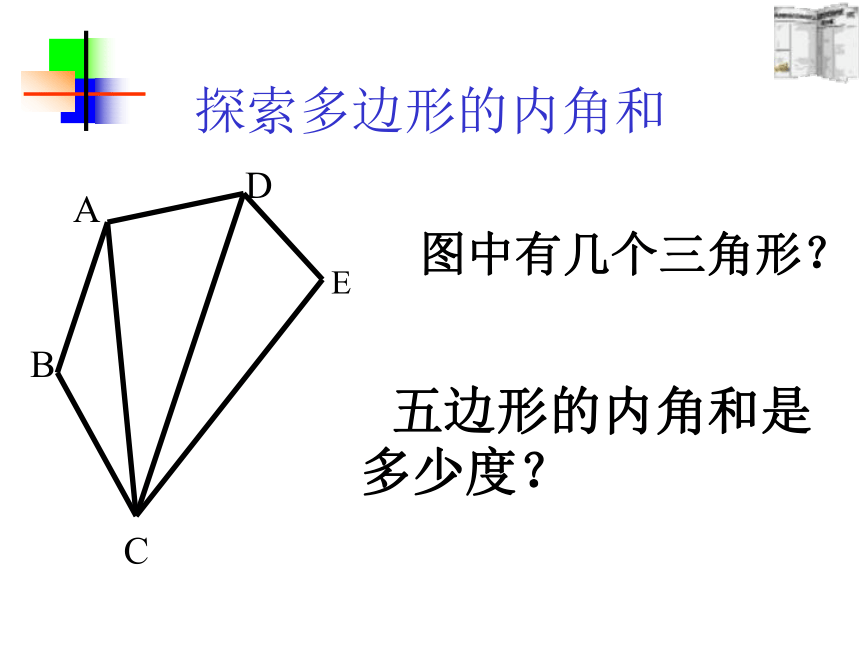
5、你能用上面的方法求出其他多边形的内角和吗?请用上面的方法求出五边形的内角和。连接B D所以,四边形的内角和是360度(2×180o)ACB如图,三角形ABC的内角和是多少度?探索多边形的内角和探索多边形的内角和ABCD四边形的内角和是多少度?图中有几个三角形?探索多边形的内角和ABDCE 五边形的内角和是多少度?图中有几个三角形?探索多边形的内角和ABDCFE六边形的内角和是多少度?图中有几个三角形?1180° 2345360° 540° 720° 900° n-2 (n-2)×180° n边形的内角和=(n-2)·180° 探索多(n)边形的内角和 多了什么?如何处理? 这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 ° 该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °多了什么?如何处理?得到定理:结 论:增加180说明:n边形的内角和等于 (n-2)·180?(1)求八边形的内角和的度数。 答:八边形的内角和为1080°。 尝试应用1(2)一多边形内角和是3240o,求它的边数。解:(n-2)×180°= 1080°=(8-2)×180 °解:设它的边数为n,由题意得(n-2) ×180=3240n-2=18n=20答:它的边数是20.应用2:(1) 有一个8边形,每个内角都相等,那么它的每个内角是多少度? 解: 8边形的内角和为 (8-2) ×180°= 1080°则它的每个内角为1080°÷8= 135°答:它的每一个内角是135°(2)一个正多边形的一个内角为150°,
你知道它是几边形吗? 解:设 这个多边形为n边形。
根据题意得:
(n-2)×180=150n
解得 n=12
答:这个多边形是12边形。 如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:
如图,四边形ABCD中,
∠A+∠C=180°∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °因为∠B+∠D= 360°-(∠A+∠C)
= 360 °-180°
=180°
所以 这就是说:如果四边形一组对角互补,那么另一组对角也互补.应用3巩固练习:3、多边形内角和为1260°则它是
( )边形。 4、多边形内角和为1800°则它是
( )边形。1、七边形内角和为( )2、十边形内角和为( )5、有一个正多边形的外角是60°,那么该正多边形是正( )边形。 900o1440o9126课堂小结
本节课你学到了哪些知识?
(2)已知内角和如何求边数;二、多边形的内角和公式的应用;一、多边形的内角和公式;
(1)已知边数如何求内角和;多边形
内角和三角形
内角和转化n边形的内角和等于(n一2)·180° .作 业:1. 习题7.3 : 4、5题
2.完成同步训练
2、在多边形中连接_________________的线段叫做多边形的对角线。
3、三角形的内角和是_____度.正方形的内角和是______度。
4、你能够利用三角形的内角和求四边形内角和吗?试试看?ABCD思路:多边形问题转化为三角形问题来解决.四边形的内角和为3600由一些线段首尾顺次相接组成的图形多边形不相邻的两个顶点的线段180360∠A+ ∠ABC + ∠C +∠ADC =∠A+ ∠1+ ∠2 + ∠C +∠3 +∠4 = 180° + 180° = 360° 解:
5、你能用上面的方法求出其他多边形的内角和吗?请用上面的方法求出五边形的内角和。连接B D所以,四边形的内角和是360度(2×180o)ACB如图,三角形ABC的内角和是多少度?探索多边形的内角和探索多边形的内角和ABCD四边形的内角和是多少度?图中有几个三角形?探索多边形的内角和ABDCE 五边形的内角和是多少度?图中有几个三角形?探索多边形的内角和ABDCFE六边形的内角和是多少度?图中有几个三角形?1180° 2345360° 540° 720° 900° n-2 (n-2)×180° n边形的内角和=(n-2)·180° 探索多(n)边形的内角和 多了什么?如何处理? 这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 ° 该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °多了什么?如何处理?得到定理:结 论:增加180说明:n边形的内角和等于 (n-2)·180?(1)求八边形的内角和的度数。 答:八边形的内角和为1080°。 尝试应用1(2)一多边形内角和是3240o,求它的边数。解:(n-2)×180°= 1080°=(8-2)×180 °解:设它的边数为n,由题意得(n-2) ×180=3240n-2=18n=20答:它的边数是20.应用2:(1) 有一个8边形,每个内角都相等,那么它的每个内角是多少度? 解: 8边形的内角和为 (8-2) ×180°= 1080°则它的每个内角为1080°÷8= 135°答:它的每一个内角是135°(2)一个正多边形的一个内角为150°,
你知道它是几边形吗? 解:设 这个多边形为n边形。
根据题意得:
(n-2)×180=150n
解得 n=12
答:这个多边形是12边形。 如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:
如图,四边形ABCD中,
∠A+∠C=180°∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °因为∠B+∠D= 360°-(∠A+∠C)
= 360 °-180°
=180°
所以 这就是说:如果四边形一组对角互补,那么另一组对角也互补.应用3巩固练习:3、多边形内角和为1260°则它是
( )边形。 4、多边形内角和为1800°则它是
( )边形。1、七边形内角和为( )2、十边形内角和为( )5、有一个正多边形的外角是60°,那么该正多边形是正( )边形。 900o1440o9126课堂小结
本节课你学到了哪些知识?
(2)已知内角和如何求边数;二、多边形的内角和公式的应用;一、多边形的内角和公式;
(1)已知边数如何求内角和;多边形
内角和三角形
内角和转化n边形的内角和等于(n一2)·180° .作 业:1. 习题7.3 : 4、5题
2.完成同步训练
