探索规律课件
图片预览


文档简介
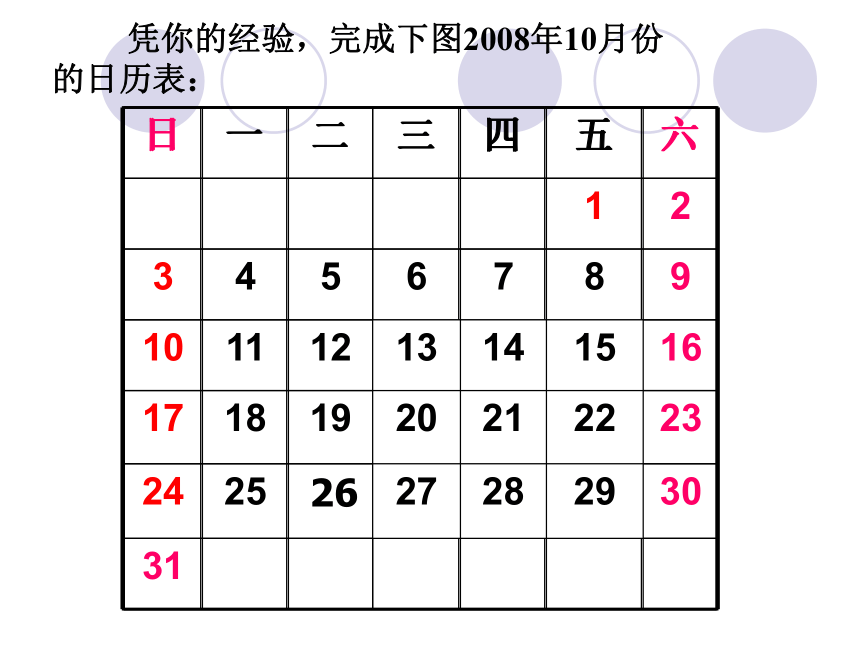
课件19张PPT。6 探索规律(一) 凭你的经验,完成下图2008年10月份的日历表:
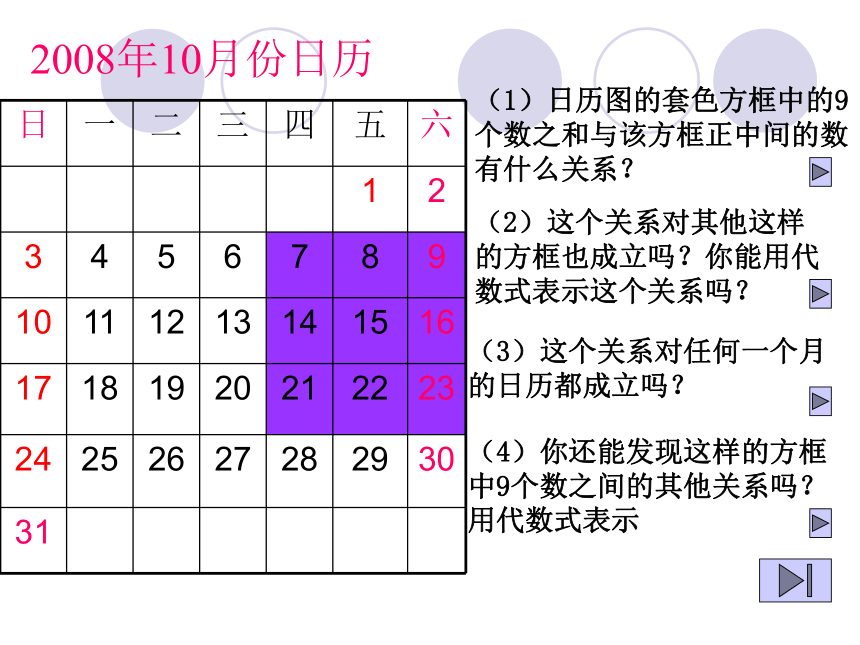
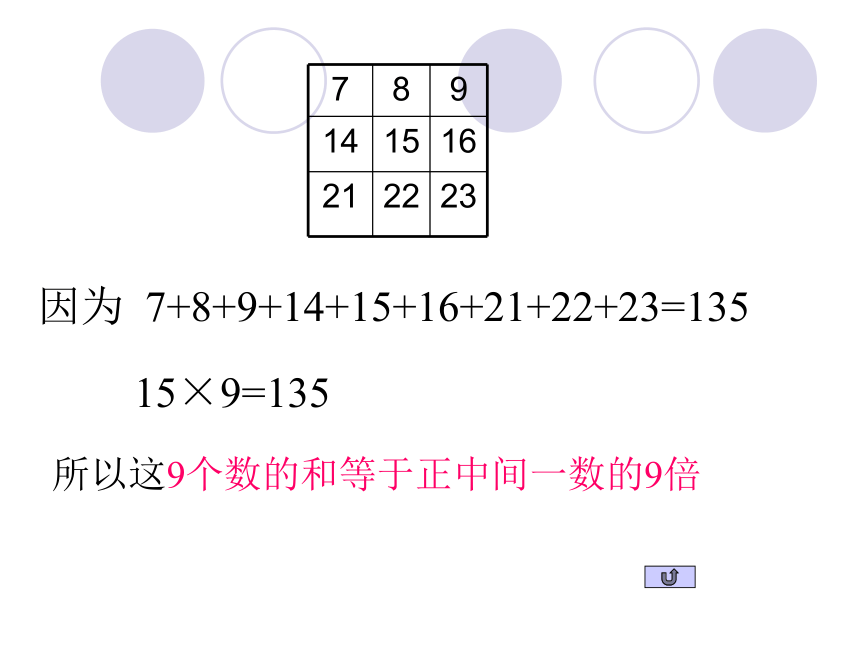
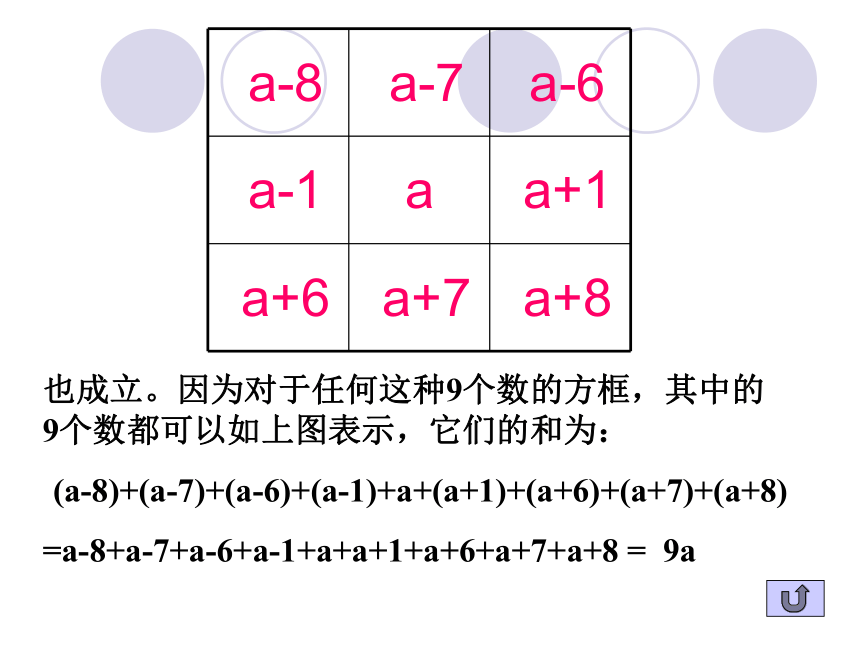
262008年10月份日历(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?(2)这个关系对其他这样的方框也成立吗?你能用代数式表示这个关系吗?(3)这个关系对任何一个月的日历都成立吗?(4)你还能发现这样的方框中9个数之间的其他关系吗?用代数式表示因为 7+8+9+14+15+16+21+22+23=135 15×9=135所以这9个数的和等于正中间一数的9倍也成立。因为对于任何这种9个数的方框,其中的9个数都可以如上图表示,它们的和为:
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)
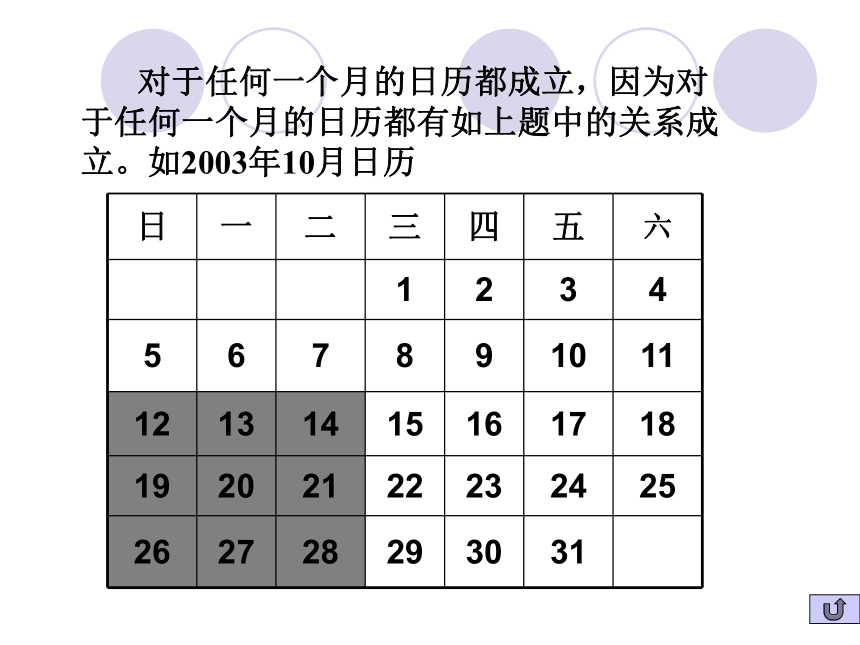
=a-8+a-7+a-6+a-1+a+a+1+a+6+a+7+a+8 = 9a 对于任何一个月的日历都成立,因为对于任何一个月的日历都有如上题中的关系成立。如2003年10月日历
还可以找到许多不同的规律,如: 1、 上图中的如 红线 所示的三数之和相等 (a-8) +a +(a+8)=(a-7) +a +(a+7)=(a-6) +a +(a+6) =(a-1) +a +(a+1) 2、紫色 线所示的三组数之和相差 21 [(a+6)+(a+7)+(a+8)]-[(a-1)+a+(a+1)]=21 [(a-1)+a+(a+1)] - [(a-8)+(a-7)+(a-6)]=21 3、黑色 线所示的三组数之和相差 3 [(a-6) +(a+1)+(a+8)]-[(a-7)+ a + (a+7)]=3 [(a-7)+ a + (a+7)]-[(a-8)+ (a-1)+(a+6)]=31.在如图所示的两个方框或其它多种方框中,一条对角线上两数的和等于另一条对角线上两数的和.
不断探索,余味无穷2、在十字形的区域中,五个数字的和等于正中心数
的5倍。
若设中心数为a, 则这五个数之和为:
(a-7)+(a+7)+(a-1)+(a+1)+a=5a
3.在 H 形区域中,7个数的和等于正中心数的7倍.
若设中心数为a, 则这七个数之和为:
(a-8)+(a-1)+(a+6)+a+(a- 6)+(a+1)+(a+8)=7a
4. 在w形区域中,七个数的和等于中心数的7倍.
若设中心数为a,则这七个数之和为:
(a-10)+(a-2)+(a+6)+(a+8)+(a+2)+(a-4)+a=7a
相信你一定行 用火柴棒按下图的方式搭三角形 (2)照这样的规律搭下去,搭n个这样的三角形
需要多少根火柴棒?(1)填写下表:搭n个这样的三角形需要 2n+1 根火柴棒 3 11 9 5 7细胞分裂问题细胞每次都是由一个分裂成两个。24816212223242n…我们曾经接触过“细胞分裂”问题:思路启迪 ? 可从具体的、简单的对折次数入手,寻找 所得折痕数与对折次数的变化关系. 13715…24816…212223242n2n-1 将一张长方形的纸对折,如右图所示可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折n次后,可以得到多少条折痕?折 纸 问 题谁能算出:1+2+22+23+24+……2n=?
13715…24816…212223242n2n-1观察上表可得: 1=21- 1 3=1+ 21 =22- 1
7=1+21 +22 =23- 1
15= 1+21 +22 +23=24- 1……所以 1+2+22+23+24+……2n=
2n+1-1+2+4+8 开学初,谢峥同学曾有一次惊喜地告诉我,他发现了一个规律:1×3= 22 –1 , 2×4= 32 –1 , 3×5= 42 –1 , …你看出这个规律了吗?试试看,你能利用这个规律口算出下面结果吗?24 ×26=?79 ×81=?你还能用数学语言表示出这种规律吗?
善于探索,体验成功(n-1)(n+1)= n2 -124 ×26= 252 –1=624, 79 ×81= 802 –1=6399 探索规律的一般步骤:猜 想 规 律表 示 规 律验 证 规 律具 体 问 题观 察 特 例成立得出结论头 回新 重索 探
1、 作业纸:探索规律(一)
2、挑战自我:1+3+32+ 33 +34+…+ 3n=?
(先自主探究,实在困难时小组合作能解决也算非常不错了。)
3、出题比赛:每个合作小组共同设计一个探索规律题(不得抄袭),截止本周五上交评奖。动手实践 谢谢各位莅临指导
欢迎多提宝贵意见
再见
262008年10月份日历(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系?(2)这个关系对其他这样的方框也成立吗?你能用代数式表示这个关系吗?(3)这个关系对任何一个月的日历都成立吗?(4)你还能发现这样的方框中9个数之间的其他关系吗?用代数式表示因为 7+8+9+14+15+16+21+22+23=135 15×9=135所以这9个数的和等于正中间一数的9倍也成立。因为对于任何这种9个数的方框,其中的9个数都可以如上图表示,它们的和为:
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)
=a-8+a-7+a-6+a-1+a+a+1+a+6+a+7+a+8 = 9a 对于任何一个月的日历都成立,因为对于任何一个月的日历都有如上题中的关系成立。如2003年10月日历
还可以找到许多不同的规律,如: 1、 上图中的如 红线 所示的三数之和相等 (a-8) +a +(a+8)=(a-7) +a +(a+7)=(a-6) +a +(a+6) =(a-1) +a +(a+1) 2、紫色 线所示的三组数之和相差 21 [(a+6)+(a+7)+(a+8)]-[(a-1)+a+(a+1)]=21 [(a-1)+a+(a+1)] - [(a-8)+(a-7)+(a-6)]=21 3、黑色 线所示的三组数之和相差 3 [(a-6) +(a+1)+(a+8)]-[(a-7)+ a + (a+7)]=3 [(a-7)+ a + (a+7)]-[(a-8)+ (a-1)+(a+6)]=31.在如图所示的两个方框或其它多种方框中,一条对角线上两数的和等于另一条对角线上两数的和.
不断探索,余味无穷2、在十字形的区域中,五个数字的和等于正中心数
的5倍。
若设中心数为a, 则这五个数之和为:
(a-7)+(a+7)+(a-1)+(a+1)+a=5a
3.在 H 形区域中,7个数的和等于正中心数的7倍.
若设中心数为a, 则这七个数之和为:
(a-8)+(a-1)+(a+6)+a+(a- 6)+(a+1)+(a+8)=7a
4. 在w形区域中,七个数的和等于中心数的7倍.
若设中心数为a,则这七个数之和为:
(a-10)+(a-2)+(a+6)+(a+8)+(a+2)+(a-4)+a=7a
相信你一定行 用火柴棒按下图的方式搭三角形 (2)照这样的规律搭下去,搭n个这样的三角形
需要多少根火柴棒?(1)填写下表:搭n个这样的三角形需要 2n+1 根火柴棒 3 11 9 5 7细胞分裂问题细胞每次都是由一个分裂成两个。24816212223242n…我们曾经接触过“细胞分裂”问题:思路启迪 ? 可从具体的、简单的对折次数入手,寻找 所得折痕数与对折次数的变化关系. 13715…24816…212223242n2n-1 将一张长方形的纸对折,如右图所示可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折n次后,可以得到多少条折痕?折 纸 问 题谁能算出:1+2+22+23+24+……2n=?
13715…24816…212223242n2n-1观察上表可得: 1=21- 1 3=1+ 21 =22- 1
7=1+21 +22 =23- 1
15= 1+21 +22 +23=24- 1……所以 1+2+22+23+24+……2n=
2n+1-1+2+4+8 开学初,谢峥同学曾有一次惊喜地告诉我,他发现了一个规律:1×3= 22 –1 , 2×4= 32 –1 , 3×5= 42 –1 , …你看出这个规律了吗?试试看,你能利用这个规律口算出下面结果吗?24 ×26=?79 ×81=?你还能用数学语言表示出这种规律吗?
善于探索,体验成功(n-1)(n+1)= n2 -124 ×26= 252 –1=624, 79 ×81= 802 –1=6399 探索规律的一般步骤:猜 想 规 律表 示 规 律验 证 规 律具 体 问 题观 察 特 例成立得出结论头 回新 重索 探
1、 作业纸:探索规律(一)
2、挑战自我:1+3+32+ 33 +34+…+ 3n=?
(先自主探究,实在困难时小组合作能解决也算非常不错了。)
3、出题比赛:每个合作小组共同设计一个探索规律题(不得抄袭),截止本周五上交评奖。动手实践 谢谢各位莅临指导
欢迎多提宝贵意见
再见
