勾股定理逆定理学案(全章都有)
文档属性
| 名称 | 勾股定理逆定理学案(全章都有) |

|
|
| 格式 | rar | ||
| 文件大小 | 40.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-29 00:00:00 | ||
图片预览


文档简介
18.1勾股定理(一)
主备 人:李善国
学习目标
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
3.了解我国古代在勾股定理研究方面所取得的成就,激发爱国热情。
重点、难点
1.重点:勾股定理的内容及证明。
2.难点:勾股定理的证明。
学习过程:
1. 自主探究
(1) 画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出斜边AB的长。
(2) 再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长。
你是否发现32+42与52的关系,52+122和132的关系,即 。
对于任意的直角三角形也有这个性质吗?人们把这个性质叫做 。
已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证:a2+b2=c2。
小组成员相互合作,找出不同的证法。
结论:
二.合作交流 1。小组内交流 2。组间交流 3。师生共同归纳
三.展示应用
1.在Rt△ABC,∠C=90°
⑴已知a=b=5,求c。
⑵已知a=1,c=2, 求b。
⑶已知c=17,b=8, 求a。
(4)已知b=15,∠A=30°,求a,c。
2.已知直角三角形的两边长分别为5和12,求第三边。
3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
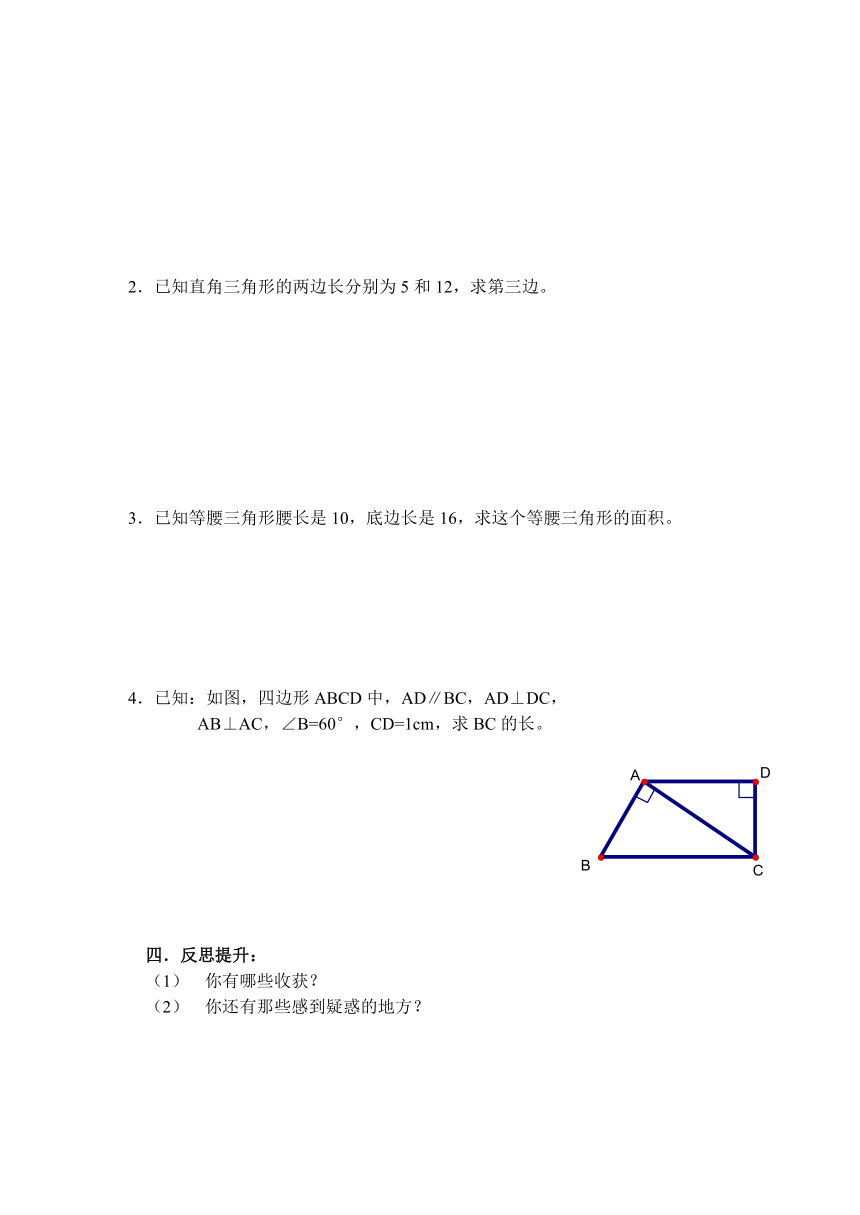
4.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,
AB⊥AC,∠B=60°,CD=1cm,求BC的长。
四.反思提升:
(1) 你有哪些收获?
(2) 你还有那些感到疑惑的地方?
18.1 勾股定理(二)
主备人:李善国
学习目标
1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
学习重点、难点
1.重点:勾股定理的应用。
2.难点:实际问题向数学问题的转化。
学习过程:
1. 自主探究:
勾股定理在实际的生产生活当中有着广泛的应用。勾股定理的发现和使用解决了许多生活中的问题,今天我们就来运用勾股定理解决一些问题,你可以吗?试一试。
1.教材P74页探究1
二.合作交流 1。组内交流 2。组间交流 3。师生共同归纳
三.展示应用
1. 教材P75页探究2
2.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
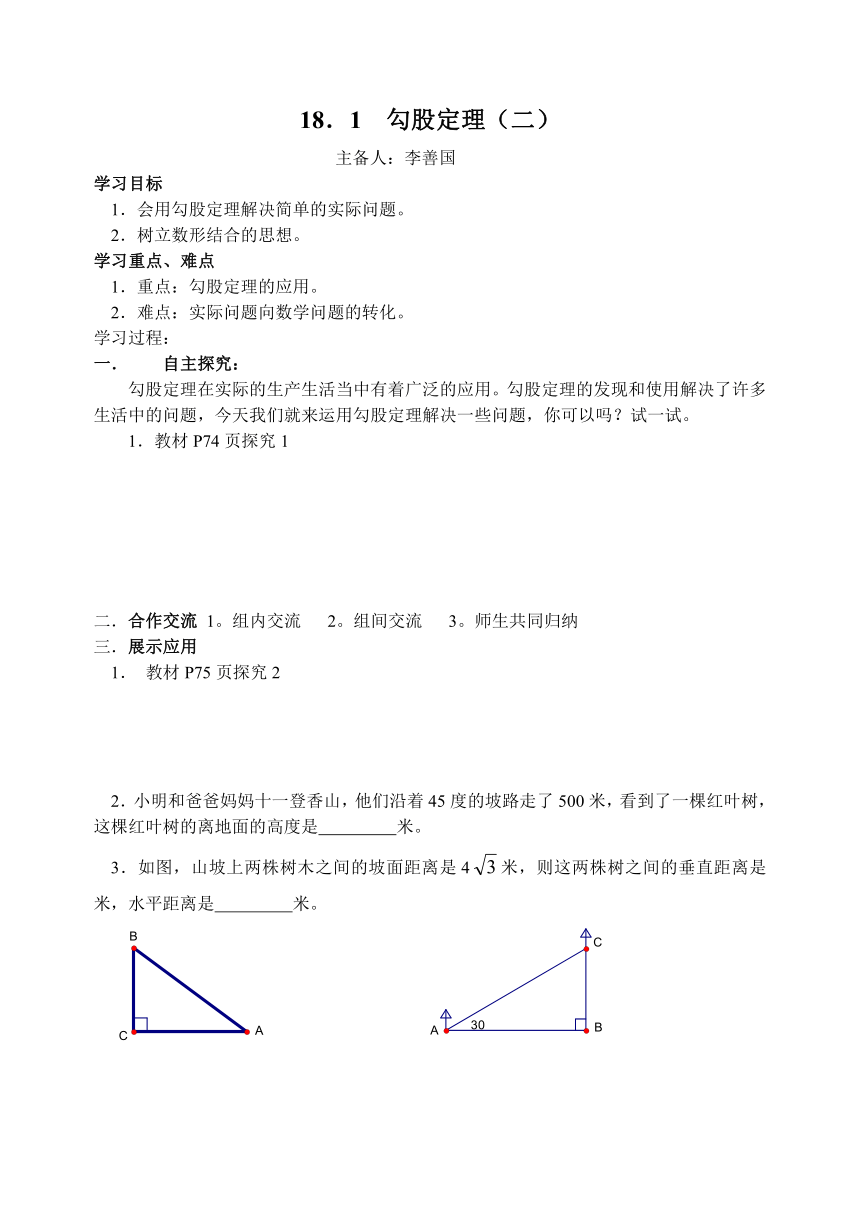
3.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是 米,水平距离是 米。
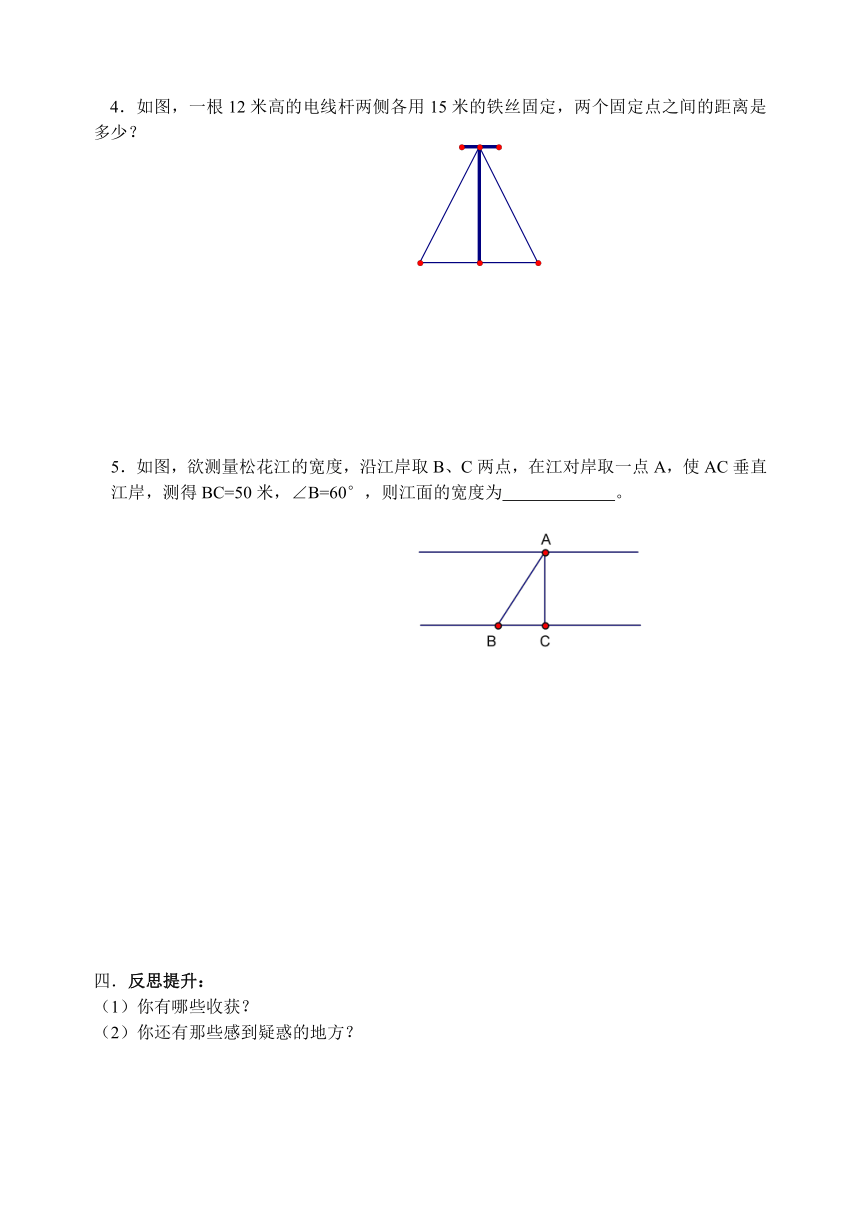
4.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是多少?
5.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为 。
四.反思提升:
(1)你有哪些收获?
(2)你还有那些感到疑惑的地方?
18.2 勾股定理的逆定理(一)
主备人:李善国
学习目标
1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.探究勾股定理的逆定理的证明方法。
3.理解原命题、逆命题、逆定理的概念及关系。
学习重点、难点
1.重点:掌握勾股定理的逆定理及证明。
2.难点:勾股定理的逆定理的证明。
学习过程:
1. 自主探究
(一)复习
1. ⑴怎样判定一个三角形是等腰三角形?
⑵怎样判定一个三角形是直角三角形?和等腰三角形的判定进行对比,从勾股定理的逆命题进行猜想。
2.说出下列命题的逆命题,这些命题的逆命题成立吗?
⑴同旁内角互补,两条直线平行。
⑵如果两个实数的平方相等,那么两个实数平方相等。
⑶线段垂直平分线上的点到线段两端点的距离相等。
⑷直角三角形中30°角所对的直角边等于斜边的一半。
(二)自学
1.例(P82探究)
证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
2. 合作交流 1。组内交流 2。组间交流 3。师生共同归纳
三。展示应用
1.下列四条线段不能组成直角三角形的是( )
A.a=8,b=15,c=17
B.a=9,b=12,c=15
C.a=,b=,c=
D.a:b:c=2:3:4
2.叙述下列命题的逆命题,并判断逆命题是否正确。
⑴如果a3>0,那么a2>0;
⑵如果三角形有一个角小于90°,那么这个三角形是锐角三角形;
⑶如果两个三角形全等,那么它们的对应角相等;
⑷关于某条直线对称的两条线段一定相等。
3.填空题。
⑴任何一个命题都有 ,但任何一个定理未必都有 。
⑵“两直线平行,内错角相等。”的逆定理是 。
⑶在△ABC中,若a2=b2-c2,则△ABC是 三角形, 是直角;若a2<b2-c2,则∠B是 。
⑷若在△ABC中,a=m2-n2,b=2mn,c= m2+n2,则△ABC是 三角形。
4.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?
⑴a=9,b=41,c=40;
(2)a=5k,b=12k,c=13k(k>0)。
四.反思提升:
(3) 你有哪些收获?
(4) 你还有那些感到疑惑的地方?
18.2 勾股定理的逆定理(二)
主备人:李善国
学习目标
1.灵活应用勾股定理及逆定理解决实际问题。
2.进一步加深性质定理与判定定理之间关系的认识。
学习重点、难点
1.重点:灵活应用勾股定理及逆定理解决实际问题。
2.难点:灵活应用勾股定理及逆定理解决实际问题。
学习过程:
1. 自主探究
1.(P83例2)
2.一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
2. 合作交流
1. 组内交流
2。组间交流 3。师生共同归纳
3. 展示应用
1.△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形。
B.如果c2= b2—a2,则△ABC是直角三角形,且∠C=90°。
C.如果(c+a)(c-a)=b2,则△ABC是直角三角形。
D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形
2.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。
3.如图,在操场上竖直立着一根长为2米 的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A、B、C三点能否构成直角三角形?为什么?
4.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
四.反思提升:
(1)你有哪些收获?
(2)你还有那些感到疑惑的地方?
第18章勾股定理复习学案
主备人:李善国
学习目标:
1、明确勾股定理及其逆定理的内容
2、能利用勾股定理解决实际问题
学习过程:
一.知识回顾:通过本章的学习你都学到了
二.学以致用:
知识点一、已知两边求第三边
1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为_____________.
2.已知直角三角形的两边长为3、2,则另一条边长是________________.
3.在数轴上作出表示的点.
4.已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高.求 ①AD的长;②ΔABC的面积.
知识点二、利用列方程求线段的长
5.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
6.如图,某学校(A点)与公路(直线L)的距离为300米,
又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
知识点三、判别一个三角形是否是直角三角形
7、分别以下列四组数为一个三角形的边长:(1)3、4、5(2)5、12、13(3)8、15、17(4)4、5、6,其中能够成直角三角形的有-----------
8、若三角形的三别是a2+b2,2ab,a2-b2(a>b>0),则这个三角形是---------------.
9、如图,在我国沿海有一艘不明国际的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西400.那么甲巡逻艇的航向是怎样的?
三、展示应用
10、直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
11、如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外
壁爬行,要从A点爬到B点,则最少要爬行 cm
12、.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,
高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
13、如图:带阴影部分的半圆的面积是-----------(取3)
14、若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,则这个三角形是______________________.
四、能力提升
15、已知:如图,△ABC中,AB>AC,AD是BC边上的高.
求证:AB2-AC2=BC(BD-DC).
16、如图,四边形ABCD中,F为DC的中点,E为BC上一点,
且.你能说明∠AFE是直角吗?
17. (1)你有哪些收获?
(2)你还有那些感到疑惑的地方?
A
D
E
B
C
6
8
主备 人:李善国
学习目标
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
3.了解我国古代在勾股定理研究方面所取得的成就,激发爱国热情。
重点、难点
1.重点:勾股定理的内容及证明。
2.难点:勾股定理的证明。
学习过程:
1. 自主探究
(1) 画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出斜边AB的长。
(2) 再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长。
你是否发现32+42与52的关系,52+122和132的关系,即 。
对于任意的直角三角形也有这个性质吗?人们把这个性质叫做 。
已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证:a2+b2=c2。
小组成员相互合作,找出不同的证法。
结论:
二.合作交流 1。小组内交流 2。组间交流 3。师生共同归纳
三.展示应用
1.在Rt△ABC,∠C=90°
⑴已知a=b=5,求c。
⑵已知a=1,c=2, 求b。
⑶已知c=17,b=8, 求a。
(4)已知b=15,∠A=30°,求a,c。
2.已知直角三角形的两边长分别为5和12,求第三边。
3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
4.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,
AB⊥AC,∠B=60°,CD=1cm,求BC的长。
四.反思提升:
(1) 你有哪些收获?
(2) 你还有那些感到疑惑的地方?
18.1 勾股定理(二)
主备人:李善国
学习目标
1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
学习重点、难点
1.重点:勾股定理的应用。
2.难点:实际问题向数学问题的转化。
学习过程:
1. 自主探究:
勾股定理在实际的生产生活当中有着广泛的应用。勾股定理的发现和使用解决了许多生活中的问题,今天我们就来运用勾股定理解决一些问题,你可以吗?试一试。
1.教材P74页探究1
二.合作交流 1。组内交流 2。组间交流 3。师生共同归纳
三.展示应用
1. 教材P75页探究2
2.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
3.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是 米,水平距离是 米。
4.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是多少?
5.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为 。
四.反思提升:
(1)你有哪些收获?
(2)你还有那些感到疑惑的地方?
18.2 勾股定理的逆定理(一)
主备人:李善国
学习目标
1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.探究勾股定理的逆定理的证明方法。
3.理解原命题、逆命题、逆定理的概念及关系。
学习重点、难点
1.重点:掌握勾股定理的逆定理及证明。
2.难点:勾股定理的逆定理的证明。
学习过程:
1. 自主探究
(一)复习
1. ⑴怎样判定一个三角形是等腰三角形?
⑵怎样判定一个三角形是直角三角形?和等腰三角形的判定进行对比,从勾股定理的逆命题进行猜想。
2.说出下列命题的逆命题,这些命题的逆命题成立吗?
⑴同旁内角互补,两条直线平行。
⑵如果两个实数的平方相等,那么两个实数平方相等。
⑶线段垂直平分线上的点到线段两端点的距离相等。
⑷直角三角形中30°角所对的直角边等于斜边的一半。
(二)自学
1.例(P82探究)
证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
2. 合作交流 1。组内交流 2。组间交流 3。师生共同归纳
三。展示应用
1.下列四条线段不能组成直角三角形的是( )
A.a=8,b=15,c=17
B.a=9,b=12,c=15
C.a=,b=,c=
D.a:b:c=2:3:4
2.叙述下列命题的逆命题,并判断逆命题是否正确。
⑴如果a3>0,那么a2>0;
⑵如果三角形有一个角小于90°,那么这个三角形是锐角三角形;
⑶如果两个三角形全等,那么它们的对应角相等;
⑷关于某条直线对称的两条线段一定相等。
3.填空题。
⑴任何一个命题都有 ,但任何一个定理未必都有 。
⑵“两直线平行,内错角相等。”的逆定理是 。
⑶在△ABC中,若a2=b2-c2,则△ABC是 三角形, 是直角;若a2<b2-c2,则∠B是 。
⑷若在△ABC中,a=m2-n2,b=2mn,c= m2+n2,则△ABC是 三角形。
4.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?
⑴a=9,b=41,c=40;
(2)a=5k,b=12k,c=13k(k>0)。
四.反思提升:
(3) 你有哪些收获?
(4) 你还有那些感到疑惑的地方?
18.2 勾股定理的逆定理(二)
主备人:李善国
学习目标
1.灵活应用勾股定理及逆定理解决实际问题。
2.进一步加深性质定理与判定定理之间关系的认识。
学习重点、难点
1.重点:灵活应用勾股定理及逆定理解决实际问题。
2.难点:灵活应用勾股定理及逆定理解决实际问题。
学习过程:
1. 自主探究
1.(P83例2)
2.一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
2. 合作交流
1. 组内交流
2。组间交流 3。师生共同归纳
3. 展示应用
1.△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形。
B.如果c2= b2—a2,则△ABC是直角三角形,且∠C=90°。
C.如果(c+a)(c-a)=b2,则△ABC是直角三角形。
D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形
2.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。
3.如图,在操场上竖直立着一根长为2米 的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A、B、C三点能否构成直角三角形?为什么?
4.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
四.反思提升:
(1)你有哪些收获?
(2)你还有那些感到疑惑的地方?
第18章勾股定理复习学案
主备人:李善国
学习目标:
1、明确勾股定理及其逆定理的内容
2、能利用勾股定理解决实际问题
学习过程:
一.知识回顾:通过本章的学习你都学到了
二.学以致用:
知识点一、已知两边求第三边
1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为_____________.
2.已知直角三角形的两边长为3、2,则另一条边长是________________.
3.在数轴上作出表示的点.
4.已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高.求 ①AD的长;②ΔABC的面积.
知识点二、利用列方程求线段的长
5.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
6.如图,某学校(A点)与公路(直线L)的距离为300米,
又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
知识点三、判别一个三角形是否是直角三角形
7、分别以下列四组数为一个三角形的边长:(1)3、4、5(2)5、12、13(3)8、15、17(4)4、5、6,其中能够成直角三角形的有-----------
8、若三角形的三别是a2+b2,2ab,a2-b2(a>b>0),则这个三角形是---------------.
9、如图,在我国沿海有一艘不明国际的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西400.那么甲巡逻艇的航向是怎样的?
三、展示应用
10、直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
11、如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外
壁爬行,要从A点爬到B点,则最少要爬行 cm
12、.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,
高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
13、如图:带阴影部分的半圆的面积是-----------(取3)
14、若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,则这个三角形是______________________.
四、能力提升
15、已知:如图,△ABC中,AB>AC,AD是BC边上的高.
求证:AB2-AC2=BC(BD-DC).
16、如图,四边形ABCD中,F为DC的中点,E为BC上一点,
且.你能说明∠AFE是直角吗?
17. (1)你有哪些收获?
(2)你还有那些感到疑惑的地方?
A
D
E
B
C
6
8
