广西玉林市人教版九年级数学上册 第22章 二次函数知识点讲授(包含玉林市2010~2016年中考题)
文档属性
| 名称 | 广西玉林市人教版九年级数学上册 第22章 二次函数知识点讲授(包含玉林市2010~2016年中考题) |
|
|
| 格式 | zip | ||
| 文件大小 | 136.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-09 00:00:00 | ||
图片预览

文档简介
第22章 二次函数知识点讲授
一、重做中考题:2010~2016年近七年玉林中考的考题
(一)选择与填空的考查
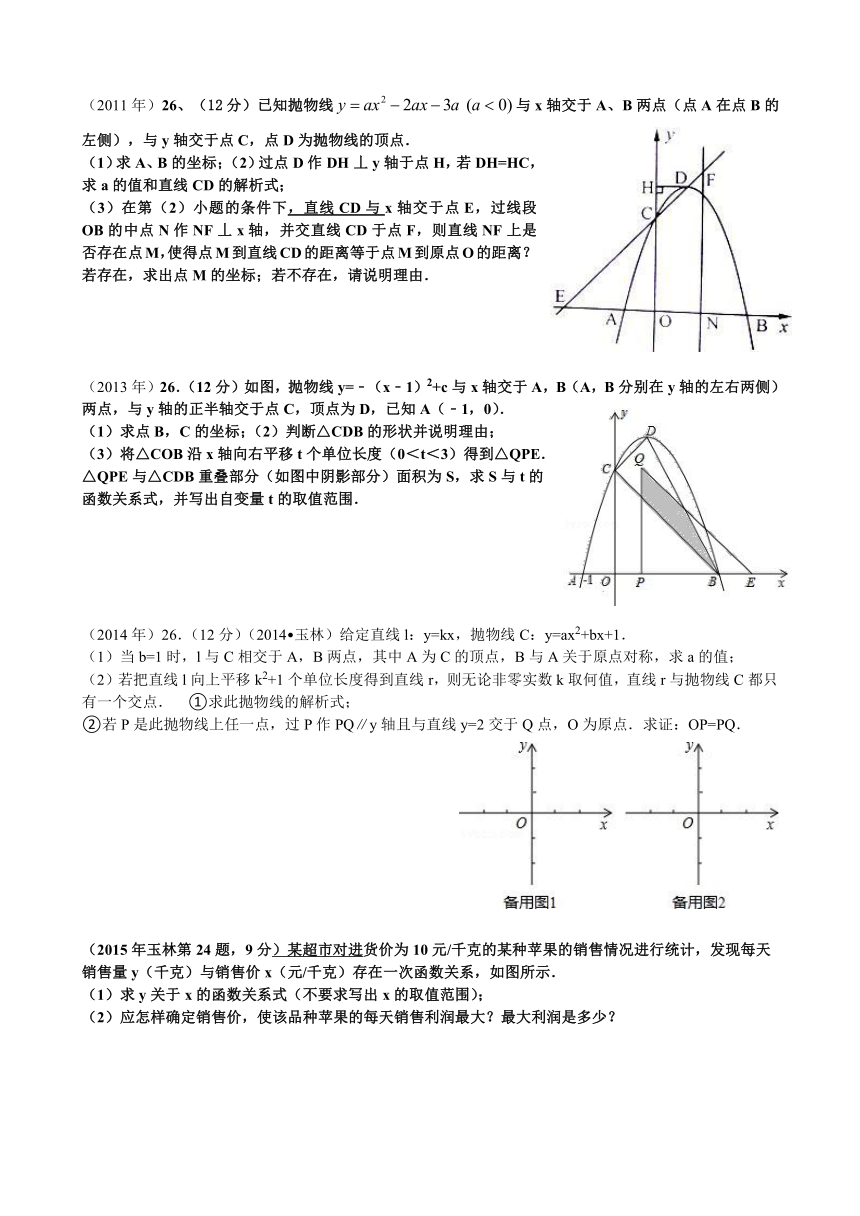
1.(2010年第6题)已知二次函数y=ax2的图象开口向上,则直线y=ax-1经过的象限是( )
A、第一、二、三象限
B、第二、三、四象限
C、第一、二、四象限
D、第一、三、四象限
2.(2011年第9题)已知拋物线y=﹣x2+2,当1≤x≤5时,y的最大值是( )A、2 B、 C、
D、
3.(2012年第11题)二次函数(≠0)的图像如图所示,其对称轴为=1,有如下结论:①
<1
②2+=0
③<4
④若方程的两个根为,,则+=2.则结论正确的是( )A.
①②
B.
①③
C.
②④
D.
③④
4.(2012年第18题)二次函数的图像与轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有
个(提示:必要时可利用下面的备用图画出图像来分析).
5.(2015年第12题)如图,反比例函数的图象经过二次函数图象的顶点(,
m)
(m>0),则有( )A.
B.
C.
D.
( http: / / www.21cnjy.com )
7.(2016年第8题)8.抛物线y=,y=x2,y=﹣x2的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对称轴;④都关于x轴对称.
其中正确的个数有( )A.1个
B.2个
C.3个
D.4个
(二)大题的考查
(2010年)26.(12分)已知:抛物线与轴交于A、B两点,与轴交于C点,且。点B在轴的正半轴上,OC=3OA(O为坐标原点)。(1)求抛物线的解析式;
(2)若点E是抛物线上的一个动点且在轴下方和抛物线对称轴l的左侧,过E作EF∥轴交抛物线与另一点F,作ED⊥轴于点D,FG⊥轴于点G。求四边形DEFG周长的最大值;
(3)设抛物线顶点为P,当四边形DEFG周长取得最大值时,以EF为边的平行四边形面积是△AEP面积的2倍,另两顶点中有一顶点Q在抛物线上,求Q点的坐标。
( http: / / www.21cnjy.com )
(2011年)26、(12分)已知抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B的坐标;(2)过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;
(3)在第(2)小题的条件下,直线CD与
( http: / / www.21cnjy.com )x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
(2013年)26.(12分)如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.
△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的
函数关系式,并写出自变量t的取值范围.
(2014年)26.(12分)(2014 玉林)给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点. ①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.
( http: / / www.21cnjy.com )
(2015年玉林第24题,9分)某超市对进
( http: / / www.21cnjy.com )货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
(2016年)26.如图,抛物线L:y=a
( http: / / www.21cnjy.com )x2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1. (1)求抛物线L的解析式;
(2)将抛物线L向下平移h
( http: / / www.21cnjy.com )个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围; (3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
二、本章知识要点概括
1.二次函数定义:形如的函数称为二次函数。
2.二次函数的图象:二次函数的图象是一条曲线,称为抛物线。
3.二次函数的对称轴为;顶点坐标为
。
开口方向:当a>0时,开口方向向上;当
( http: / / www.21cnjy.com )a<0时,开口方向向下;开口大小由|a|决定,
|a|越小开口越大;
|a|越大开口越小;开口大小相同,则|a|相等;
对称轴位置:当a、b同号时,对称轴
( http: / / www.21cnjy.com )在y轴左侧;当a、b异号时,对称轴在y轴右侧;当b=0时,对称轴与y轴重合;用四个字总结对称轴与y轴的位置关系为“左同右异”;
二次函数的最值:当a>0时,二次函数在处取得最小值;当a<0时,二次函数在处取得最大值。
4.二次函数解析式的三种表示形式:①一般式:
②顶点式:
③交点式:其中是方程的两个实根。
5.⑴当时,y随x的增大而减小;时,y随x的增大而增大。
⑵当时,
y随x的增大而增大;时,y随x的增大而减小。
6.当时,抛物线与x轴有2个交点,关于对称,交点之间的距离为。
当时,抛物线与x轴有1个交点,即为抛物线的顶点。
当时,抛物线与x轴有0个交点。
7.抛物线平移的规律可总结为八个字是“左加右减,上加下减”。
8.抛物线y=ax2+bx+c(a
( http: / / www.21cnjy.com )≠0)关于x轴对称的抛物线解析式为y=-ax2-bx-c;关于y轴对称的抛物线解析式为y=ax2-bx+c;关于原点对称的抛物线解析式为y=-ax2+bx-c
三、基础知识梳理
1.
二次函数的图像和性质
>0
<0
图
象
开
口
对
称
轴
顶点坐标
最
值
当x=
时,y有最
值
当x=
时,y有最
值
增减性
在对称轴左侧
y随x的增大而
y
随x的增大而
在对称轴右侧
y随x的增大而
y随x的增大而
2.
二次函数用配方法可化成的形式,其中=
,
=
.
3.二次函数的对称轴是,其中是方程的两个实根
4.
二次函数的图像和图像的关系.
5.
二次函数中的符号的确定.(1)决定开口方向及开口大小,这与中的完全一样.
(2)和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线,故:①时,对称轴为轴;②(即、同号)时,对称轴在轴左侧;③(即、异号)时,对称轴在轴右侧.
(3)的大小决定抛物线与轴交点的位置.
当时,,∴抛物线与轴有且只有一个交点(0,):
①,抛物线经过原点;
②,与轴交于正半轴;③,与轴交于负半轴.
y
x
O
一、重做中考题:2010~2016年近七年玉林中考的考题
(一)选择与填空的考查
1.(2010年第6题)已知二次函数y=ax2的图象开口向上,则直线y=ax-1经过的象限是( )
A、第一、二、三象限
B、第二、三、四象限
C、第一、二、四象限
D、第一、三、四象限
2.(2011年第9题)已知拋物线y=﹣x2+2,当1≤x≤5时,y的最大值是( )A、2 B、 C、
D、
3.(2012年第11题)二次函数(≠0)的图像如图所示,其对称轴为=1,有如下结论:①
<1
②2+=0
③<4
④若方程的两个根为,,则+=2.则结论正确的是( )A.
①②
B.
①③
C.
②④
D.
③④
4.(2012年第18题)二次函数的图像与轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有
个(提示:必要时可利用下面的备用图画出图像来分析).
5.(2015年第12题)如图,反比例函数的图象经过二次函数图象的顶点(,
m)
(m>0),则有( )A.
B.
C.
D.
( http: / / www.21cnjy.com )
7.(2016年第8题)8.抛物线y=,y=x2,y=﹣x2的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以y轴为对称轴;④都关于x轴对称.
其中正确的个数有( )A.1个
B.2个
C.3个
D.4个
(二)大题的考查
(2010年)26.(12分)已知:抛物线与轴交于A、B两点,与轴交于C点,且。点B在轴的正半轴上,OC=3OA(O为坐标原点)。(1)求抛物线的解析式;
(2)若点E是抛物线上的一个动点且在轴下方和抛物线对称轴l的左侧,过E作EF∥轴交抛物线与另一点F,作ED⊥轴于点D,FG⊥轴于点G。求四边形DEFG周长的最大值;
(3)设抛物线顶点为P,当四边形DEFG周长取得最大值时,以EF为边的平行四边形面积是△AEP面积的2倍,另两顶点中有一顶点Q在抛物线上,求Q点的坐标。
( http: / / www.21cnjy.com )
(2011年)26、(12分)已知抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B的坐标;(2)过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;
(3)在第(2)小题的条件下,直线CD与
( http: / / www.21cnjy.com )x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
(2013年)26.(12分)如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.
△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的
函数关系式,并写出自变量t的取值范围.
(2014年)26.(12分)(2014 玉林)给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点. ①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.
( http: / / www.21cnjy.com )
(2015年玉林第24题,9分)某超市对进
( http: / / www.21cnjy.com )货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
(2016年)26.如图,抛物线L:y=a
( http: / / www.21cnjy.com )x2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1. (1)求抛物线L的解析式;
(2)将抛物线L向下平移h
( http: / / www.21cnjy.com )个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围; (3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
二、本章知识要点概括
1.二次函数定义:形如的函数称为二次函数。
2.二次函数的图象:二次函数的图象是一条曲线,称为抛物线。
3.二次函数的对称轴为;顶点坐标为
。
开口方向:当a>0时,开口方向向上;当
( http: / / www.21cnjy.com )a<0时,开口方向向下;开口大小由|a|决定,
|a|越小开口越大;
|a|越大开口越小;开口大小相同,则|a|相等;
对称轴位置:当a、b同号时,对称轴
( http: / / www.21cnjy.com )在y轴左侧;当a、b异号时,对称轴在y轴右侧;当b=0时,对称轴与y轴重合;用四个字总结对称轴与y轴的位置关系为“左同右异”;
二次函数的最值:当a>0时,二次函数在处取得最小值;当a<0时,二次函数在处取得最大值。
4.二次函数解析式的三种表示形式:①一般式:
②顶点式:
③交点式:其中是方程的两个实根。
5.⑴当时,y随x的增大而减小;时,y随x的增大而增大。
⑵当时,
y随x的增大而增大;时,y随x的增大而减小。
6.当时,抛物线与x轴有2个交点,关于对称,交点之间的距离为。
当时,抛物线与x轴有1个交点,即为抛物线的顶点。
当时,抛物线与x轴有0个交点。
7.抛物线平移的规律可总结为八个字是“左加右减,上加下减”。
8.抛物线y=ax2+bx+c(a
( http: / / www.21cnjy.com )≠0)关于x轴对称的抛物线解析式为y=-ax2-bx-c;关于y轴对称的抛物线解析式为y=ax2-bx+c;关于原点对称的抛物线解析式为y=-ax2+bx-c
三、基础知识梳理
1.
二次函数的图像和性质
>0
<0
图
象
开
口
对
称
轴
顶点坐标
最
值
当x=
时,y有最
值
当x=
时,y有最
值
增减性
在对称轴左侧
y随x的增大而
y
随x的增大而
在对称轴右侧
y随x的增大而
y随x的增大而
2.
二次函数用配方法可化成的形式,其中=
,
=
.
3.二次函数的对称轴是,其中是方程的两个实根
4.
二次函数的图像和图像的关系.
5.
二次函数中的符号的确定.(1)决定开口方向及开口大小,这与中的完全一样.
(2)和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线,故:①时,对称轴为轴;②(即、同号)时,对称轴在轴左侧;③(即、异号)时,对称轴在轴右侧.
(3)的大小决定抛物线与轴交点的位置.
当时,,∴抛物线与轴有且只有一个交点(0,):
①,抛物线经过原点;
②,与轴交于正半轴;③,与轴交于负半轴.
y
x
O
同课章节目录
