相似三角形的概念

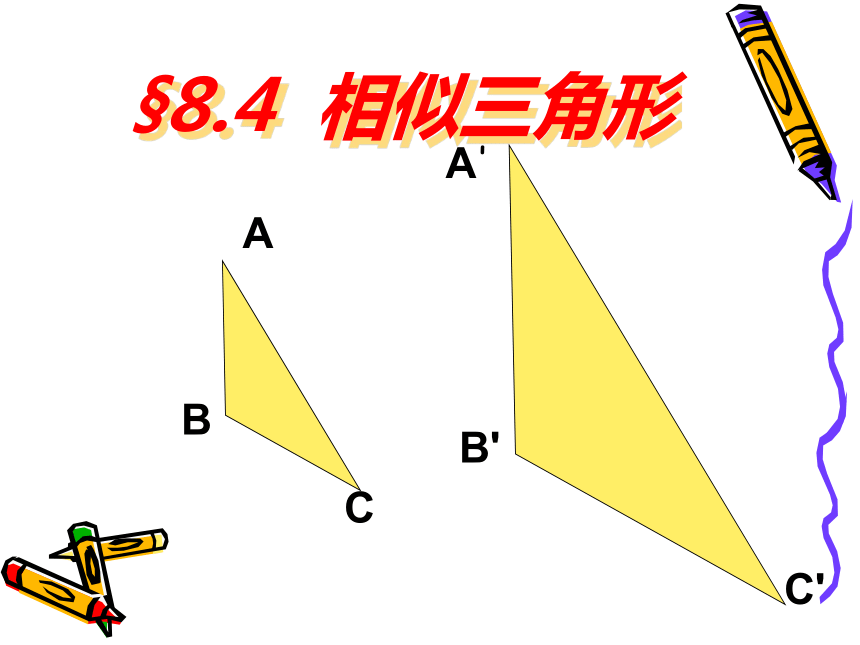
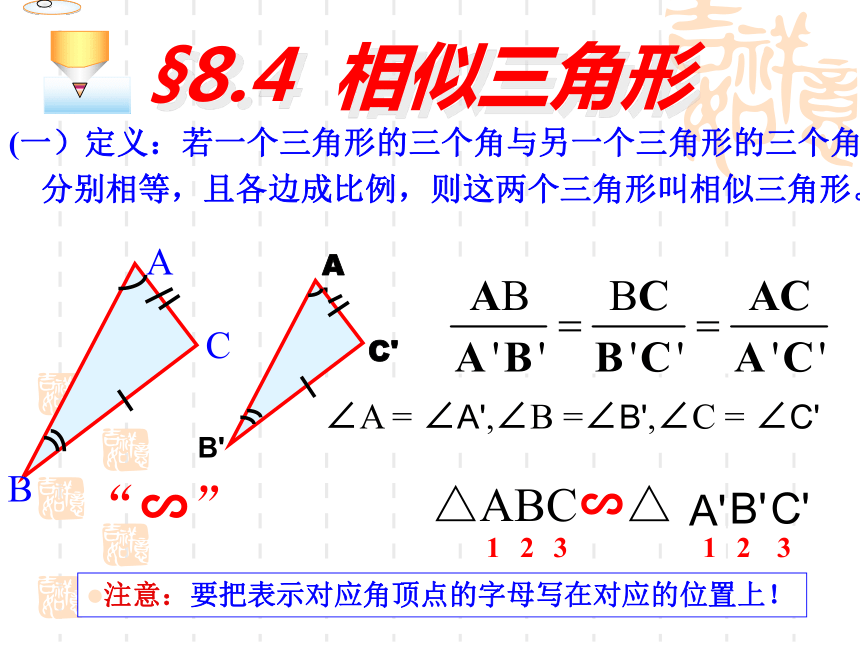
课件17张PPT。8.4 相似三角形青岛版 数学 八年级 下认真观察下图，哪些图形是相似图形？ 1234ABCD§8.4 相似三角形ABCB'C'A'(一）定义：若一个三角形的三个角与另一个三角形的三个角分别相等，且各边成比例，则这两个三角形叫相似三角形。§8.4 相似三角形∠A = ∠A',∠B =∠B',∠C = ∠C'△ABC∽△ “∽”注意：要把表示对应角顶点的字母写在对应的位置上！123123
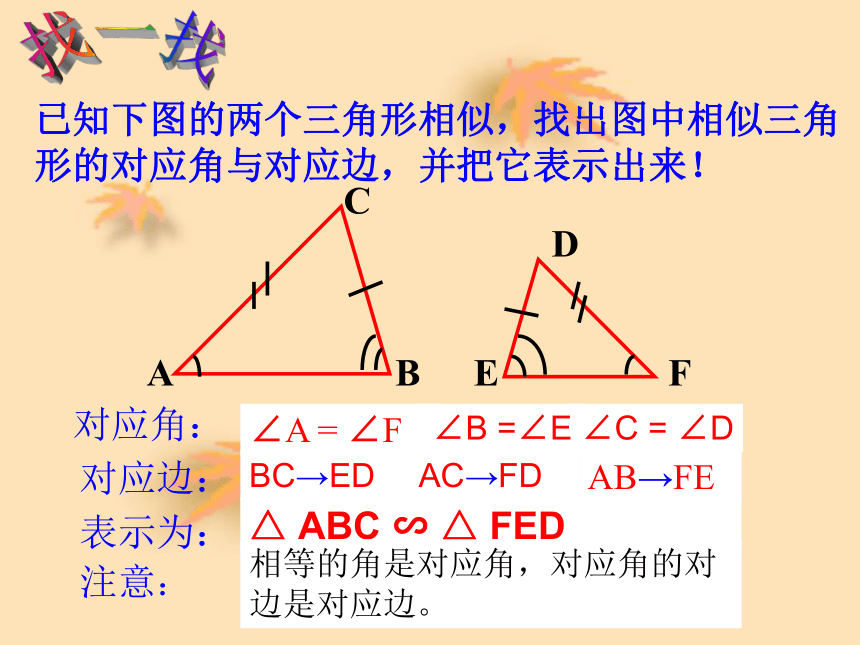
A'B'C'找一找已知下图的两个三角形相似，找出图中相似三角形的对应角与对应边，并把它表示出来！对应角：对应边：表示为：△ ABC ∽ △ FED∠A = ∠FAB→FE注意：相等的角是对应角，对应角的对边是对应边。∠B =∠E∠C = ∠DBC→EDAC→FDDE（二）相似三角形的性质：
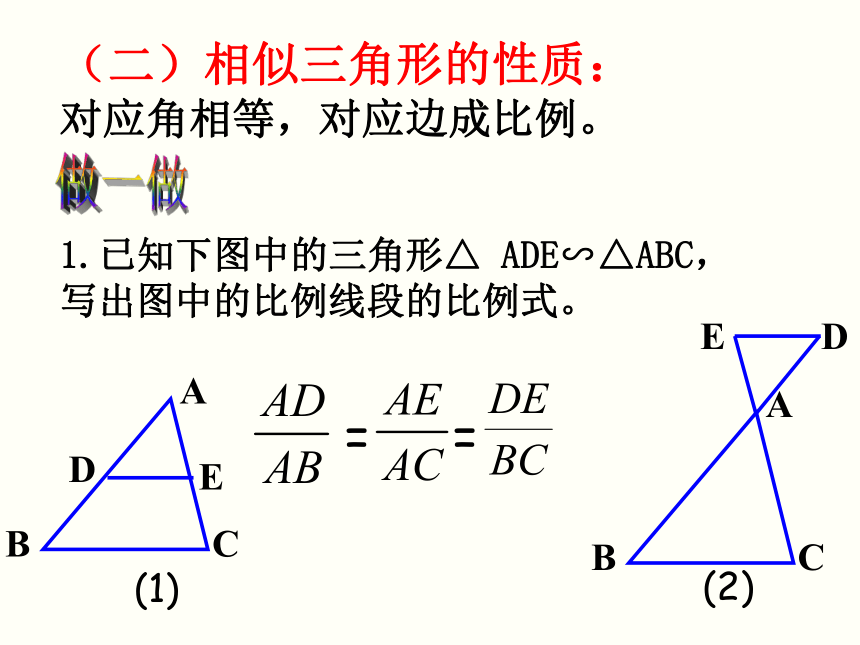
对应角相等，对应边成比例。做一做1.已知下图中的三角形△ ADE∽△ABC，写出图中的比例线段的比例式。==(1)(2)2.如图， △BCA ∽ △BAD,写出图中所
所有相等的角和成比例线段的比例式。ABDC∠ABC=∠DBA,∠BAC=∠BDA，∠BCA=∠BAD。==思考：△ DEF 与 △ ABC的相似比是多少呢？也是 吗？那么：则△ ABC 与 △ DEF的相似比就是 。（三）相似比：如 果 注意：相似比具有顺序性！当相似比为1是，这两个三角形有什么关系？思考： 如图：已知△ADE∽△ABC。 （1）如果∠A=70°∠B=65°，求
∠ADE和∠AED的度数；
（2）如果AD=6，DB=3，BC=12,求DE的长。解：(1)∵△ADE∽△ABC
∴∠ADE=在△ADE中，
∠AED=180°-∠ADE-∠A
=180°-65°-70°
=45°∠B=65°应用 提高（四）解：（2）∵△ADE∽△ABC, 即 =∴ =变式训练如图：△ADE∽△ABC
（1） DE//BC吗？
（2）若AD=2，DE=4，BC=9，求BD的长。∴DE=8。随堂练习1.如果△ABC∽△A'B'C'，∠ACB=50°，则
∠A'C'B'=????????????.
2.已知△ABC∽△DEF，若∠A=30°，
∠B=90°，则∠F=??????????；
若AB=2，BC=3,DE=1,则EF=???????????。
3.如图，已知△ABC∽△EDC，下列
结论错误的是（ ）
A.AB:DE=AC:EC
B.AC:BC=EC:DC
C.AE:AC=BD:BC
D.AB//DEABCDE50°60°C1、两个全等三角形一定相似吗？为什么？相似.因为对应角相等,对应边成比例２、两个直角三角形一定相似吗？为什么？两个直角三角形不一定相似。因为对应角不一定相等，对应边也不一定成比例. 3 、两个等腰直角三角形呢？4、两个等腰三角形一定相似吗？为什么？5 、两个等边三角形呢？两个等腰三角形不一定相似;两个等腰直角三角形相似.因为对应角相等,对应边成比例.两个等边三角形相似.1、下面的两个图形是相似三角形，
试确定x , m , n 的值。 x=12
m=80°
n=55°2、如果一个三角形的三边长分别是6、8和10，与其相似的三角形的最短边长是15，那么较大三角形的周长是多少？（较大三角形周长是60）（五）巩固与提高三个角对应相等,三条边对应成比例的两个三角形,
叫做相似三角形。
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意：要把表示对应角顶点的字母写在对应的位置上！
性质：相似三角形的各对应角相等,各对应边对应成比例。
如果△ ABC∽ △DEF,那么∠A = ∠D,∠B = ∠E,∠C = ∠F.相似比为1的两个相似三角形是什么样的关系？全等三角形你有什么收获吗全等一定相似，但相似不一定全等知 识 的 升 华习题 8.4祝 你 成 功！作业书山有路勤为径
学海无涯苦作舟再 见老 师 寄 语