江苏省常州市武进区2015-2016学年高二(上)期末数学试卷(文科)(解析版)
文档属性
| 名称 | 江苏省常州市武进区2015-2016学年高二(上)期末数学试卷(文科)(解析版) | 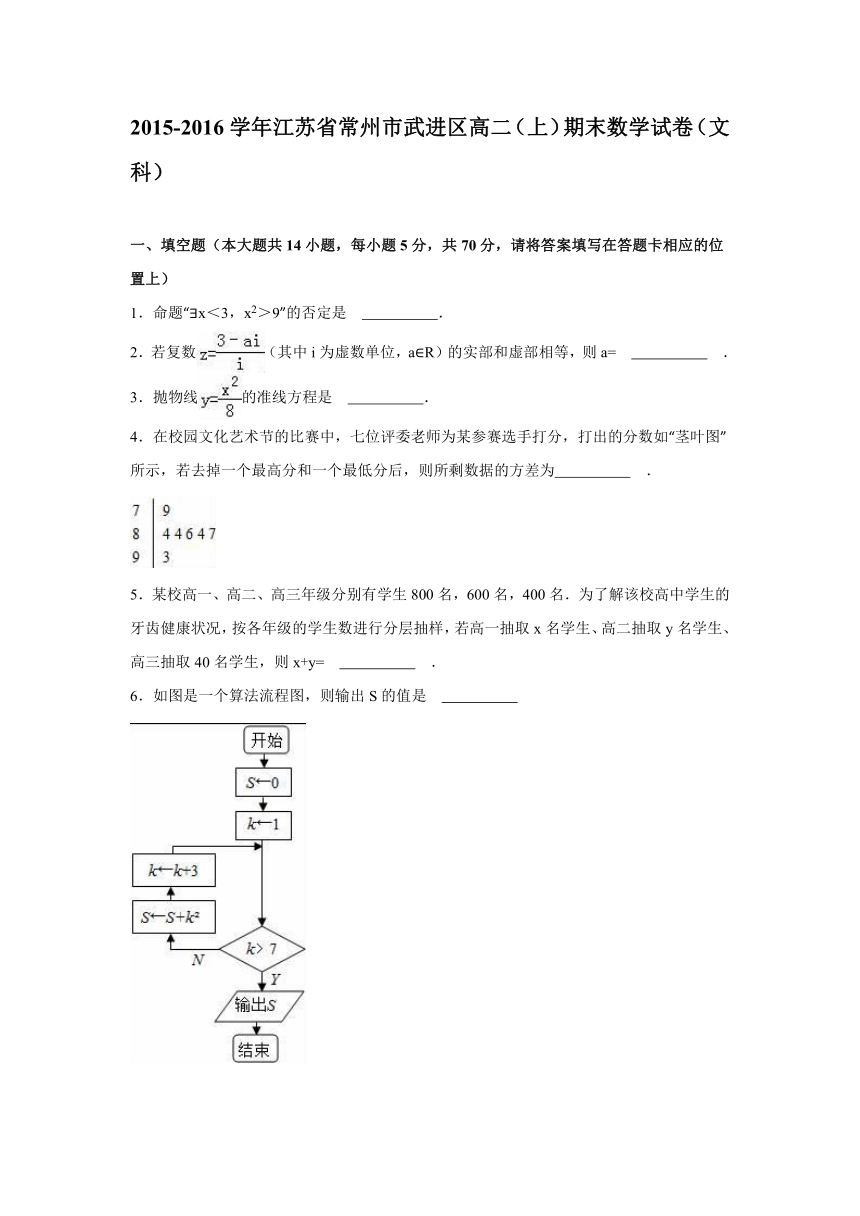 | |
| 格式 | zip | ||
| 文件大小 | 270.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-10 22:20:16 | ||
图片预览




文档简介
2015-2016学年江苏省常州市武进区高二(上)期末数学试卷(文科)
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)
1.命题“ x<3,x2>9”的否定是 .
2.若复数(其中i为虚数单位,a∈R)的实部和虚部相等,则a= .
3.抛物线的准线方程是 .
4.在校园文化艺术节的比赛中,七位评委老师为某参赛选手打分,打出的分数如“茎叶图”所示,若去掉一个最高分和一个最低分后,则所剩数据的方差为 .
5.某校高一、高二、高三年级分别有学生800名,600名,400名.为了解该校高中学生的牙齿健康状况,按各年级的学生数进行分层抽样,若高一抽取x名学生、高二抽取y名学生、高三抽取40名学生,则x+y= .
6.如图是一个算法流程图,则输出S的值是
7.已知m,n∈N
且n>m,在公比为q的等比数列{an}中,有an=amqn﹣m成立,类似地,在公差为d的等差数列{bn}中,有 成立.
8.设a∈R,则“a=1”是“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”的 条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
9.一只蚂蚁在高为3,两底分别为3和7的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为 .
10.已知曲线y=lnx+2在点P处的切线经过点A(0,1),则此切线的方程为 .
11.若椭圆和双曲线有相同的焦点F1,F2,点P是两条曲线的一个交点,则PF1PF2的值是 .
12.已知g(x)=x3﹣x2﹣x﹣1,若对 x1,x2∈[0,2],都有m≤g(x1)﹣g(x2)成立,则m的最大值为
13.已知函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,则满足f(x)<0的x的取值范围为 .
14.已知椭圆=1(a>b>0)的右焦点为F,其右准线与x轴的交点为A,若在椭圆上存在点P满足PF=AF,则﹣2(lnc﹣lna)的范围是 .
二、解答题:(本大题共6小题,共计90分.请把答案写在答题卡相应的位置上.解答时应写出文字说明,证明过程或演算步骤.)
15.设命题p:复数z=(m+1)+(m﹣4)i在复平面上对应的点在第一或第三象限,命题q:方程表示双曲线,若“p且q”为真命题,则求实数m的取值范围.
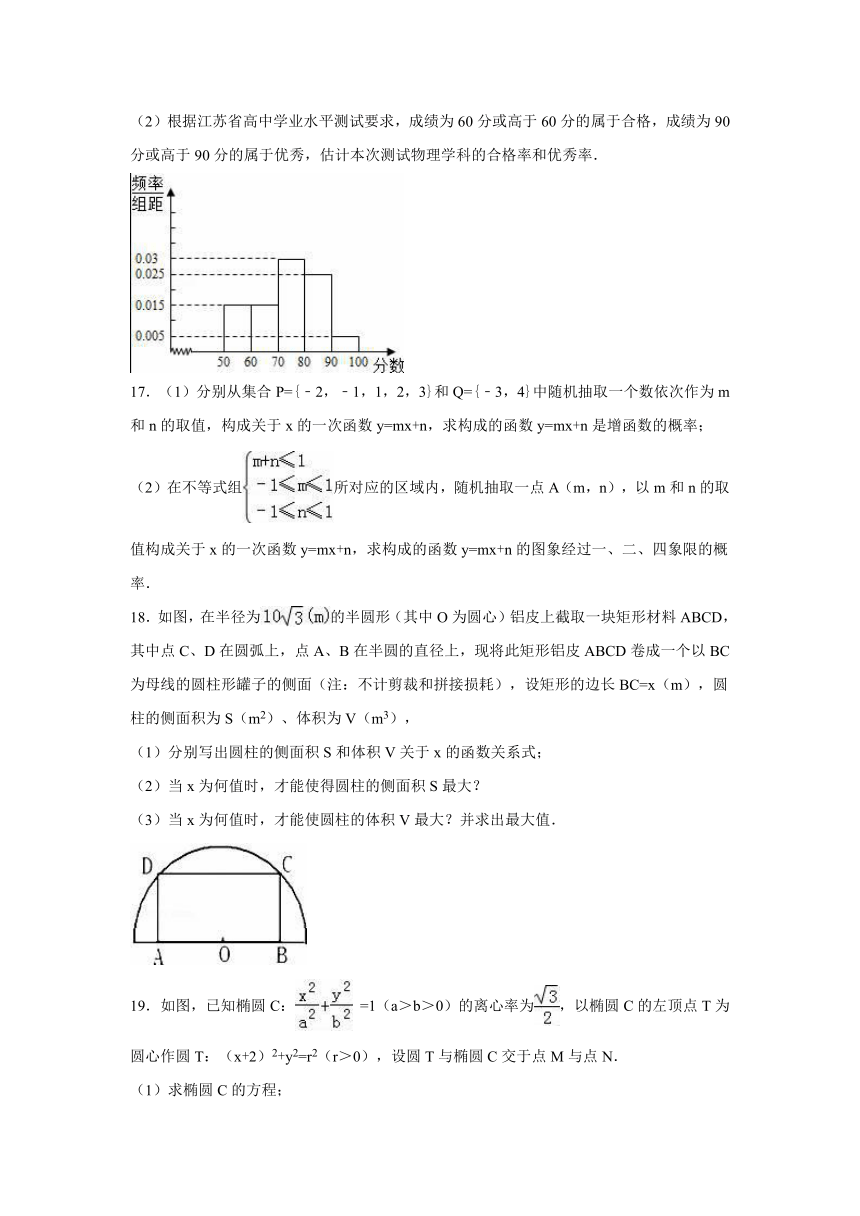
16.为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
(1)根据江苏省高中学业水平测试要求,成绩低于60分的属于不合格需要补考,求抽取的60名学生中需要补考的学生人数;
(2)根据江苏省高中学业水平测试要求,成绩为60分或高于60分的属于合格,成绩为90分或高于90分的属于优秀,估计本次测试物理学科的合格率和优秀率.
17.(1)分别从集合P={﹣2,﹣1,1,2,3}和Q={﹣3,4}中随机抽取一个数依次作为m和n的取值,构成关于x的一次函数y=mx+n,求构成的函数y=mx+n是增函数的概率;
(2)在不等式组所对应的区域内,随机抽取一点A(m,n),以m和n的取值构成关于x的一次函数y=mx+n,求构成的函数y=mx+n的图象经过一、二、四象限的概率.
18.如图,在半径为的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
(1)分别写出圆柱的侧面积S和体积V关于x的函数关系式;
(2)当x为何值时,才能使得圆柱的侧面积S最大?
(3)当x为何值时,才能使圆柱的体积V最大?并求出最大值.
19.如图,已知椭圆C:
=1(a>b>0)的离心率为,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
(1)求椭圆C的方程;
(2)求的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
20.已知函数f(x)=lnx,,设F(x)=f(x)+g(x),
(1)当a=2时,求函数F(x)的单调区间;
(2)若函数y=F(x)(x∈(0,1])图象上任意一点P(x0,y0)为切点的切线的斜率记为k,且k≤1恒成立,求实数a的最大值;
(3)是否存在实数m,使得函数的图象与函数的图象恰有三个不同交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
2015-2016学年江苏省常州市武进区高二(上)期末数学试卷(文科)
参考答案与试题解析
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)
1.命题“ x<3,x2>9”的否定是 x<3,x2≤9 .
【分析】直接利用特称命题的否定是全称命题写出结果即可.
【解答】解:因为特称命题的否定是全称命题,所以命题“ x<3,x2>9”的否定是: x<3,x2≤9,
故答案为: x<3,x2≤9.
【点评】本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.
2.若复数(其中i为虚数单位,a∈R)的实部和虚部相等,则a= 3 .
【分析】直接由复数代数形式的乘除运算化简复数z,又由复数z的实部和虚部相等,则a可求.
【解答】解:∵
=,
又复数(其中i为虚数单位,a∈R)的实部和虚部相等,
∴﹣a=﹣3即a=3.
故答案为:3.
【点评】本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.
3.抛物线的准线方程是 y=﹣2 .
【分析】将抛物线的方程化为标准方程,再由x2=2py的准线方程y=﹣,即可得到所求方程.
【解答】解:抛物线,即为
x2=8y,即有2p=8,
可得﹣=﹣2.
则准线方程为y=﹣2.
故答案为:y=﹣2.
【点评】本题考查抛物线的准线方程的求法,考查运算能力,属于基础题.
4.在校园文化艺术节的比赛中,七位评委老师为某参赛选手打分,打出的分数如“茎叶图”所示,若去掉一个最高分和一个最低分后,则所剩数据的方差为 .
【分析】根据题意,计算去掉一个最高分和一个最低分后的平均数与方差即可.
【解答】解:根据茎叶图中的数据,计算去掉一个最高分93,一个最低分79后,
所剩数据的平均数是=×(84+84+86+84+87)=85,
方差是s2=×[(84﹣85)2×3+(86﹣85)2+(87﹣85)2]=.
故答案为:.
【点评】本题考查了利用茎叶图中的数据计算平均数与方差的应用问题,是基础题目.
5.某校高一、高二、高三年级分别有学生800名,600名,400名.为了解该校高中学生的牙齿健康状况,按各年级的学生数进行分层抽样,若高一抽取x名学生、高二抽取y名学生、高三抽取40名学生,则x+y= 140 .
【分析】根据分层抽样的定义,建立比例关系,即可得到结论.
【解答】解:∵高一、高二、高三分别有学生800名,600名,400名,
∴若高三抽取40名学生,设共需抽取的学生数为m,
则=,解得m=180,
则高一、高二共需抽取的学生数为x+y=180﹣40=140,
故答案为:140.
【点评】本题主要考查分层抽样的应用,比较基础.
6.如图是一个算法流程图,则输出S的值是 66 .
【分析】模拟程序框图的运行过程,即可得出输出的S值.
【解答】解:第1次循环得S=0+1=1,k=4,此时不满足判断框的条件,
第2次循环得S=1+42=17,k=7,此时不满足判断框的条件,
第3次循环得S=17+72,k=10,此时满足判断框的条件,
输出S=66,结束程序.
故答案为:66.
【点评】本题考查了程序框图的应用问题,解题时应模拟程序语言的运行过程,是基础题目.
7.已知m,n∈N
且n>m,在公比为q的等比数列{an}中,有an=amqn﹣m成立,类似地,在公差为d的等差数列{bn}中,有 bn=bm+(n﹣m)d 成立.
【分析】等差数列{an}中,给出第m项bm和公差,求出首项,再把首项代入等差数列的通项公式中,即可得到结论.
【解答】解:在公差为d的等差数列{bn}中,设其首项为b1,则bm=b1+(m﹣1)d,
∴b1=bm+(1﹣m)d,
则bn=b1+(n﹣1)d=bm+(n﹣m)d,
故答案为:bn=bm+(n﹣m)d.
【点评】本题考查了类比推理,类比推理就是根据两个不同的对象在某些方面的相似之处,从而推出这两个对象在其他方面的也具有的相似之处,是基础题.
8.设a∈R,则“a=1”是“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”的 充分不必要 条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
【分析】利用a=1判断两条直线是否平行;通过两条直线平行是否推出a=1,即可得到答案.
【解答】解:因为“a=1”时,“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0”
化为l1:x+2y﹣1=0与l2:x+2y+4=0,显然两条直线平行;
如果“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”
必有a(a+1)=2,解得a=1或a=﹣2,
所以“a=1”是“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”的充分不必要条件.
故答案为:充分不必要.
【点评】本题考查充要条件的判断,能够正确判断两个命题之间的条件与结论的推出关系是解题的关键.
9.一只蚂蚁在高为3,两底分别为3和7的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为 .
【分析】以四个顶点为圆心,1为半径作圆,当蚂蚁在此区域外的区域随机爬行,离顶点的距离大于1,其面积为15﹣π,再用几何概型公式即得本题的概率
【解答】解:如图由已知,高为3,两底分别为3和7的直角梯形面积为×3×(3+7)=15,
离四个顶点距离都大于1的区域是如图阴影部分,即以四个顶点为圆心,1为半径作圆,当蚂蚁在除此区域外的区域随机爬行,离顶点的距离大于1的部分,其面积为=15﹣π,
∴蚂蚁恰在离四个顶点距离都大于1的地方的概率为P=.
故答案为:.
【点评】本题几何概型的概率.着重考查了图形面积的求法和几何概型的概率求法等知识点,属于基础题.
10.已知曲线y=lnx+2在点P处的切线经过点A(0,1),则此切线的方程为 x﹣y+1=0 .
【分析】设P(m,n),即有n=lnm+2,求出函数的导数,求得切线的斜率,再由两点的斜率公式,解方程可得m=1,再由斜截式方程可得切线的方程.
【解答】解:设P(m,n),即有n=lnm+2,
y=lnx+2的导数为y′=,
即有切线的斜率为k=,
由题意可得=,
解得m=1,n=2,
即有切线的方程为y=x+1.
即为x﹣y+1=0.
故答案为:x﹣y+1=0.
【点评】本题考查导数的运用:求切线的方程,正确求导和运用直线的斜率公式是解题的关键,属于基础题.
11.若椭圆和双曲线有相同的焦点F1,F2,点P是两条曲线的一个交点,则PF1PF2的值是 16 .
【分析】根据点P为椭圆和双曲线的一个交点,结合椭圆和双曲线的第一定义求出|PF1|与|PF2|的表达式,解方程,即可求出|PF1||PF2|的值.
【解答】解:因为椭圆和双曲线有相同的焦点F1,F2,
设P在双曲线的右支上,
利用椭圆以及双曲线的定义可得:|PF1|+|PF2|=2×5=10①
|PF1|﹣|PF2|=2×3=6②
由①②得:|PF1|=8,|PF2|=2.
∴|PF1||PF2|=16.
故答案为:16.
【点评】本题主要考查圆锥曲线的定义、方程和性质,解决本题的关键在于根据椭圆与双曲线有共同的焦点,运用第一定义,考查运算能力,属中档题.
12.已知g(x)=x3﹣x2﹣x﹣1,若对 x1,x2∈[0,2],都有m≤g(x1)﹣g(x2)成立,则m的最大值为 ﹣3 .
【分析】问题转化为m≤g(x)min﹣g(x)max,求出函数g(x)的最大值和最小值,代入求出即可.
【解答】解:g′(x)=3x2﹣2x﹣1=(2x+1)(x﹣1),
令g′(x)>0,解得:x>1,
令g′(x)<0,解得:x<1,
∴g(x)在[0,1)递减,在(1,2]递增;
∴g(x)min=g(1)=﹣2,g(x)max=g(2)=1,
∴m≤g(x)min﹣g(x)max=﹣3,
故答案为:﹣3.
【点评】本题考察了求函数的最值问题,是一道中档题.
13.已知函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,则满足f(x)<0的x的取值范围为 (1,e) .
【分析】求f(x)的导数,利用导数性质能求出满足f(x)<0的x的取值范围.
【解答】解:∵函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,
∴=0,得x=e﹣1,
又f(1)=0,f(e)=0,1<e﹣1<e,
∴由f(x)<0得:1<x<e.
故答案为:(1,e),
【点评】本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意导数性质的合理运用.
14.已知椭圆=1(a>b>0)的右焦点为F,其右准线与x轴的交点为A,若在椭圆上存在点P满足PF=AF,则﹣2(lnc﹣lna)的范围是 (1,
+2ln2] .
【分析】求出椭圆的右焦点和右准线,求得AF的长,再由椭圆的性质,可得a﹣c≤|PF|≤a+c,进而得到a≤2c,a,c的关系,令t=(≤t<1),则f(t)=t2﹣2lnt,运用导数判断单调性,即可得到所求范围.
【解答】解:椭圆=1(a>b>0)的右焦点F(c,0),右准线为x=,
由题意|PF|=|AF|=﹣c,
由椭圆的性质可得a﹣c≤|PF|≤a+c,
即有a﹣c≤﹣c≤a+c,
即有c<a+c且a﹣c≤c,
则有a≤2c,
即为≤<1,
则﹣2(lnc﹣lna)=()2﹣2ln,
令t=(≤t<1),
则f(t)=t2﹣2lnt,
由f′(t)=2t﹣<0在[,1)成立,
则有f(t)在[,1]递减,
故f(t)的范围为(1,
+2ln2].
故答案为:(1,
+2ln2].
【点评】本题考查椭圆的方程和性质,主要考查椭圆的准线方程的运用,椭圆上一点到焦点的距离的最值,同时考查导数的运用:判断单调性,属于中档题.
二、解答题:(本大题共6小题,共计90分.请把答案写在答题卡相应的位置上.解答时应写出文字说明,证明过程或演算步骤.)
15.设命题p:复数z=(m+1)+(m﹣4)i在复平面上对应的点在第一或第三象限,命题q:方程表示双曲线,若“p且q”为真命题,则求实数m的取值范围.
【分析】分别判断出p,q为真时的m的范围,从而根据p且q”为真命题,得到命题p与命题q均为真命题,从而求出m的范围即可.
【解答】解:∵复数z=(m+1)+(m﹣4)i在复平面上对应的点在第一或第三象限,
∴(m+1)(m﹣4)>0,解得m>4或m<﹣1,
即命题P:m>4或m<﹣1…
∵方程表示双曲线,
∴(1﹣2m)(m+2)<0,解得或m<﹣2,
即命题q:或m<﹣2…
又∵“p且q”为真命题,∴命题p与命题q均为真命题…
则由解得:m>4或m<﹣2,
则所求实数m的取值范围为(﹣∞,﹣2)∪(4,+∞)…
【点评】本题考察了复数和双曲线问题,考察复合命题的判断,是一道基础题.
16.为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
(1)根据江苏省高中学业水平测试要求,成绩低于60分的属于不合格需要补考,求抽取的60名学生中需要补考的学生人数;
(2)根据江苏省高中学业水平测试要求,成绩为60分或高于60分的属于合格,成绩为90分或高于90分的属于优秀,估计本次测试物理学科的合格率和优秀率.
【分析】(1)由各组的频率和等于1,求出成绩低于50分的频率,由此能求出抽取的60名学生中需要补考的学生人数.
(2)求出成绩90及以上的分数所在的第六组的频率,由此能求出估计这次考试物理学科的优秀率;求出成绩为60分及以上的频率,由此能求出估计这次考试物理学科的合格率.
【解答】解:(1)因为各组的频率和等于1,
故成绩低于50分的频率为:1﹣(0.005+2×0.015+0.025+0.03)×10=0.1…
所以低于60分的人数为60×(0.1+0.15)=15(人)
即抽取的60名学生中需要补考的学生人数为15人…
(2)依题意,成绩90及以上的分数所在的第六组(低于50分的为第一组),
频率为0.005×10=0.05,
所以,抽样学生成绩的优秀率是5%,
于是,可以估计这次考试物理学科的优秀率是5%,…
成绩为60分及以上的频率为:f=1﹣(0.1+0.15)=0.75,
即抽样学生成绩的合格率是75%,
于是,可以估计这次考试物理学科的合格率是75%.…
【点评】本题考查频率分布直方图的应用,是基础题,解题时要认真频率分布直方图的性质的合理运用.
17.(1)分别从集合P={﹣2,﹣1,1,2,3}和Q={﹣3,4}中随机抽取一个数依次作为m和n的取值,构成关于x的一次函数y=mx+n,求构成的函数y=mx+n是增函数的概率;
(2)在不等式组所对应的区域内,随机抽取一点A(m,n),以m和n的取值构成关于x的一次函数y=mx+n,求构成的函数y=mx+n的图象经过一、二、四象限的概率.
【分析】(1)本小题是古典概型问题,欲求函数y=mx+n是增函数的概率,只须求出满足:使函数为增函数的事件空间中元素有多少个,再将求得的值与抽取的全部结果的个数求比值即得.
(2)本小题是几何概型问题,欲求函数y=mx+n的图象经过一、二、四象限的概率,只须求出满足使函数图象过一、二、四象限的区域的面积,再将求得的面积值与整个区域的面积求比值即得
【解答】解:(1)由题意可知,抽取的全部结果可表示为(m,n)并且所有基本事件为:(﹣2,﹣3),(﹣2,4),(﹣1,﹣3),(﹣1,4),(1,﹣3),(1,4),(2,﹣3),(2,4),(3,﹣3),(3,4)共10个基本事件,
设使函数为增函数的事件为A,则需满足m>0,故事件A包含的基本事件有:(1,﹣3),(1,4),(2,﹣3),(2,4),(3,﹣3),(3,4),共6个基本事件,
则由古典概型公式得:
即构成的函数y=mx+n是增函数的概率为,
(2)m和n满足的不等式组所对应的区域如右图:
要使构成的函数y=mx+n的图象经过第一、二、四象限,则需满足:,
此时符合条件的点(m,n)所在的区域为图中第二象限的阴影部分,
由几何概型的概率公式得所求事件的概率为
即构成的函数y=mx+n的图象经过一、二、四象限的概率为.
【点评】本小题主要考查古典概型、几何概型等基础知识.古典概型与几何概型的主要区别在于:几何概型是另一类等可能概型,它与古典概型的区别在于试验的结果不是有限个,几何概型的特点有下面两个:(1)试验中所有可能出现的基本事件有无限多个.(2)每个基本事件出现的可能性相等.
18.如图,在半径为的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
(1)分别写出圆柱的侧面积S和体积V关于x的函数关系式;
(2)当x为何值时,才能使得圆柱的侧面积S最大?
(3)当x为何值时,才能使圆柱的体积V最大?并求出最大值.
【分析】(1)连结OC,由BC,OC,可得OB,设圆柱底面半径为r,由AB为底面圆的周长,可得半径r,运用圆柱的侧面积公式和体积公式,即可得到所求解析式;
(2)运用配方和二次函数的最值求法,可得侧面积S的最大值及x的值;
(3)求出体积函数的导数,可得单调区间和极值,且为最值,及x的值.
【解答】解:(1)连结OC,因为BC=x,.
所以,…
设圆柱底面半径为r,则,
即,…
则…
…
(2),
所以当x2=150时,即时,圆柱的侧面积为S为最大…
(3)∵
∴,由V'=0解得x=10,…
又在x∈(0,10)上V'>0,在上V'<0,
所以在(0,10)上是增函数,在上是减函数,
所以当x=10(m)时,圆柱的体积V的最大值为….
【点评】本题考查圆柱的侧面积和体积的最值的求法,注意运用二次函数的最值求法和由导数求单调区间、极值和最值,考查化简整理的运算能力,属于中档题.
19.如图,已知椭圆C:
=1(a>b>0)的离心率为,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
(1)求椭圆C的方程;
(2)求的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
【分析】(1)依题意,得a=2,,由此能求出椭圆C的方程.
(2)法一:点M与点N关于x轴对称,设M(x1,y1),N(x1,﹣y1),设y1>0.由于点M在椭圆C上,故.由T(﹣2,0),知=,由此能求出圆T的方程.
法二:点M与点N关于x轴对称,故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,由T(﹣2,0),得=,由此能求出圆T的方程.
(3)法一:设P(x0,y0),则直线MP的方程为:,令y=0,得,同理:,…故,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
法二:设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.则直线MP的方程为:,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
【解答】解:(1)依题意,得a=2,,
∴c=,b==1,
故椭圆C的方程为.…
(2)方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,﹣y1),不妨设y1>0.
由于点M在椭圆C上,所以.
(
)
…
由已知T(﹣2,0),则,,
∴
=(x1+2)2﹣
=
=.…
由于﹣2<x1<2,
故当时,取得最小值为.
由(
)式,,故,
又点M在圆T上,代入圆的方程得到.
故圆T的方程为:.…
方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨设sinθ>0,由已知T(﹣2,0),
则
=(2cosθ+2)2﹣sin2θ
=5cos2θ+8cosθ+3
=.…
故当时,取得最小值为,
此时,
又点M在圆T上,代入圆的方程得到.
故圆T的方程为:.
…
(3)方法一:设P(x0,y0),
则直线MP的方程为:,
令y=0,得,
同理:,…
故
(
)
…
又点M与点P在椭圆上,
故,,…
代入(
)式,
得:.
所以|OR||OS|=|xR||xS|=|xRxS|=4为定值.
…
方法二:设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为:,
令y=0,得,
同理:,…
故.
所以|OR||OS|=|xR||xS|=|xRxS|=4为定值.…
【点评】本题考查椭圆的方程和几何性质、圆的方程等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想.
20.已知函数f(x)=lnx,,设F(x)=f(x)+g(x),
(1)当a=2时,求函数F(x)的单调区间;
(2)若函数y=F(x)(x∈(0,1])图象上任意一点P(x0,y0)为切点的切线的斜率记为k,且k≤1恒成立,求实数a的最大值;
(3)是否存在实数m,使得函数的图象与函数的图象恰有三个不同交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
【分析】(1)求出F(x)的导数,通过讨论x的范围,得到函数的单调区间;(2)问题转化为在x0∈(0,1]上恒成立,根据函数恒成立求出即可;
(3)问题转化为方程恰有三个不同的实数根,令G(x)=,通过求导得到G(x)的极大值和极小值,从而判断结论.
【解答】解:(1)∵a=2,∴,
则,…
当﹣x2+x+2>0时,解得0<x<2时,F′(x)>0,
即函数y=F(x)在(0,2)上单调递增,…
当﹣x2+x+2<0时,解得x>2时,F′(x)<0,
即函数y=F(x)在(2,+∞)上单调递减,
则函数y=F(x)的单调递增区间为(0,2),单调递减区间为(2,+∞),…
(2)∵,
∴,…
以函数y=F(x)(x∈(0,1])图象上任意一点P(x0,y0)为切点的切线的斜率为k
则在x0∈(0,1]上恒成立,
即在x0∈(0,1]上恒成立,…
令
当时,,
所以,即所求实数a的最大值为…
(3)∵函数的图象与函数的图象恰有三个不同交点,
∴方程恰有三个不同的实数根,
即方程恰有三个不同的实数根,…
令G(x)=,
则,
由G′(x)>0解得:x>2或0<x<1,由G'(x)<0解得:1<x<2,
所以函数y=G(x)在(0,1)和(2,+∞)上单调递增,在(1,2)上单调递减,…
即当x=1时,函数G(x)的极大值为G(1)=﹣2,
即当x=2时,函数G(x)的极小值为,
则由函数y=G(x)图象的草图可知,当时,
方程恰有三个不同的实数根,
即函数的图象与函数的图象恰有三个不同交点.
…
【点评】本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,是一道综合题.
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)
1.命题“ x<3,x2>9”的否定是 .
2.若复数(其中i为虚数单位,a∈R)的实部和虚部相等,则a= .
3.抛物线的准线方程是 .
4.在校园文化艺术节的比赛中,七位评委老师为某参赛选手打分,打出的分数如“茎叶图”所示,若去掉一个最高分和一个最低分后,则所剩数据的方差为 .
5.某校高一、高二、高三年级分别有学生800名,600名,400名.为了解该校高中学生的牙齿健康状况,按各年级的学生数进行分层抽样,若高一抽取x名学生、高二抽取y名学生、高三抽取40名学生,则x+y= .
6.如图是一个算法流程图,则输出S的值是
7.已知m,n∈N
且n>m,在公比为q的等比数列{an}中,有an=amqn﹣m成立,类似地,在公差为d的等差数列{bn}中,有 成立.
8.设a∈R,则“a=1”是“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”的 条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
9.一只蚂蚁在高为3,两底分别为3和7的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为 .
10.已知曲线y=lnx+2在点P处的切线经过点A(0,1),则此切线的方程为 .
11.若椭圆和双曲线有相同的焦点F1,F2,点P是两条曲线的一个交点,则PF1PF2的值是 .
12.已知g(x)=x3﹣x2﹣x﹣1,若对 x1,x2∈[0,2],都有m≤g(x1)﹣g(x2)成立,则m的最大值为
13.已知函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,则满足f(x)<0的x的取值范围为 .
14.已知椭圆=1(a>b>0)的右焦点为F,其右准线与x轴的交点为A,若在椭圆上存在点P满足PF=AF,则﹣2(lnc﹣lna)的范围是 .
二、解答题:(本大题共6小题,共计90分.请把答案写在答题卡相应的位置上.解答时应写出文字说明,证明过程或演算步骤.)
15.设命题p:复数z=(m+1)+(m﹣4)i在复平面上对应的点在第一或第三象限,命题q:方程表示双曲线,若“p且q”为真命题,则求实数m的取值范围.
16.为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
(1)根据江苏省高中学业水平测试要求,成绩低于60分的属于不合格需要补考,求抽取的60名学生中需要补考的学生人数;
(2)根据江苏省高中学业水平测试要求,成绩为60分或高于60分的属于合格,成绩为90分或高于90分的属于优秀,估计本次测试物理学科的合格率和优秀率.
17.(1)分别从集合P={﹣2,﹣1,1,2,3}和Q={﹣3,4}中随机抽取一个数依次作为m和n的取值,构成关于x的一次函数y=mx+n,求构成的函数y=mx+n是增函数的概率;
(2)在不等式组所对应的区域内,随机抽取一点A(m,n),以m和n的取值构成关于x的一次函数y=mx+n,求构成的函数y=mx+n的图象经过一、二、四象限的概率.
18.如图,在半径为的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
(1)分别写出圆柱的侧面积S和体积V关于x的函数关系式;
(2)当x为何值时,才能使得圆柱的侧面积S最大?
(3)当x为何值时,才能使圆柱的体积V最大?并求出最大值.
19.如图,已知椭圆C:
=1(a>b>0)的离心率为,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
(1)求椭圆C的方程;
(2)求的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
20.已知函数f(x)=lnx,,设F(x)=f(x)+g(x),
(1)当a=2时,求函数F(x)的单调区间;
(2)若函数y=F(x)(x∈(0,1])图象上任意一点P(x0,y0)为切点的切线的斜率记为k,且k≤1恒成立,求实数a的最大值;
(3)是否存在实数m,使得函数的图象与函数的图象恰有三个不同交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
2015-2016学年江苏省常州市武进区高二(上)期末数学试卷(文科)
参考答案与试题解析
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)
1.命题“ x<3,x2>9”的否定是 x<3,x2≤9 .
【分析】直接利用特称命题的否定是全称命题写出结果即可.
【解答】解:因为特称命题的否定是全称命题,所以命题“ x<3,x2>9”的否定是: x<3,x2≤9,
故答案为: x<3,x2≤9.
【点评】本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.
2.若复数(其中i为虚数单位,a∈R)的实部和虚部相等,则a= 3 .
【分析】直接由复数代数形式的乘除运算化简复数z,又由复数z的实部和虚部相等,则a可求.
【解答】解:∵
=,
又复数(其中i为虚数单位,a∈R)的实部和虚部相等,
∴﹣a=﹣3即a=3.
故答案为:3.
【点评】本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.
3.抛物线的准线方程是 y=﹣2 .
【分析】将抛物线的方程化为标准方程,再由x2=2py的准线方程y=﹣,即可得到所求方程.
【解答】解:抛物线,即为
x2=8y,即有2p=8,
可得﹣=﹣2.
则准线方程为y=﹣2.
故答案为:y=﹣2.
【点评】本题考查抛物线的准线方程的求法,考查运算能力,属于基础题.
4.在校园文化艺术节的比赛中,七位评委老师为某参赛选手打分,打出的分数如“茎叶图”所示,若去掉一个最高分和一个最低分后,则所剩数据的方差为 .
【分析】根据题意,计算去掉一个最高分和一个最低分后的平均数与方差即可.
【解答】解:根据茎叶图中的数据,计算去掉一个最高分93,一个最低分79后,
所剩数据的平均数是=×(84+84+86+84+87)=85,
方差是s2=×[(84﹣85)2×3+(86﹣85)2+(87﹣85)2]=.
故答案为:.
【点评】本题考查了利用茎叶图中的数据计算平均数与方差的应用问题,是基础题目.
5.某校高一、高二、高三年级分别有学生800名,600名,400名.为了解该校高中学生的牙齿健康状况,按各年级的学生数进行分层抽样,若高一抽取x名学生、高二抽取y名学生、高三抽取40名学生,则x+y= 140 .
【分析】根据分层抽样的定义,建立比例关系,即可得到结论.
【解答】解:∵高一、高二、高三分别有学生800名,600名,400名,
∴若高三抽取40名学生,设共需抽取的学生数为m,
则=,解得m=180,
则高一、高二共需抽取的学生数为x+y=180﹣40=140,
故答案为:140.
【点评】本题主要考查分层抽样的应用,比较基础.
6.如图是一个算法流程图,则输出S的值是 66 .
【分析】模拟程序框图的运行过程,即可得出输出的S值.
【解答】解:第1次循环得S=0+1=1,k=4,此时不满足判断框的条件,
第2次循环得S=1+42=17,k=7,此时不满足判断框的条件,
第3次循环得S=17+72,k=10,此时满足判断框的条件,
输出S=66,结束程序.
故答案为:66.
【点评】本题考查了程序框图的应用问题,解题时应模拟程序语言的运行过程,是基础题目.
7.已知m,n∈N
且n>m,在公比为q的等比数列{an}中,有an=amqn﹣m成立,类似地,在公差为d的等差数列{bn}中,有 bn=bm+(n﹣m)d 成立.
【分析】等差数列{an}中,给出第m项bm和公差,求出首项,再把首项代入等差数列的通项公式中,即可得到结论.
【解答】解:在公差为d的等差数列{bn}中,设其首项为b1,则bm=b1+(m﹣1)d,
∴b1=bm+(1﹣m)d,
则bn=b1+(n﹣1)d=bm+(n﹣m)d,
故答案为:bn=bm+(n﹣m)d.
【点评】本题考查了类比推理,类比推理就是根据两个不同的对象在某些方面的相似之处,从而推出这两个对象在其他方面的也具有的相似之处,是基础题.
8.设a∈R,则“a=1”是“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”的 充分不必要 条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
【分析】利用a=1判断两条直线是否平行;通过两条直线平行是否推出a=1,即可得到答案.
【解答】解:因为“a=1”时,“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0”
化为l1:x+2y﹣1=0与l2:x+2y+4=0,显然两条直线平行;
如果“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”
必有a(a+1)=2,解得a=1或a=﹣2,
所以“a=1”是“直线l1:ax+2y﹣1=0与l2:x+(a+1)y+4=0平行”的充分不必要条件.
故答案为:充分不必要.
【点评】本题考查充要条件的判断,能够正确判断两个命题之间的条件与结论的推出关系是解题的关键.
9.一只蚂蚁在高为3,两底分别为3和7的直角梯形区域内随机爬行,则其恰在离四个顶点距离都大于1的地方的概率为 .
【分析】以四个顶点为圆心,1为半径作圆,当蚂蚁在此区域外的区域随机爬行,离顶点的距离大于1,其面积为15﹣π,再用几何概型公式即得本题的概率
【解答】解:如图由已知,高为3,两底分别为3和7的直角梯形面积为×3×(3+7)=15,
离四个顶点距离都大于1的区域是如图阴影部分,即以四个顶点为圆心,1为半径作圆,当蚂蚁在除此区域外的区域随机爬行,离顶点的距离大于1的部分,其面积为=15﹣π,
∴蚂蚁恰在离四个顶点距离都大于1的地方的概率为P=.
故答案为:.
【点评】本题几何概型的概率.着重考查了图形面积的求法和几何概型的概率求法等知识点,属于基础题.
10.已知曲线y=lnx+2在点P处的切线经过点A(0,1),则此切线的方程为 x﹣y+1=0 .
【分析】设P(m,n),即有n=lnm+2,求出函数的导数,求得切线的斜率,再由两点的斜率公式,解方程可得m=1,再由斜截式方程可得切线的方程.
【解答】解:设P(m,n),即有n=lnm+2,
y=lnx+2的导数为y′=,
即有切线的斜率为k=,
由题意可得=,
解得m=1,n=2,
即有切线的方程为y=x+1.
即为x﹣y+1=0.
故答案为:x﹣y+1=0.
【点评】本题考查导数的运用:求切线的方程,正确求导和运用直线的斜率公式是解题的关键,属于基础题.
11.若椭圆和双曲线有相同的焦点F1,F2,点P是两条曲线的一个交点,则PF1PF2的值是 16 .
【分析】根据点P为椭圆和双曲线的一个交点,结合椭圆和双曲线的第一定义求出|PF1|与|PF2|的表达式,解方程,即可求出|PF1||PF2|的值.
【解答】解:因为椭圆和双曲线有相同的焦点F1,F2,
设P在双曲线的右支上,
利用椭圆以及双曲线的定义可得:|PF1|+|PF2|=2×5=10①
|PF1|﹣|PF2|=2×3=6②
由①②得:|PF1|=8,|PF2|=2.
∴|PF1||PF2|=16.
故答案为:16.
【点评】本题主要考查圆锥曲线的定义、方程和性质,解决本题的关键在于根据椭圆与双曲线有共同的焦点,运用第一定义,考查运算能力,属中档题.
12.已知g(x)=x3﹣x2﹣x﹣1,若对 x1,x2∈[0,2],都有m≤g(x1)﹣g(x2)成立,则m的最大值为 ﹣3 .
【分析】问题转化为m≤g(x)min﹣g(x)max,求出函数g(x)的最大值和最小值,代入求出即可.
【解答】解:g′(x)=3x2﹣2x﹣1=(2x+1)(x﹣1),
令g′(x)>0,解得:x>1,
令g′(x)<0,解得:x<1,
∴g(x)在[0,1)递减,在(1,2]递增;
∴g(x)min=g(1)=﹣2,g(x)max=g(2)=1,
∴m≤g(x)min﹣g(x)max=﹣3,
故答案为:﹣3.
【点评】本题考察了求函数的最值问题,是一道中档题.
13.已知函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,则满足f(x)<0的x的取值范围为 (1,e) .
【分析】求f(x)的导数,利用导数性质能求出满足f(x)<0的x的取值范围.
【解答】解:∵函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,
∴=0,得x=e﹣1,
又f(1)=0,f(e)=0,1<e﹣1<e,
∴由f(x)<0得:1<x<e.
故答案为:(1,e),
【点评】本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意导数性质的合理运用.
14.已知椭圆=1(a>b>0)的右焦点为F,其右准线与x轴的交点为A,若在椭圆上存在点P满足PF=AF,则﹣2(lnc﹣lna)的范围是 (1,
+2ln2] .
【分析】求出椭圆的右焦点和右准线,求得AF的长,再由椭圆的性质,可得a﹣c≤|PF|≤a+c,进而得到a≤2c,a,c的关系,令t=(≤t<1),则f(t)=t2﹣2lnt,运用导数判断单调性,即可得到所求范围.
【解答】解:椭圆=1(a>b>0)的右焦点F(c,0),右准线为x=,
由题意|PF|=|AF|=﹣c,
由椭圆的性质可得a﹣c≤|PF|≤a+c,
即有a﹣c≤﹣c≤a+c,
即有c<a+c且a﹣c≤c,
则有a≤2c,
即为≤<1,
则﹣2(lnc﹣lna)=()2﹣2ln,
令t=(≤t<1),
则f(t)=t2﹣2lnt,
由f′(t)=2t﹣<0在[,1)成立,
则有f(t)在[,1]递减,
故f(t)的范围为(1,
+2ln2].
故答案为:(1,
+2ln2].
【点评】本题考查椭圆的方程和性质,主要考查椭圆的准线方程的运用,椭圆上一点到焦点的距离的最值,同时考查导数的运用:判断单调性,属于中档题.
二、解答题:(本大题共6小题,共计90分.请把答案写在答题卡相应的位置上.解答时应写出文字说明,证明过程或演算步骤.)
15.设命题p:复数z=(m+1)+(m﹣4)i在复平面上对应的点在第一或第三象限,命题q:方程表示双曲线,若“p且q”为真命题,则求实数m的取值范围.
【分析】分别判断出p,q为真时的m的范围,从而根据p且q”为真命题,得到命题p与命题q均为真命题,从而求出m的范围即可.
【解答】解:∵复数z=(m+1)+(m﹣4)i在复平面上对应的点在第一或第三象限,
∴(m+1)(m﹣4)>0,解得m>4或m<﹣1,
即命题P:m>4或m<﹣1…
∵方程表示双曲线,
∴(1﹣2m)(m+2)<0,解得或m<﹣2,
即命题q:或m<﹣2…
又∵“p且q”为真命题,∴命题p与命题q均为真命题…
则由解得:m>4或m<﹣2,
则所求实数m的取值范围为(﹣∞,﹣2)∪(4,+∞)…
【点评】本题考察了复数和双曲线问题,考察复合命题的判断,是一道基础题.
16.为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
(1)根据江苏省高中学业水平测试要求,成绩低于60分的属于不合格需要补考,求抽取的60名学生中需要补考的学生人数;
(2)根据江苏省高中学业水平测试要求,成绩为60分或高于60分的属于合格,成绩为90分或高于90分的属于优秀,估计本次测试物理学科的合格率和优秀率.
【分析】(1)由各组的频率和等于1,求出成绩低于50分的频率,由此能求出抽取的60名学生中需要补考的学生人数.
(2)求出成绩90及以上的分数所在的第六组的频率,由此能求出估计这次考试物理学科的优秀率;求出成绩为60分及以上的频率,由此能求出估计这次考试物理学科的合格率.
【解答】解:(1)因为各组的频率和等于1,
故成绩低于50分的频率为:1﹣(0.005+2×0.015+0.025+0.03)×10=0.1…
所以低于60分的人数为60×(0.1+0.15)=15(人)
即抽取的60名学生中需要补考的学生人数为15人…
(2)依题意,成绩90及以上的分数所在的第六组(低于50分的为第一组),
频率为0.005×10=0.05,
所以,抽样学生成绩的优秀率是5%,
于是,可以估计这次考试物理学科的优秀率是5%,…
成绩为60分及以上的频率为:f=1﹣(0.1+0.15)=0.75,
即抽样学生成绩的合格率是75%,
于是,可以估计这次考试物理学科的合格率是75%.…
【点评】本题考查频率分布直方图的应用,是基础题,解题时要认真频率分布直方图的性质的合理运用.
17.(1)分别从集合P={﹣2,﹣1,1,2,3}和Q={﹣3,4}中随机抽取一个数依次作为m和n的取值,构成关于x的一次函数y=mx+n,求构成的函数y=mx+n是增函数的概率;
(2)在不等式组所对应的区域内,随机抽取一点A(m,n),以m和n的取值构成关于x的一次函数y=mx+n,求构成的函数y=mx+n的图象经过一、二、四象限的概率.
【分析】(1)本小题是古典概型问题,欲求函数y=mx+n是增函数的概率,只须求出满足:使函数为增函数的事件空间中元素有多少个,再将求得的值与抽取的全部结果的个数求比值即得.
(2)本小题是几何概型问题,欲求函数y=mx+n的图象经过一、二、四象限的概率,只须求出满足使函数图象过一、二、四象限的区域的面积,再将求得的面积值与整个区域的面积求比值即得
【解答】解:(1)由题意可知,抽取的全部结果可表示为(m,n)并且所有基本事件为:(﹣2,﹣3),(﹣2,4),(﹣1,﹣3),(﹣1,4),(1,﹣3),(1,4),(2,﹣3),(2,4),(3,﹣3),(3,4)共10个基本事件,
设使函数为增函数的事件为A,则需满足m>0,故事件A包含的基本事件有:(1,﹣3),(1,4),(2,﹣3),(2,4),(3,﹣3),(3,4),共6个基本事件,
则由古典概型公式得:
即构成的函数y=mx+n是增函数的概率为,
(2)m和n满足的不等式组所对应的区域如右图:
要使构成的函数y=mx+n的图象经过第一、二、四象限,则需满足:,
此时符合条件的点(m,n)所在的区域为图中第二象限的阴影部分,
由几何概型的概率公式得所求事件的概率为
即构成的函数y=mx+n的图象经过一、二、四象限的概率为.
【点评】本小题主要考查古典概型、几何概型等基础知识.古典概型与几何概型的主要区别在于:几何概型是另一类等可能概型,它与古典概型的区别在于试验的结果不是有限个,几何概型的特点有下面两个:(1)试验中所有可能出现的基本事件有无限多个.(2)每个基本事件出现的可能性相等.
18.如图,在半径为的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
(1)分别写出圆柱的侧面积S和体积V关于x的函数关系式;
(2)当x为何值时,才能使得圆柱的侧面积S最大?
(3)当x为何值时,才能使圆柱的体积V最大?并求出最大值.
【分析】(1)连结OC,由BC,OC,可得OB,设圆柱底面半径为r,由AB为底面圆的周长,可得半径r,运用圆柱的侧面积公式和体积公式,即可得到所求解析式;
(2)运用配方和二次函数的最值求法,可得侧面积S的最大值及x的值;
(3)求出体积函数的导数,可得单调区间和极值,且为最值,及x的值.
【解答】解:(1)连结OC,因为BC=x,.
所以,…
设圆柱底面半径为r,则,
即,…
则…
…
(2),
所以当x2=150时,即时,圆柱的侧面积为S为最大…
(3)∵
∴,由V'=0解得x=10,…
又在x∈(0,10)上V'>0,在上V'<0,
所以在(0,10)上是增函数,在上是减函数,
所以当x=10(m)时,圆柱的体积V的最大值为….
【点评】本题考查圆柱的侧面积和体积的最值的求法,注意运用二次函数的最值求法和由导数求单调区间、极值和最值,考查化简整理的运算能力,属于中档题.
19.如图,已知椭圆C:
=1(a>b>0)的离心率为,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
(1)求椭圆C的方程;
(2)求的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
【分析】(1)依题意,得a=2,,由此能求出椭圆C的方程.
(2)法一:点M与点N关于x轴对称,设M(x1,y1),N(x1,﹣y1),设y1>0.由于点M在椭圆C上,故.由T(﹣2,0),知=,由此能求出圆T的方程.
法二:点M与点N关于x轴对称,故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,由T(﹣2,0),得=,由此能求出圆T的方程.
(3)法一:设P(x0,y0),则直线MP的方程为:,令y=0,得,同理:,…故,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
法二:设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.则直线MP的方程为:,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
【解答】解:(1)依题意,得a=2,,
∴c=,b==1,
故椭圆C的方程为.…
(2)方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,﹣y1),不妨设y1>0.
由于点M在椭圆C上,所以.
(
)
…
由已知T(﹣2,0),则,,
∴
=(x1+2)2﹣
=
=.…
由于﹣2<x1<2,
故当时,取得最小值为.
由(
)式,,故,
又点M在圆T上,代入圆的方程得到.
故圆T的方程为:.…
方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨设sinθ>0,由已知T(﹣2,0),
则
=(2cosθ+2)2﹣sin2θ
=5cos2θ+8cosθ+3
=.…
故当时,取得最小值为,
此时,
又点M在圆T上,代入圆的方程得到.
故圆T的方程为:.
…
(3)方法一:设P(x0,y0),
则直线MP的方程为:,
令y=0,得,
同理:,…
故
(
)
…
又点M与点P在椭圆上,
故,,…
代入(
)式,
得:.
所以|OR||OS|=|xR||xS|=|xRxS|=4为定值.
…
方法二:设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为:,
令y=0,得,
同理:,…
故.
所以|OR||OS|=|xR||xS|=|xRxS|=4为定值.…
【点评】本题考查椭圆的方程和几何性质、圆的方程等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想.
20.已知函数f(x)=lnx,,设F(x)=f(x)+g(x),
(1)当a=2时,求函数F(x)的单调区间;
(2)若函数y=F(x)(x∈(0,1])图象上任意一点P(x0,y0)为切点的切线的斜率记为k,且k≤1恒成立,求实数a的最大值;
(3)是否存在实数m,使得函数的图象与函数的图象恰有三个不同交点?若存在,求出实数m的取值范围;若不存在,请说明理由.
【分析】(1)求出F(x)的导数,通过讨论x的范围,得到函数的单调区间;(2)问题转化为在x0∈(0,1]上恒成立,根据函数恒成立求出即可;
(3)问题转化为方程恰有三个不同的实数根,令G(x)=,通过求导得到G(x)的极大值和极小值,从而判断结论.
【解答】解:(1)∵a=2,∴,
则,…
当﹣x2+x+2>0时,解得0<x<2时,F′(x)>0,
即函数y=F(x)在(0,2)上单调递增,…
当﹣x2+x+2<0时,解得x>2时,F′(x)<0,
即函数y=F(x)在(2,+∞)上单调递减,
则函数y=F(x)的单调递增区间为(0,2),单调递减区间为(2,+∞),…
(2)∵,
∴,…
以函数y=F(x)(x∈(0,1])图象上任意一点P(x0,y0)为切点的切线的斜率为k
则在x0∈(0,1]上恒成立,
即在x0∈(0,1]上恒成立,…
令
当时,,
所以,即所求实数a的最大值为…
(3)∵函数的图象与函数的图象恰有三个不同交点,
∴方程恰有三个不同的实数根,
即方程恰有三个不同的实数根,…
令G(x)=,
则,
由G′(x)>0解得:x>2或0<x<1,由G'(x)<0解得:1<x<2,
所以函数y=G(x)在(0,1)和(2,+∞)上单调递增,在(1,2)上单调递减,…
即当x=1时,函数G(x)的极大值为G(1)=﹣2,
即当x=2时,函数G(x)的极小值为,
则由函数y=G(x)图象的草图可知,当时,
方程恰有三个不同的实数根,
即函数的图象与函数的图象恰有三个不同交点.
…
【点评】本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,是一道综合题.
同课章节目录
