江西省赣州市瑞金一中2015-2016学年高二(下)周练物理试卷(1)(解析版)
文档属性
| 名称 | 江西省赣州市瑞金一中2015-2016学年高二(下)周练物理试卷(1)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-09-10 20:00:29 | ||
图片预览




文档简介
2015-2016学年江西省赣州市瑞金一中高二(下)周练物理试卷(1)
一、选择题:本题共8小题,每小题6分,在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错的得0分.
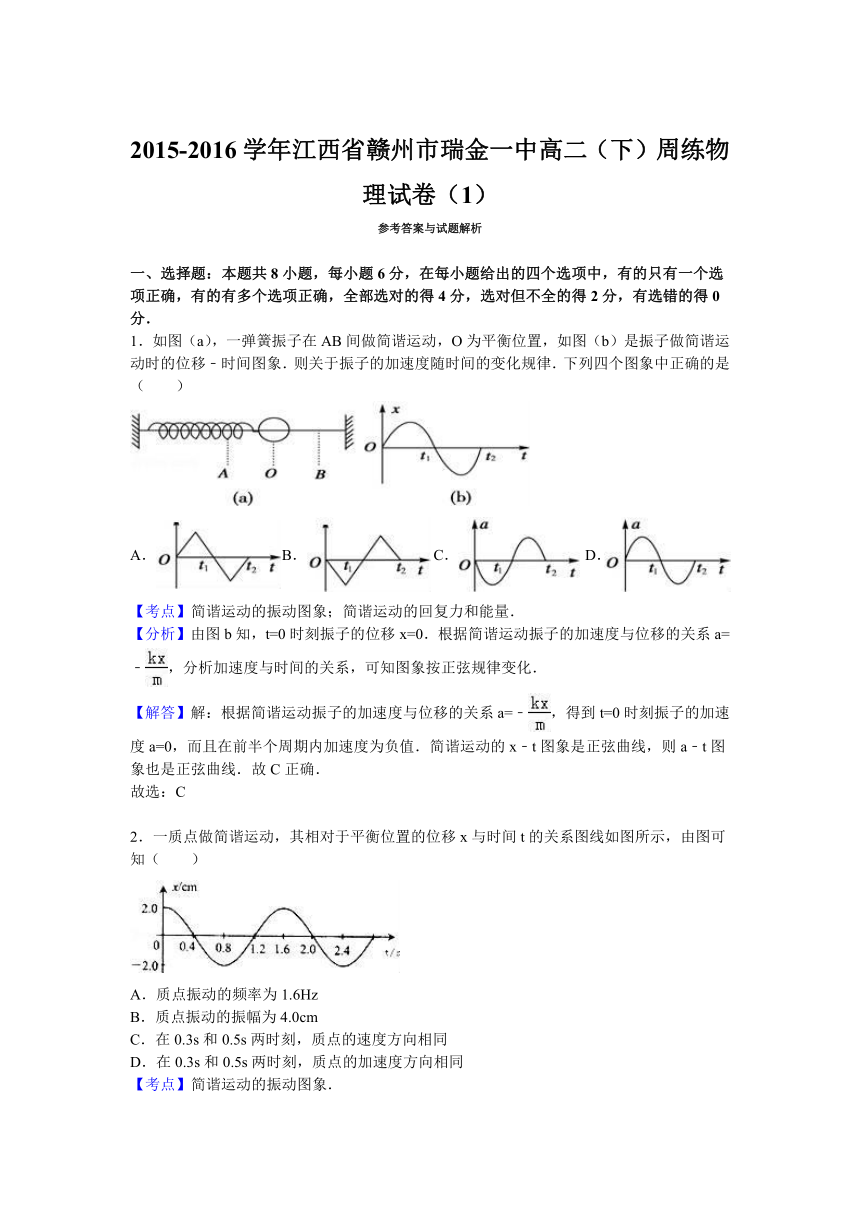
1.如图(a),一弹簧振子在AB间做简谐运动,O为平衡位置,如图(b)是振子做简谐运动时的位移﹣时间图象.则关于振子的加速度随时间的变化规律.下列四个图象中正确的是( )
A.
B.
C.
D.
2.一质点做简谐运动,其相对于平衡位置的位移x与时间t的关系图线如图所示,由图可知( )
A.质点振动的频率为1.6Hz
B.质点振动的振幅为4.0cm
C.在0.3s和0.5s两时刻,质点的速度方向相同
D.在0.3s和0.5s两时刻,质点的加速度方向相同
3.弹簧振子在光滑的水平面上作简谐振动,周期是2.4s.把振子通过平衡位置向右运动时刻记作t=0时刻.有下列说法:①t=1.6s时刻,振子正在向右运动,速度正在变大;②t=1.6s时刻,振子正在向左运动,速度正在变小;③t=1.9s时刻,振子正在向右运动,回复力正在变小;④t=1.9s时刻,振子正在向左运动,回复力正在变大.以上说法中正确的是( )
A.只有①、④正确
B.只有②、③正确
C.只有①、③正确
D.只有②、④正确
4.一弹簧振子做简谐振动,振动图象如图所示,则( )
A.t1、t2时刻振子的速度大小相等,方向相反
B.t1、t2时刻振子加速度大小相等,方向相反
C.t2、t3时刻振子的速度大小相等,方向相反
D.t2、t4时刻振子加速度大小相等,方向相反
5.某质点做简谐运动,从平衡位置开始计时,经过0.5s到达最大位移处,则此简谐运动的周期可能是( )
A.2s
B.
s
C.
s
D.
s
6.计算机光驱的主要部分是激光头,它可以发射脉冲激光信号,激光扫描光盘信息时,激光头利用光敏电阻自动计数器将反射回来的脉冲信号传输给信号处理系统,再通过计算机显示出相应信息.光敏电阻自动计数器的示意图如图所示,其中R1为光敏电阻(在光照下,电阻明显减少),R2为定值电阻,此光电计数器的基本工作原理是( )
A.当有光照射R1时,处理系统获得高电压
B.当有光照射R1时,处理系统获得低电压
C.信号处理系统每获得一次低电压就计数一次
D.信号处理系统每获得一次高电压就计数一次
7.如图所示,R1为定值电阻,R2为负温度系数的热敏电阻(负温度系数热敏电阻是指阻值随温度的升高而减小的热敏电阻),L为小灯泡,当温度降低时( )
A.R1两端的电压增大
B.电流表的示数增大
C.小灯泡的亮度变强
D.小灯泡的亮度变弱
8.有两个振动的振动方程分别是:x1=3sin,x2=5sin,下列说法正确的是( )
A.它们的振幅相同
B.它们的周期相同
C.它们的相差恒定
D.它们的振动步调一致
二、填空题.
9.一个做简谐运动的质点,先后以相同的速度通过a、b两点历时0.1s,再经过0.1s质点第二次(反向)通过b点.若质点在这0.2s内经过的路程是8cm,则此简谐运动的周期为______s,振幅为______cm.
10.将一个水平方向的弹簧振子从它的平衡位置向右拉开10cm,无初速释放,已知振子频率为5Hz,当振子的位移为2cm时,它的加速度大小为4m/s2.则振子在振动过程中的最大加速度为______;振动方程为______.
三、计算题.
11.弹簧振子的固有周期为0.4s,振幅为5cm,从振子经过平衡位置开始计时,经2.5s小球的位置及通过的路程各多大?
12.一物体沿x轴做简谐振动,振幅为8cm,频率为0.5Hz,在t=0时,位移是4cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程表达式并求出t=1s时的位移.
13.如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
(1)当滑块运动到振幅一半时,砝码所受回复力有多大?
(2)当砝码与滑块的动摩擦因数为μ时,要使砝码与滑块不发生相对滑动的最大振幅为多大?
2015-2016学年江西省赣州市瑞金一中高二(下)周练物理试卷(1)
参考答案与试题解析
一、选择题:本题共8小题,每小题6分,在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错的得0分.
1.如图(a),一弹簧振子在AB间做简谐运动,O为平衡位置,如图(b)是振子做简谐运动时的位移﹣时间图象.则关于振子的加速度随时间的变化规律.下列四个图象中正确的是( )
A.
B.
C.
D.
【考点】简谐运动的振动图象;简谐运动的回复力和能量.
【分析】由图b知,t=0时刻振子的位移x=0.根据简谐运动振子的加速度与位移的关系a=﹣,分析加速度与时间的关系,可知图象按正弦规律变化.
【解答】解:根据简谐运动振子的加速度与位移的关系a=﹣,得到t=0时刻振子的加速度a=0,而且在前半个周期内加速度为负值.简谐运动的x﹣t图象是正弦曲线,则a﹣t图象也是正弦曲线.故C正确.
故选:C
2.一质点做简谐运动,其相对于平衡位置的位移x与时间t的关系图线如图所示,由图可知( )
A.质点振动的频率为1.6Hz
B.质点振动的振幅为4.0cm
C.在0.3s和0.5s两时刻,质点的速度方向相同
D.在0.3s和0.5s两时刻,质点的加速度方向相同
【考点】简谐运动的振动图象.
【分析】质点的振幅等于振子的位移最大值,由图直接读出振幅和周期,由公式f=求出频率.根据给定时刻以后质点位移的变化,分析速度的方向,由简谐运动的特征a=﹣分析加速度的方向.
【解答】解:A、由图读出周期T=1.6s,则频率f==0.625Hz.故A错误.
B、质点的振幅等于振子的位移最大值,由图直接读出振幅A=2cm.故B错误.
C、在0.3s时刻,质点正从正向最大位移向平衡位置运动,速度沿负方向;在0.5s时刻,质点正从平衡位置向负向最大位移处运动,速度方向沿负方向,故这两个时刻的速度方向相同.故C正确.
D、由简谐运动的特征a=﹣分析得知,在0.3s和0.5s两时刻,质点的加速度方向相反.故D错误.
故选C
3.弹簧振子在光滑的水平面上作简谐振动,周期是2.4s.把振子通过平衡位置向右运动时刻记作t=0时刻.有下列说法:①t=1.6s时刻,振子正在向右运动,速度正在变大;②t=1.6s时刻,振子正在向左运动,速度正在变小;③t=1.9s时刻,振子正在向右运动,回复力正在变小;④t=1.9s时刻,振子正在向左运动,回复力正在变大.以上说法中正确的是( )
A.只有①、④正确
B.只有②、③正确
C.只有①、③正确
D.只有②、④正确
【考点】简谐运动的回复力和能量.
【分析】弹簧振子做简谐运动,弹簧的弹力为回复力,根据牛顿第二定律判断加速度的变化,根据加速度方向与速度方向的关系判断速度的变化.
【解答】解:①②振子的周期是2.4s,经过1.6s时,经过了三分之二周期;,此时振子在平衡位置的左侧,向左侧的最大位置运动,弹簧的弹性势能越来越大,振子的动能越来越小,速度将不断变小.故①错误.②正确;
③④经过1.9s时,,此时振子在平衡位置的左侧,向平衡位置运动,振子的位移越来越小,则回复力越来越小.故③正确,④错误.
所以选项D正确
故选:D
4.一弹簧振子做简谐振动,振动图象如图所示,则( )
A.t1、t2时刻振子的速度大小相等,方向相反
B.t1、t2时刻振子加速度大小相等,方向相反
C.t2、t3时刻振子的速度大小相等,方向相反
D.t2、t4时刻振子加速度大小相等,方向相反
【考点】简谐运动的回复力和能量;简谐运动的振幅、周期和频率.
【分析】简谐运动中,回复力F=﹣kx,加速度a=﹣;x﹣t图象的切线的斜率表示速度.
【解答】解:A、t1、t2时刻,x﹣t图象的切线斜率等大反向,故振子的速度大小相等、方向相反,故A正确;
B、t1、t2时刻振子的位移相同,故加速度a=﹣也相同,故B错误;
C、t2、t3时刻,x﹣t图象的切线斜率相同,故振子的速度大小相等、方向相同,故C错误;
D、t2、t4时刻振子的位移等大反向,故加速度a=﹣也等大反向,故D正确;
故选:AD.
5.某质点做简谐运动,从平衡位置开始计时,经过0.5s到达最大位移处,则此简谐运动的周期可能是( )
A.2s
B.
s
C.
s
D.
s
【考点】简谐运动的振幅、周期和频率.
【分析】振子开始运动的方向可能先向右,也可能向左,画出振子的运动过程示意图,确定振动周期.
【解答】解:如图所示
质点完成
所以质点的周期T=4×0.5s=2s
如图所示:
质点完成次全振动的时间为0.5s,
所以质点的周期T=0.5×=s.
故选:AB.
6.计算机光驱的主要部分是激光头,它可以发射脉冲激光信号,激光扫描光盘信息时,激光头利用光敏电阻自动计数器将反射回来的脉冲信号传输给信号处理系统,再通过计算机显示出相应信息.光敏电阻自动计数器的示意图如图所示,其中R1为光敏电阻(在光照下,电阻明显减少),R2为定值电阻,此光电计数器的基本工作原理是( )
A.当有光照射R1时,处理系统获得高电压
B.当有光照射R1时,处理系统获得低电压
C.信号处理系统每获得一次低电压就计数一次
D.信号处理系统每获得一次高电压就计数一次
【考点】简单的逻辑电路.
【分析】由图可知,电阻R1与R2串联,当R1的电阻值受光照亮度的增大而减小时,根据欧姆定律可知,电路中的电流增大,由于R2阻值一定,根据U2=IR2可知,AB间电压增大,反之减小;根据串联电路的电压特点可知R1两端的电压的变化.可据此分析判断.
【解答】解:由题知,当光线照射R1时,R1阻值减小、R总减小,由欧姆定律得:I=且电源电压不变,
∴电路中的电流增大,
∵R2是定值电阻,U2=IR2,
∴R2两端电压增大,信号处理系统获得高压而计数,
∵串联电路总电压等于各分电压之和,
∴R1两端的电压变小,故A正确、B错;
当光线照射时,R1阻值增小、R总增小,电路中的电流减大,R2两端电压变大,
所以信号处理系统每获得一次高电压就计数一次,故C错.D正确
故选AD.
7.如图所示,R1为定值电阻,R2为负温度系数的热敏电阻(负温度系数热敏电阻是指阻值随温度的升高而减小的热敏电阻),L为小灯泡,当温度降低时( )
A.R1两端的电压增大
B.电流表的示数增大
C.小灯泡的亮度变强
D.小灯泡的亮度变弱
【考点】闭合电路的欧姆定律.
【分析】由图可知,R2和灯泡并联后与R1串联,电流表测量干路电流;负温度系数的热敏电阻的特性:温度升高,电阻减小.根据温度下降时,R2电阻增大,确定并联部分电阻及总电阻的变化情况,可定出电流、电压的变化情况及灯泡亮度变化情况.
【解答】解:AB、温度降低时,R2电阻增大,并联部分电阻增大,总电阻增大,总电流减小,则R1电压减小,电流表示数减小.故A、B错误.
CD、因为内电压和R1两端电压减小,根据串联电路电压特点可知,灯泡的电压增大,故灯泡变亮.故C正确,D错误.
故选:C
8.有两个振动的振动方程分别是:x1=3sin,x2=5sin,下列说法正确的是( )
A.它们的振幅相同
B.它们的周期相同
C.它们的相差恒定
D.它们的振动步调一致
【考点】简谐运动的振幅、周期和频率.
【分析】根据两个简谐运动的振动方程读出位移大小的最大值,即为振幅,读出角速度,求出周期.读出相位,求出其差,分析步调关系.
【解答】解:
A、由题,第一简谐运动的振幅为A1=3,第二简谐运动的振幅也为A2=5,所以它们的振幅不相同.故A错误.
B、第一简谐运动的角速度为ω1=100πrad/s,其周期为T1==0.02s,第二简谐运动的角速度为ω2=100πrad/s,其周期为T2==0.02s,周期相同.故B正确.
C、第一简谐运动的相位为φ1=100π+,第二简谐运动的相位为φ2=100π+,相差为△φ=φ2﹣φ1=,恒定不变.故C正确.
D、由上看出,两个简谐运动存在相位差,步调不一致.故D错误.
故选:BC
二、填空题.
9.一个做简谐运动的质点,先后以相同的速度通过a、b两点历时0.1s,再经过0.1s质点第二次(反向)通过b点.若质点在这0.2s内经过的路程是8cm,则此简谐运动的周期为 0.4 s,振幅为 4 cm.
【考点】简谐运动的振幅、周期和频率.
【分析】简谐运动的质点,先后以同样大小的速度通过a、b两点,则可判定这两点关于平衡位置对称,则平衡位置到b点的时间为0.1秒的一半;由当再次经过b点的时间,即可求出从b点到最大位置的时间为0.1秒的一半,因此质点的振动同期为平衡位置到最大位置时间的4倍.
【解答】解:简谐运动的质点,先后以同样大小的速度通过a、b两点,则可判定这两点关于平衡位置O点对称,所以质点由a到O时间与由O到b的时间相等.
由于再经过0.1s质点第二次(反向)通过b点,说明开始时,由a向0运动的过程中,运动的方向是a指向0点,所以该过程恰好是半个周期,则此简谐运动的周期为T=2(t1+t2)=2×(0.1+0.1)=0.4s;
质点在半个周期内的位移是2倍在振幅,所以该振动的振幅是:A=×8cm=4cm
故答案为:0.4,4
10.将一个水平方向的弹簧振子从它的平衡位置向右拉开10cm,无初速释放,已知振子频率为5Hz,当振子的位移为2cm时,它的加速度大小为4m/s2.则振子在振动过程中的最大加速度为 20m/s2 ;振动方程为 y=﹣0.1sin10πt .
【考点】简谐运动的回复力和能量.
【分析】根据胡克定律结合牛顿第二定律即可求出振子的最大加速度;根据振幅与频率即可写出振动方程即可.
【解答】解:由题振子的振幅为:A=10cm=0.1m
设振子的质量为m,当位移为2cm时:kx1=ma1
当位移为10cm时:kx2=ma2
联立得:a=20m/s2
振子的频率为10Hz,则ω=2πf=2π×5=10π
rad/s
振子的振动方程为y=﹣Asinωt=﹣0.1sin10πt
故答案为:20m/s2,y=﹣0.1sin10πt
三、计算题.
11.弹簧振子的固有周期为0.4s,振幅为5cm,从振子经过平衡位置开始计时,经2.5s小球的位置及通过的路程各多大?
【考点】简谐运动的振幅、周期和频率.
【分析】根据振子在一个周期内通过的路程是四个振幅,求出振子在2.5s内通过的路程,确定振子的位置,求出位移的大小.
【解答】解:时间t=2.5s=6T+,由于从平衡位置开始振动,所以在2.5s内振子通过的路程为S=25A=25×0.05cm=1.25m
经过2.5s,振子到达最大位移处,其位移大小为:x=A=0.05m.
答:经2.5s小球的位置在最大位移处,及通过的路程1.25m.
12.一物体沿x轴做简谐振动,振幅为8cm,频率为0.5Hz,在t=0时,位移是4cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程表达式并求出t=1s时的位移.
【考点】简谐运动的振动图象;简谐运动的振幅、周期和频率.
【分析】简谐运动振动方程的一般表达式x=Asin(ωt+φ),将在t=0时,位移是4cm代入即可求解.
【解答】解:简谐运动振动方程的一般表达式x=Asin(ωt+φ)
由题得:A=0.08m,ω=2πf=π
所以x=0.08sin(πt+φ)m
将t=0时x=0.04m代入得0.04=0.08sinφ,
解得初相或.
在为t=0时,速度方向沿x轴负方向,即位移在减小,所以取
所求的振动方向为
当t=1s时,代入上述表达式得x=﹣0.04m,即t=1s时振动物体的位移大小为0.04m,方向为x轴负向.
答:振动方程表达式为,t=1s时的位移为﹣0.04m.
13.如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
(1)当滑块运动到振幅一半时,砝码所受回复力有多大?
(2)当砝码与滑块的动摩擦因数为μ时,要使砝码与滑块不发生相对滑动的最大振幅为多大?
【考点】简谐运动的回复力和能量;牛顿第二定律.
【分析】(1)滑块的回复力是由静摩擦力提供,根据牛顿第二定律,结合胡克定律和形变量的大小,即可求解;
(2)根据x增大时,f也增大,结合最大静摩擦力等于滑动摩擦力,即可求解.
【解答】解:(1)使砝码随着滑块一起振动,砝码所受静摩擦力是产生砝码与滑块一起变加速运动的加速度.故M对m的静摩擦力是回复力.
其大小由牛顿第二定律有:f=ma
整体法求共同加速度a,则有:a=;
当滑块运动到振动幅的一半位置时回复力:
=,方向指向平衡位置.
(2)从f=k′x,可以看出,当x增大时,f也增大,当f=fmax=μN时,有最大振动幅,
因fm=mam=μmg
所以:;
解得:Am=;
答:(1)当滑块运动到振幅一半时,砝码所受回复力有,方向指向平衡位置;
(2)当砝码与滑块的动摩擦因数为μ时,要使砝码与滑块不发生相对滑动的最大振幅为.
2016年9月10日
一、选择题:本题共8小题,每小题6分,在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错的得0分.
1.如图(a),一弹簧振子在AB间做简谐运动,O为平衡位置,如图(b)是振子做简谐运动时的位移﹣时间图象.则关于振子的加速度随时间的变化规律.下列四个图象中正确的是( )
A.
B.
C.
D.
2.一质点做简谐运动,其相对于平衡位置的位移x与时间t的关系图线如图所示,由图可知( )
A.质点振动的频率为1.6Hz
B.质点振动的振幅为4.0cm
C.在0.3s和0.5s两时刻,质点的速度方向相同
D.在0.3s和0.5s两时刻,质点的加速度方向相同
3.弹簧振子在光滑的水平面上作简谐振动,周期是2.4s.把振子通过平衡位置向右运动时刻记作t=0时刻.有下列说法:①t=1.6s时刻,振子正在向右运动,速度正在变大;②t=1.6s时刻,振子正在向左运动,速度正在变小;③t=1.9s时刻,振子正在向右运动,回复力正在变小;④t=1.9s时刻,振子正在向左运动,回复力正在变大.以上说法中正确的是( )
A.只有①、④正确
B.只有②、③正确
C.只有①、③正确
D.只有②、④正确
4.一弹簧振子做简谐振动,振动图象如图所示,则( )
A.t1、t2时刻振子的速度大小相等,方向相反
B.t1、t2时刻振子加速度大小相等,方向相反
C.t2、t3时刻振子的速度大小相等,方向相反
D.t2、t4时刻振子加速度大小相等,方向相反
5.某质点做简谐运动,从平衡位置开始计时,经过0.5s到达最大位移处,则此简谐运动的周期可能是( )
A.2s
B.
s
C.
s
D.
s
6.计算机光驱的主要部分是激光头,它可以发射脉冲激光信号,激光扫描光盘信息时,激光头利用光敏电阻自动计数器将反射回来的脉冲信号传输给信号处理系统,再通过计算机显示出相应信息.光敏电阻自动计数器的示意图如图所示,其中R1为光敏电阻(在光照下,电阻明显减少),R2为定值电阻,此光电计数器的基本工作原理是( )
A.当有光照射R1时,处理系统获得高电压
B.当有光照射R1时,处理系统获得低电压
C.信号处理系统每获得一次低电压就计数一次
D.信号处理系统每获得一次高电压就计数一次
7.如图所示,R1为定值电阻,R2为负温度系数的热敏电阻(负温度系数热敏电阻是指阻值随温度的升高而减小的热敏电阻),L为小灯泡,当温度降低时( )
A.R1两端的电压增大
B.电流表的示数增大
C.小灯泡的亮度变强
D.小灯泡的亮度变弱
8.有两个振动的振动方程分别是:x1=3sin,x2=5sin,下列说法正确的是( )
A.它们的振幅相同
B.它们的周期相同
C.它们的相差恒定
D.它们的振动步调一致
二、填空题.
9.一个做简谐运动的质点,先后以相同的速度通过a、b两点历时0.1s,再经过0.1s质点第二次(反向)通过b点.若质点在这0.2s内经过的路程是8cm,则此简谐运动的周期为______s,振幅为______cm.
10.将一个水平方向的弹簧振子从它的平衡位置向右拉开10cm,无初速释放,已知振子频率为5Hz,当振子的位移为2cm时,它的加速度大小为4m/s2.则振子在振动过程中的最大加速度为______;振动方程为______.
三、计算题.
11.弹簧振子的固有周期为0.4s,振幅为5cm,从振子经过平衡位置开始计时,经2.5s小球的位置及通过的路程各多大?
12.一物体沿x轴做简谐振动,振幅为8cm,频率为0.5Hz,在t=0时,位移是4cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程表达式并求出t=1s时的位移.
13.如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
(1)当滑块运动到振幅一半时,砝码所受回复力有多大?
(2)当砝码与滑块的动摩擦因数为μ时,要使砝码与滑块不发生相对滑动的最大振幅为多大?
2015-2016学年江西省赣州市瑞金一中高二(下)周练物理试卷(1)
参考答案与试题解析
一、选择题:本题共8小题,每小题6分,在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错的得0分.
1.如图(a),一弹簧振子在AB间做简谐运动,O为平衡位置,如图(b)是振子做简谐运动时的位移﹣时间图象.则关于振子的加速度随时间的变化规律.下列四个图象中正确的是( )
A.
B.
C.
D.
【考点】简谐运动的振动图象;简谐运动的回复力和能量.
【分析】由图b知,t=0时刻振子的位移x=0.根据简谐运动振子的加速度与位移的关系a=﹣,分析加速度与时间的关系,可知图象按正弦规律变化.
【解答】解:根据简谐运动振子的加速度与位移的关系a=﹣,得到t=0时刻振子的加速度a=0,而且在前半个周期内加速度为负值.简谐运动的x﹣t图象是正弦曲线,则a﹣t图象也是正弦曲线.故C正确.
故选:C
2.一质点做简谐运动,其相对于平衡位置的位移x与时间t的关系图线如图所示,由图可知( )
A.质点振动的频率为1.6Hz
B.质点振动的振幅为4.0cm
C.在0.3s和0.5s两时刻,质点的速度方向相同
D.在0.3s和0.5s两时刻,质点的加速度方向相同
【考点】简谐运动的振动图象.
【分析】质点的振幅等于振子的位移最大值,由图直接读出振幅和周期,由公式f=求出频率.根据给定时刻以后质点位移的变化,分析速度的方向,由简谐运动的特征a=﹣分析加速度的方向.
【解答】解:A、由图读出周期T=1.6s,则频率f==0.625Hz.故A错误.
B、质点的振幅等于振子的位移最大值,由图直接读出振幅A=2cm.故B错误.
C、在0.3s时刻,质点正从正向最大位移向平衡位置运动,速度沿负方向;在0.5s时刻,质点正从平衡位置向负向最大位移处运动,速度方向沿负方向,故这两个时刻的速度方向相同.故C正确.
D、由简谐运动的特征a=﹣分析得知,在0.3s和0.5s两时刻,质点的加速度方向相反.故D错误.
故选C
3.弹簧振子在光滑的水平面上作简谐振动,周期是2.4s.把振子通过平衡位置向右运动时刻记作t=0时刻.有下列说法:①t=1.6s时刻,振子正在向右运动,速度正在变大;②t=1.6s时刻,振子正在向左运动,速度正在变小;③t=1.9s时刻,振子正在向右运动,回复力正在变小;④t=1.9s时刻,振子正在向左运动,回复力正在变大.以上说法中正确的是( )
A.只有①、④正确
B.只有②、③正确
C.只有①、③正确
D.只有②、④正确
【考点】简谐运动的回复力和能量.
【分析】弹簧振子做简谐运动,弹簧的弹力为回复力,根据牛顿第二定律判断加速度的变化,根据加速度方向与速度方向的关系判断速度的变化.
【解答】解:①②振子的周期是2.4s,经过1.6s时,经过了三分之二周期;,此时振子在平衡位置的左侧,向左侧的最大位置运动,弹簧的弹性势能越来越大,振子的动能越来越小,速度将不断变小.故①错误.②正确;
③④经过1.9s时,,此时振子在平衡位置的左侧,向平衡位置运动,振子的位移越来越小,则回复力越来越小.故③正确,④错误.
所以选项D正确
故选:D
4.一弹簧振子做简谐振动,振动图象如图所示,则( )
A.t1、t2时刻振子的速度大小相等,方向相反
B.t1、t2时刻振子加速度大小相等,方向相反
C.t2、t3时刻振子的速度大小相等,方向相反
D.t2、t4时刻振子加速度大小相等,方向相反
【考点】简谐运动的回复力和能量;简谐运动的振幅、周期和频率.
【分析】简谐运动中,回复力F=﹣kx,加速度a=﹣;x﹣t图象的切线的斜率表示速度.
【解答】解:A、t1、t2时刻,x﹣t图象的切线斜率等大反向,故振子的速度大小相等、方向相反,故A正确;
B、t1、t2时刻振子的位移相同,故加速度a=﹣也相同,故B错误;
C、t2、t3时刻,x﹣t图象的切线斜率相同,故振子的速度大小相等、方向相同,故C错误;
D、t2、t4时刻振子的位移等大反向,故加速度a=﹣也等大反向,故D正确;
故选:AD.
5.某质点做简谐运动,从平衡位置开始计时,经过0.5s到达最大位移处,则此简谐运动的周期可能是( )
A.2s
B.
s
C.
s
D.
s
【考点】简谐运动的振幅、周期和频率.
【分析】振子开始运动的方向可能先向右,也可能向左,画出振子的运动过程示意图,确定振动周期.
【解答】解:如图所示
质点完成
所以质点的周期T=4×0.5s=2s
如图所示:
质点完成次全振动的时间为0.5s,
所以质点的周期T=0.5×=s.
故选:AB.
6.计算机光驱的主要部分是激光头,它可以发射脉冲激光信号,激光扫描光盘信息时,激光头利用光敏电阻自动计数器将反射回来的脉冲信号传输给信号处理系统,再通过计算机显示出相应信息.光敏电阻自动计数器的示意图如图所示,其中R1为光敏电阻(在光照下,电阻明显减少),R2为定值电阻,此光电计数器的基本工作原理是( )
A.当有光照射R1时,处理系统获得高电压
B.当有光照射R1时,处理系统获得低电压
C.信号处理系统每获得一次低电压就计数一次
D.信号处理系统每获得一次高电压就计数一次
【考点】简单的逻辑电路.
【分析】由图可知,电阻R1与R2串联,当R1的电阻值受光照亮度的增大而减小时,根据欧姆定律可知,电路中的电流增大,由于R2阻值一定,根据U2=IR2可知,AB间电压增大,反之减小;根据串联电路的电压特点可知R1两端的电压的变化.可据此分析判断.
【解答】解:由题知,当光线照射R1时,R1阻值减小、R总减小,由欧姆定律得:I=且电源电压不变,
∴电路中的电流增大,
∵R2是定值电阻,U2=IR2,
∴R2两端电压增大,信号处理系统获得高压而计数,
∵串联电路总电压等于各分电压之和,
∴R1两端的电压变小,故A正确、B错;
当光线照射时,R1阻值增小、R总增小,电路中的电流减大,R2两端电压变大,
所以信号处理系统每获得一次高电压就计数一次,故C错.D正确
故选AD.
7.如图所示,R1为定值电阻,R2为负温度系数的热敏电阻(负温度系数热敏电阻是指阻值随温度的升高而减小的热敏电阻),L为小灯泡,当温度降低时( )
A.R1两端的电压增大
B.电流表的示数增大
C.小灯泡的亮度变强
D.小灯泡的亮度变弱
【考点】闭合电路的欧姆定律.
【分析】由图可知,R2和灯泡并联后与R1串联,电流表测量干路电流;负温度系数的热敏电阻的特性:温度升高,电阻减小.根据温度下降时,R2电阻增大,确定并联部分电阻及总电阻的变化情况,可定出电流、电压的变化情况及灯泡亮度变化情况.
【解答】解:AB、温度降低时,R2电阻增大,并联部分电阻增大,总电阻增大,总电流减小,则R1电压减小,电流表示数减小.故A、B错误.
CD、因为内电压和R1两端电压减小,根据串联电路电压特点可知,灯泡的电压增大,故灯泡变亮.故C正确,D错误.
故选:C
8.有两个振动的振动方程分别是:x1=3sin,x2=5sin,下列说法正确的是( )
A.它们的振幅相同
B.它们的周期相同
C.它们的相差恒定
D.它们的振动步调一致
【考点】简谐运动的振幅、周期和频率.
【分析】根据两个简谐运动的振动方程读出位移大小的最大值,即为振幅,读出角速度,求出周期.读出相位,求出其差,分析步调关系.
【解答】解:
A、由题,第一简谐运动的振幅为A1=3,第二简谐运动的振幅也为A2=5,所以它们的振幅不相同.故A错误.
B、第一简谐运动的角速度为ω1=100πrad/s,其周期为T1==0.02s,第二简谐运动的角速度为ω2=100πrad/s,其周期为T2==0.02s,周期相同.故B正确.
C、第一简谐运动的相位为φ1=100π+,第二简谐运动的相位为φ2=100π+,相差为△φ=φ2﹣φ1=,恒定不变.故C正确.
D、由上看出,两个简谐运动存在相位差,步调不一致.故D错误.
故选:BC
二、填空题.
9.一个做简谐运动的质点,先后以相同的速度通过a、b两点历时0.1s,再经过0.1s质点第二次(反向)通过b点.若质点在这0.2s内经过的路程是8cm,则此简谐运动的周期为 0.4 s,振幅为 4 cm.
【考点】简谐运动的振幅、周期和频率.
【分析】简谐运动的质点,先后以同样大小的速度通过a、b两点,则可判定这两点关于平衡位置对称,则平衡位置到b点的时间为0.1秒的一半;由当再次经过b点的时间,即可求出从b点到最大位置的时间为0.1秒的一半,因此质点的振动同期为平衡位置到最大位置时间的4倍.
【解答】解:简谐运动的质点,先后以同样大小的速度通过a、b两点,则可判定这两点关于平衡位置O点对称,所以质点由a到O时间与由O到b的时间相等.
由于再经过0.1s质点第二次(反向)通过b点,说明开始时,由a向0运动的过程中,运动的方向是a指向0点,所以该过程恰好是半个周期,则此简谐运动的周期为T=2(t1+t2)=2×(0.1+0.1)=0.4s;
质点在半个周期内的位移是2倍在振幅,所以该振动的振幅是:A=×8cm=4cm
故答案为:0.4,4
10.将一个水平方向的弹簧振子从它的平衡位置向右拉开10cm,无初速释放,已知振子频率为5Hz,当振子的位移为2cm时,它的加速度大小为4m/s2.则振子在振动过程中的最大加速度为 20m/s2 ;振动方程为 y=﹣0.1sin10πt .
【考点】简谐运动的回复力和能量.
【分析】根据胡克定律结合牛顿第二定律即可求出振子的最大加速度;根据振幅与频率即可写出振动方程即可.
【解答】解:由题振子的振幅为:A=10cm=0.1m
设振子的质量为m,当位移为2cm时:kx1=ma1
当位移为10cm时:kx2=ma2
联立得:a=20m/s2
振子的频率为10Hz,则ω=2πf=2π×5=10π
rad/s
振子的振动方程为y=﹣Asinωt=﹣0.1sin10πt
故答案为:20m/s2,y=﹣0.1sin10πt
三、计算题.
11.弹簧振子的固有周期为0.4s,振幅为5cm,从振子经过平衡位置开始计时,经2.5s小球的位置及通过的路程各多大?
【考点】简谐运动的振幅、周期和频率.
【分析】根据振子在一个周期内通过的路程是四个振幅,求出振子在2.5s内通过的路程,确定振子的位置,求出位移的大小.
【解答】解:时间t=2.5s=6T+,由于从平衡位置开始振动,所以在2.5s内振子通过的路程为S=25A=25×0.05cm=1.25m
经过2.5s,振子到达最大位移处,其位移大小为:x=A=0.05m.
答:经2.5s小球的位置在最大位移处,及通过的路程1.25m.
12.一物体沿x轴做简谐振动,振幅为8cm,频率为0.5Hz,在t=0时,位移是4cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程表达式并求出t=1s时的位移.
【考点】简谐运动的振动图象;简谐运动的振幅、周期和频率.
【分析】简谐运动振动方程的一般表达式x=Asin(ωt+φ),将在t=0时,位移是4cm代入即可求解.
【解答】解:简谐运动振动方程的一般表达式x=Asin(ωt+φ)
由题得:A=0.08m,ω=2πf=π
所以x=0.08sin(πt+φ)m
将t=0时x=0.04m代入得0.04=0.08sinφ,
解得初相或.
在为t=0时,速度方向沿x轴负方向,即位移在减小,所以取
所求的振动方向为
当t=1s时,代入上述表达式得x=﹣0.04m,即t=1s时振动物体的位移大小为0.04m,方向为x轴负向.
答:振动方程表达式为,t=1s时的位移为﹣0.04m.
13.如图所示,弹簧振子在光滑水平面上以振幅A做简谐运动,质量为M的滑块上面放一个质量为m的砝码,砝码随滑块一起做简谐运动,已知弹簧的劲度系数为k,试求:
(1)当滑块运动到振幅一半时,砝码所受回复力有多大?
(2)当砝码与滑块的动摩擦因数为μ时,要使砝码与滑块不发生相对滑动的最大振幅为多大?
【考点】简谐运动的回复力和能量;牛顿第二定律.
【分析】(1)滑块的回复力是由静摩擦力提供,根据牛顿第二定律,结合胡克定律和形变量的大小,即可求解;
(2)根据x增大时,f也增大,结合最大静摩擦力等于滑动摩擦力,即可求解.
【解答】解:(1)使砝码随着滑块一起振动,砝码所受静摩擦力是产生砝码与滑块一起变加速运动的加速度.故M对m的静摩擦力是回复力.
其大小由牛顿第二定律有:f=ma
整体法求共同加速度a,则有:a=;
当滑块运动到振动幅的一半位置时回复力:
=,方向指向平衡位置.
(2)从f=k′x,可以看出,当x增大时,f也增大,当f=fmax=μN时,有最大振动幅,
因fm=mam=μmg
所以:;
解得:Am=;
答:(1)当滑块运动到振幅一半时,砝码所受回复力有,方向指向平衡位置;
(2)当砝码与滑块的动摩擦因数为μ时,要使砝码与滑块不发生相对滑动的最大振幅为.
2016年9月10日
