椭圆的简单几何性质
图片预览



文档简介
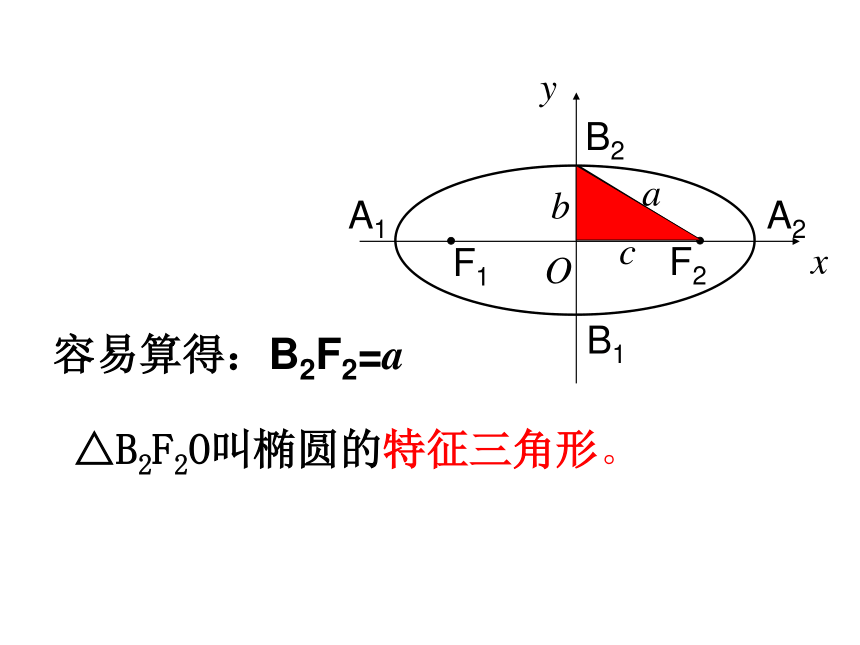
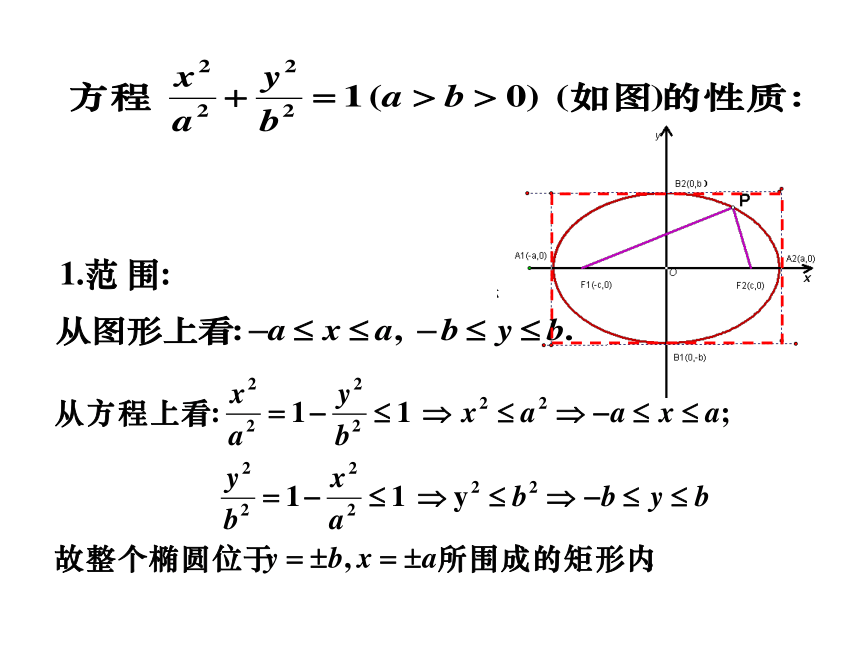
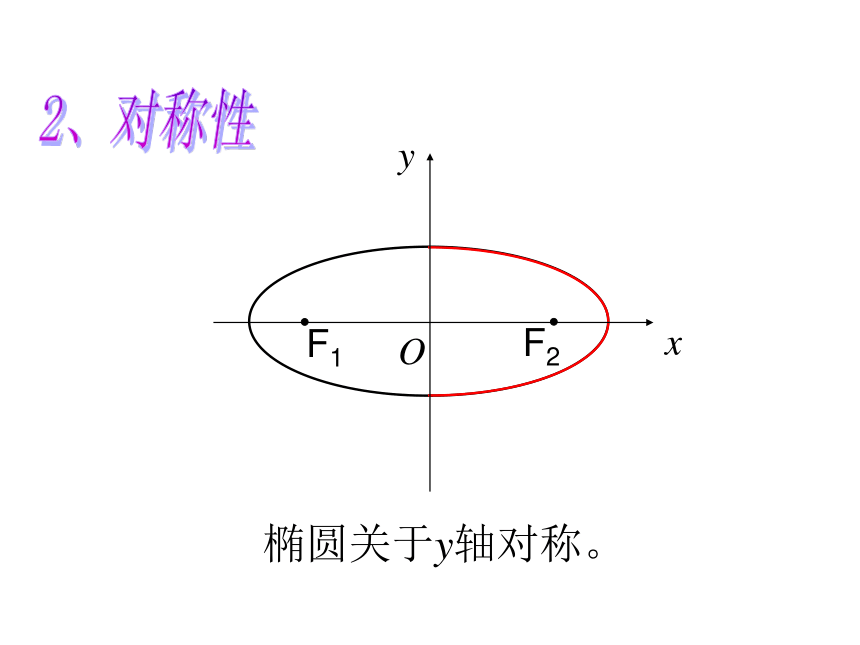
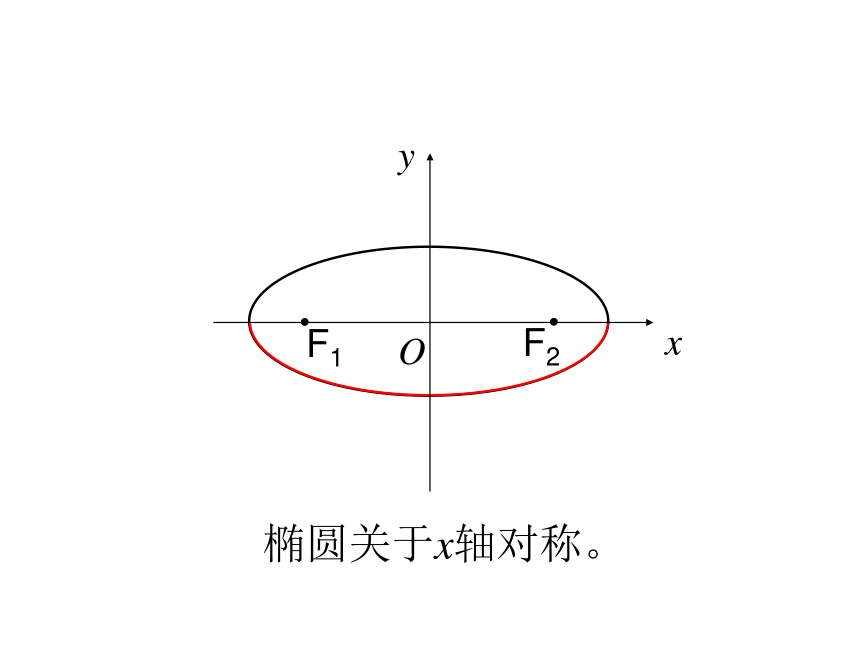
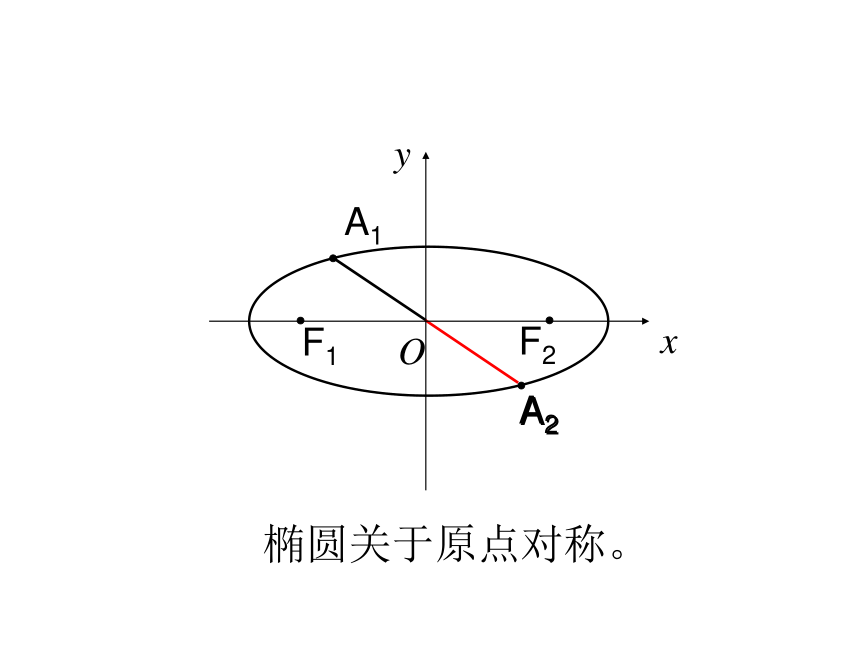
课件20张PPT。2.1.2椭圆的简单几何性质(一)复习:1.椭圆的定义:到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2当焦点在X轴上时当焦点在Y轴上时aF2F1OB2B1A1A2xycb容易算得:B2F2=a △B2F2O叫椭圆的特征三角形。1.范 围:2、对称性F2F1Oxy椭圆关于y轴对称。F2F1Oxy椭圆关于x轴对称。A2A1F2F1Oxy椭圆关于原点对称。从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
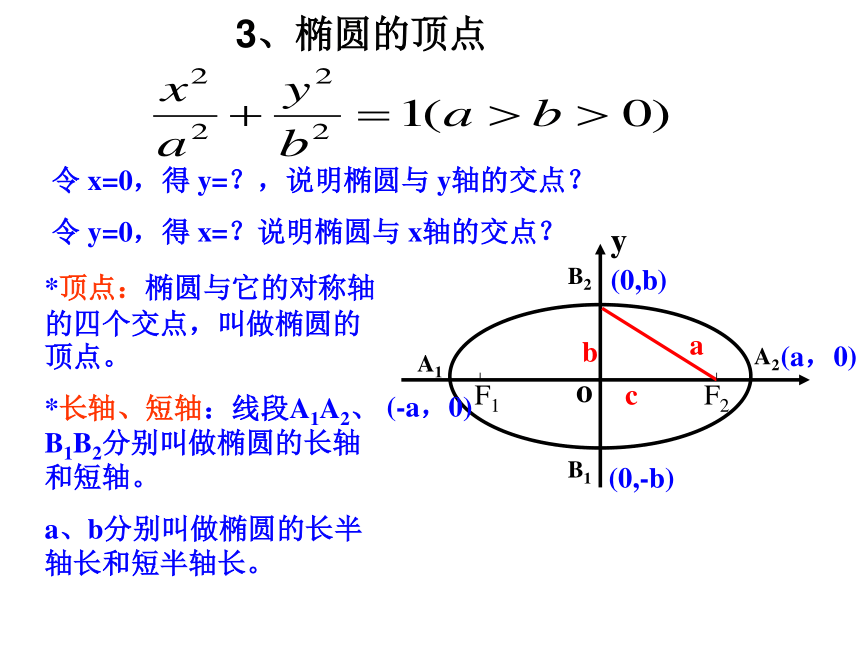
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。3、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。学生活动思考:已知椭圆的长轴A1A2和短轴B1B2 ,怎样确定椭圆焦点的位置? oB2B1A1A2F1F2因为a2=b2+c2,所以以椭圆短轴端点为圆心,a长为半径的圆与x轴的交点即为椭圆焦点.4、离心率上面椭圆的形状有什么变化?Oxy怎样刻画它们的扁平程度?扁的程度不同4、离心率Oxy如图,a不变,也即,a不变,把椭圆的焦距与长轴长的比 称为椭圆的离心率,用e表示,即b越小,椭圆越扁。c越大,椭圆越扁。4、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:[2]离心率对椭圆形状的影响:02)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆[3]e与a,b的关系:关于x轴、y轴成轴对称;关于原点成中心对称。长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标因此,椭圆的长轴长和短轴长分别是离心率焦点坐标分别是四个顶点坐标是解题的关键:1、将椭圆方程转化为标准方程
2、确定焦点的位置和长轴的位置顶点坐标为
(-5,0),(5,0),
(0,4),(0,-4)所以,长轴长2a=10,短轴长2b=8 ;离心率为0.6 ;焦点坐标为(-3,0),(3,0)已知椭圆方程为6x2+y2=6它的长轴长是: 。短轴长是:______________。
焦距是: .离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 2练习1.例2.过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .例3.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。答案:分类讨论的数学思想小结:本节课我们学习了椭圆的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义。了解了研究椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系,这对我们解决椭圆中的相关问题有很大的帮助,给我们以后学习圆锥曲线其他的两种曲线扎实了基础。在解析几何的学习中,我们更多的是从方程的形式这个角度来挖掘题目中的隐含条件,需要我们认识并熟练掌握数与形的联系。在本节课中,我们运用了几何性质,待定系数法来求解椭圆方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。3、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。学生活动思考:已知椭圆的长轴A1A2和短轴B1B2 ,怎样确定椭圆焦点的位置? oB2B1A1A2F1F2因为a2=b2+c2,所以以椭圆短轴端点为圆心,a长为半径的圆与x轴的交点即为椭圆焦点.4、离心率上面椭圆的形状有什么变化?Oxy怎样刻画它们的扁平程度?扁的程度不同4、离心率Oxy如图,a不变,也即,a不变,把椭圆的焦距与长轴长的比 称为椭圆的离心率,用e表示,即b越小,椭圆越扁。c越大,椭圆越扁。4、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:[2]离心率对椭圆形状的影响:0
2、确定焦点的位置和长轴的位置顶点坐标为
(-5,0),(5,0),
(0,4),(0,-4)所以,长轴长2a=10,短轴长2b=8 ;离心率为0.6 ;焦点坐标为(-3,0),(3,0)已知椭圆方程为6x2+y2=6它的长轴长是: 。短轴长是:______________。
焦距是: .离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 2练习1.例2.过适合下列条件的椭圆的标准方程:
(1)经过点 、 ;
(2)长轴长等于 ,离心率等于 .
解:(1)由题意, ,又∵长轴在
轴上,所以,椭圆的标准方程为 .
(2)由已知, ,
∴ , ,∴ ,
所以椭圆的标准方程为 或 .例3.已知椭圆的中心在原点,焦点在坐标轴上,长轴是短轴的三倍,且椭圆经过点P(3,0),求椭圆的方程。答案:分类讨论的数学思想小结:本节课我们学习了椭圆的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义。了解了研究椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系,这对我们解决椭圆中的相关问题有很大的帮助,给我们以后学习圆锥曲线其他的两种曲线扎实了基础。在解析几何的学习中,我们更多的是从方程的形式这个角度来挖掘题目中的隐含条件,需要我们认识并熟练掌握数与形的联系。在本节课中,我们运用了几何性质,待定系数法来求解椭圆方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想。
