平行线的性质
图片预览






文档简介
课件19张PPT。5.3 平行线的性质 利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行. 反过来,如果两条直线
平行,同位角、内错角、同旁内角各有什么关系呢? 试验 1:已知窗户的横格是平行的,用三角尺进行检验,发现同位角相等. 这个结论是否具有一般性呢?答:具有一般性. 试验 2:任意画一条直线 c 与平行线线 a, b 相交,选一对同位角来度量,这对同位角是否相等?
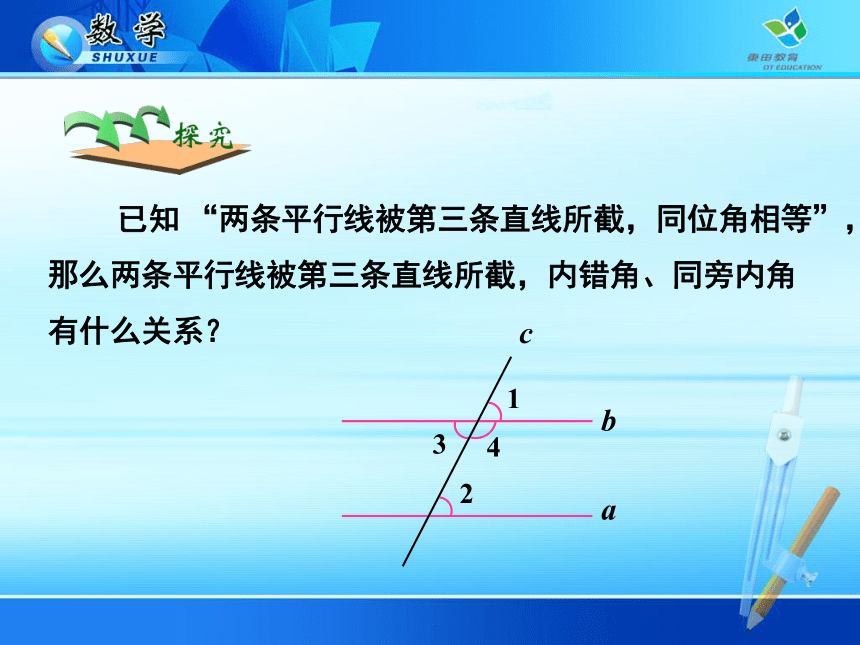
结论:两条平行直线被第三条直线所截,同位角相等. 已知 “两条平行线被第三条直线所截,同位角相等”,那么两条平行线被第三条直线所截,内错角、同旁内角
有什么关系? 解: (1) 内错角之间的数量关系. 如图,已知 a∥b,求证 : ∠2 =∠3.
证明:∵ a∥b,
∴ ∠1 =∠2.
又 ∠1 =∠3,
∴ ∠2 =∠3. (2) 同旁内角之间的数量关系. 如图,已知 a∥b,求证 : ∠2 +∠4 = 180o.
证明:∵ a∥b,
∴ ∠1 =∠2.
∵ ∠1 +∠4 = 180o,
∴ ∠2 +∠4 = 180o.
即两直线平行、内错角相等;两直线平行、同旁内角互补. 观察下列语句,你能发现它们有什么共同的特征吗?
(1) 两条平行线被第三条直线所截,同位角相等;
(2) 两条平行线被第三条直线所截,内错角相等;
(3) 对顶角相等;
(4) 如果两个角相等,那么这两个角的补角也相等. 命题:判断一件事情的语句叫做命题.
一个命题通常可以写成 “如果 ······ 那么 ······”的形式,“如果”后面的是题设(条件),“那么”后面的是结论. 1. 下图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A = 115o,∠D = 100o. 请你求出另外两个角的度数 (梯形的两底互相平行) .解: 因为 ABCD 是梯形,
所以 AD∥BC.
所以 ∠A +∠B = 180o,
∠D +∠C = 180o.
又 ∠A = 115o,∠D = 100o,
所以 ∠B = 65o,∠C = 80o. 2. 如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行. 第一次拐的 ∠B 等
于 142o,第二次拐的角 ∠C 是多少度?为什么? 解: 因为拐弯前后的两条路互相平行,所以容易得到∠B 和∠C 相等. 于是得到∠C = 142o. 3. 如图,一束平行光线 AB 与 DE 射向一个水平镜面后被反射,此时∠1 =∠2,∠3 =∠4.
(1)∠1, ∠3 的大小有什么关系?∠2 与∠4 呢?
(2) 反射光线 BC 与 EF 也平行吗?BE解:∵ AB 与 DE 是平行的,
∴ ∠1 =∠3.
又∵ ∠1 =∠2,∠3 =∠4,
∴ ∠2 =∠4.
∴ BC∥EF.BE 4. 如图,若 AB∥CD,你能确定∠B, ∠D 与∠BED的大小关系吗?解: 过点 E 作 EF∥AB,
∴ ∠B =∠BEF.
∵ AB∥CD,
∴ EF∥CD.
∴ ∠D =∠DEF.
∴ ∠B +∠D =∠BEF +∠DEF =∠BED.
即 ∠B +∠D =∠BED. 5. 下列语句是命题吗?若是,说出题设和结论;若不是,简单说明理由.
(1) 画线段 AB = CD;
(2) 今天下雨吗?
答: (1)(2) 不是命题,因为它们没有对任何事情作出判断. (3) 等式两边乘以同一个数,结果仍是等式;
(4) 如果两个角互补,那么它们是邻补角.
答:(3)(4) 是命题.
(3)的题设是 “等式两边乘以同一个数”,结论是 “结果仍是等式”;
(4)的题设是“两个角互补”,结论是“它们是邻补角”.1. 平行线的三个性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
2. 平行线的性质与平行线的判定有什么区别?
判定:已知角的关系得平行的关系. 证平行,用判定.
性质:已知平行的关系得角的关系. 知平行,用性质.
平行,同位角、内错角、同旁内角各有什么关系呢? 试验 1:已知窗户的横格是平行的,用三角尺进行检验,发现同位角相等. 这个结论是否具有一般性呢?答:具有一般性. 试验 2:任意画一条直线 c 与平行线线 a, b 相交,选一对同位角来度量,这对同位角是否相等?
结论:两条平行直线被第三条直线所截,同位角相等. 已知 “两条平行线被第三条直线所截,同位角相等”,那么两条平行线被第三条直线所截,内错角、同旁内角
有什么关系? 解: (1) 内错角之间的数量关系. 如图,已知 a∥b,求证 : ∠2 =∠3.
证明:∵ a∥b,
∴ ∠1 =∠2.
又 ∠1 =∠3,
∴ ∠2 =∠3. (2) 同旁内角之间的数量关系. 如图,已知 a∥b,求证 : ∠2 +∠4 = 180o.
证明:∵ a∥b,
∴ ∠1 =∠2.
∵ ∠1 +∠4 = 180o,
∴ ∠2 +∠4 = 180o.
即两直线平行、内错角相等;两直线平行、同旁内角互补. 观察下列语句,你能发现它们有什么共同的特征吗?
(1) 两条平行线被第三条直线所截,同位角相等;
(2) 两条平行线被第三条直线所截,内错角相等;
(3) 对顶角相等;
(4) 如果两个角相等,那么这两个角的补角也相等. 命题:判断一件事情的语句叫做命题.
一个命题通常可以写成 “如果 ······ 那么 ······”的形式,“如果”后面的是题设(条件),“那么”后面的是结论. 1. 下图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A = 115o,∠D = 100o. 请你求出另外两个角的度数 (梯形的两底互相平行) .解: 因为 ABCD 是梯形,
所以 AD∥BC.
所以 ∠A +∠B = 180o,
∠D +∠C = 180o.
又 ∠A = 115o,∠D = 100o,
所以 ∠B = 65o,∠C = 80o. 2. 如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行. 第一次拐的 ∠B 等
于 142o,第二次拐的角 ∠C 是多少度?为什么? 解: 因为拐弯前后的两条路互相平行,所以容易得到∠B 和∠C 相等. 于是得到∠C = 142o. 3. 如图,一束平行光线 AB 与 DE 射向一个水平镜面后被反射,此时∠1 =∠2,∠3 =∠4.
(1)∠1, ∠3 的大小有什么关系?∠2 与∠4 呢?
(2) 反射光线 BC 与 EF 也平行吗?BE解:∵ AB 与 DE 是平行的,
∴ ∠1 =∠3.
又∵ ∠1 =∠2,∠3 =∠4,
∴ ∠2 =∠4.
∴ BC∥EF.BE 4. 如图,若 AB∥CD,你能确定∠B, ∠D 与∠BED的大小关系吗?解: 过点 E 作 EF∥AB,
∴ ∠B =∠BEF.
∵ AB∥CD,
∴ EF∥CD.
∴ ∠D =∠DEF.
∴ ∠B +∠D =∠BEF +∠DEF =∠BED.
即 ∠B +∠D =∠BED. 5. 下列语句是命题吗?若是,说出题设和结论;若不是,简单说明理由.
(1) 画线段 AB = CD;
(2) 今天下雨吗?
答: (1)(2) 不是命题,因为它们没有对任何事情作出判断. (3) 等式两边乘以同一个数,结果仍是等式;
(4) 如果两个角互补,那么它们是邻补角.
答:(3)(4) 是命题.
(3)的题设是 “等式两边乘以同一个数”,结论是 “结果仍是等式”;
(4)的题设是“两个角互补”,结论是“它们是邻补角”.1. 平行线的三个性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
2. 平行线的性质与平行线的判定有什么区别?
判定:已知角的关系得平行的关系. 证平行,用判定.
性质:已知平行的关系得角的关系. 知平行,用性质.
