平移（新人教）

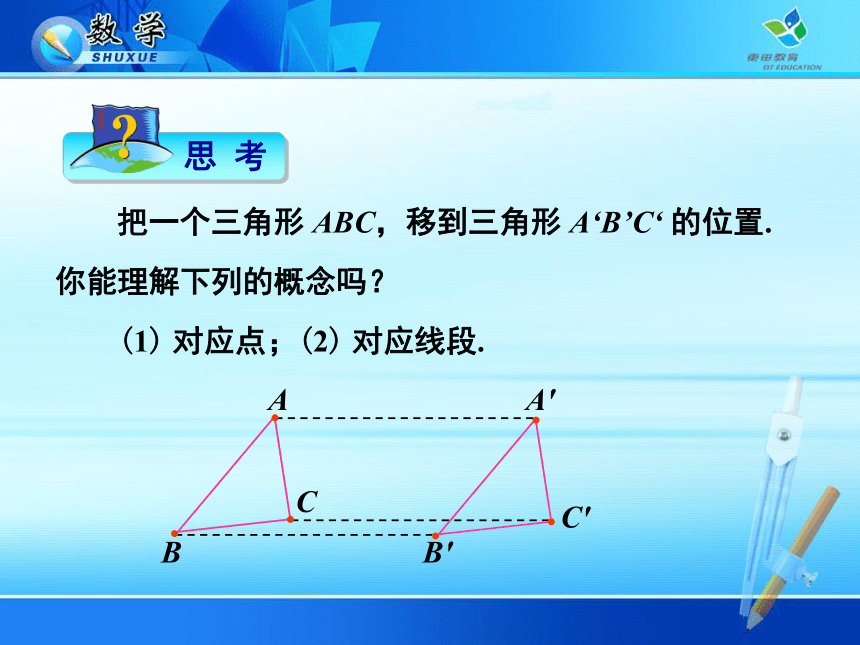
课件14张PPT。5.4 平 移 平移：图形的平行移动就是平移. 把一个三角形 ABC，移到三角形 A‘B’C‘ 的位置. 你能理解下列的概念吗？
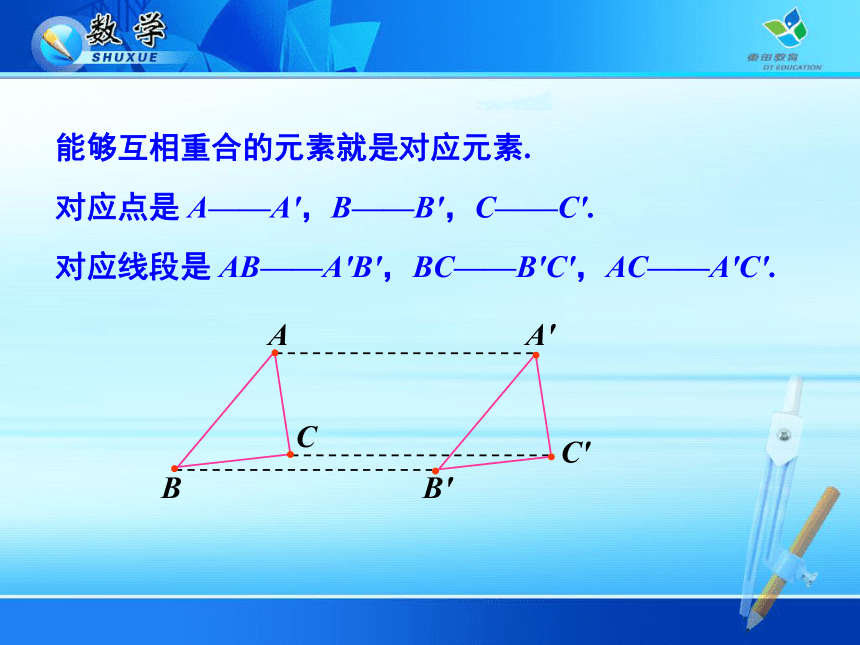
(1) 对应点；(2) 对应线段.能够互相重合的元素就是对应元素.
对应点是 A——A'，B——B'，C——C'.
对应线段是 AB——A'B'，BC——B'C'，AC——A'C'. 在所画出的相邻两个雪人中，找出三组对应点(例如，它们的鼻尖 A 与 A’，帽顶 B 与 B’，纽扣 C 与 C’)，连接这些对应点，观察
得出的线段，它们的位
置、长短有什么关系? 可以发现, AA’∥BB’∥CC’，且 AA’ = BB’ = CC’.
即把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同.
新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点. 连接各组对应点的线段平行且相等. 平移的性质：
1. 对应线段平行且相等(平移是图形的平行移动)；
2. 对应点所连线段平行且相等(都是平移的距离). 如图，平移三角形 ABC，使点 A 移动到点 A’，画出平移后的三角形 A’B’C’.
分析: 图形平移后的对应点有什么特征？再作出点
B 和点 C 的对应点 B’, C’，
能确定△A’B’C’ 吗？ 解: 如图，连接 AA’，过点 B 作 AA’ 的平行线 l，
在 l 上截取 BB’ = AA’，则点 B’ 就是点 B 的对应点.
类似地，你能作出点 C 的对应点 C’，并进一步得出
平移后的三角形 A’B’C’ 吗？动手试一试.lA’ABCB’ 1. 如图， △ABC 经过平移到达△A’B’C’ 的位置，
(1)请指出平移的距离和方向；
(2)点 D, E, F 经过平移
到了什么位置？ 解: (1) 平移的方向是 A——A’ 的方向，距离是 AA’的长度.
(2) 如下图. 2. 如图，将△ABC 先下移 2 个格再右移 4 个格得到△A'B'C'. 作出平移后的图形.1. 平移特征:
(1)图形形状、大小不变；
(2)连接对应点的连线平行且相等；
2. 利用平移的性质作图.