1.2.2.2 分段函数与映射 同步训练(含答案)
文档属性
| 名称 | 1.2.2.2 分段函数与映射 同步训练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 102.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-12 00:00:00 | ||
图片预览


文档简介
1.2.2.2 分段函数与映射 同步训练(含答案)
一、选择题
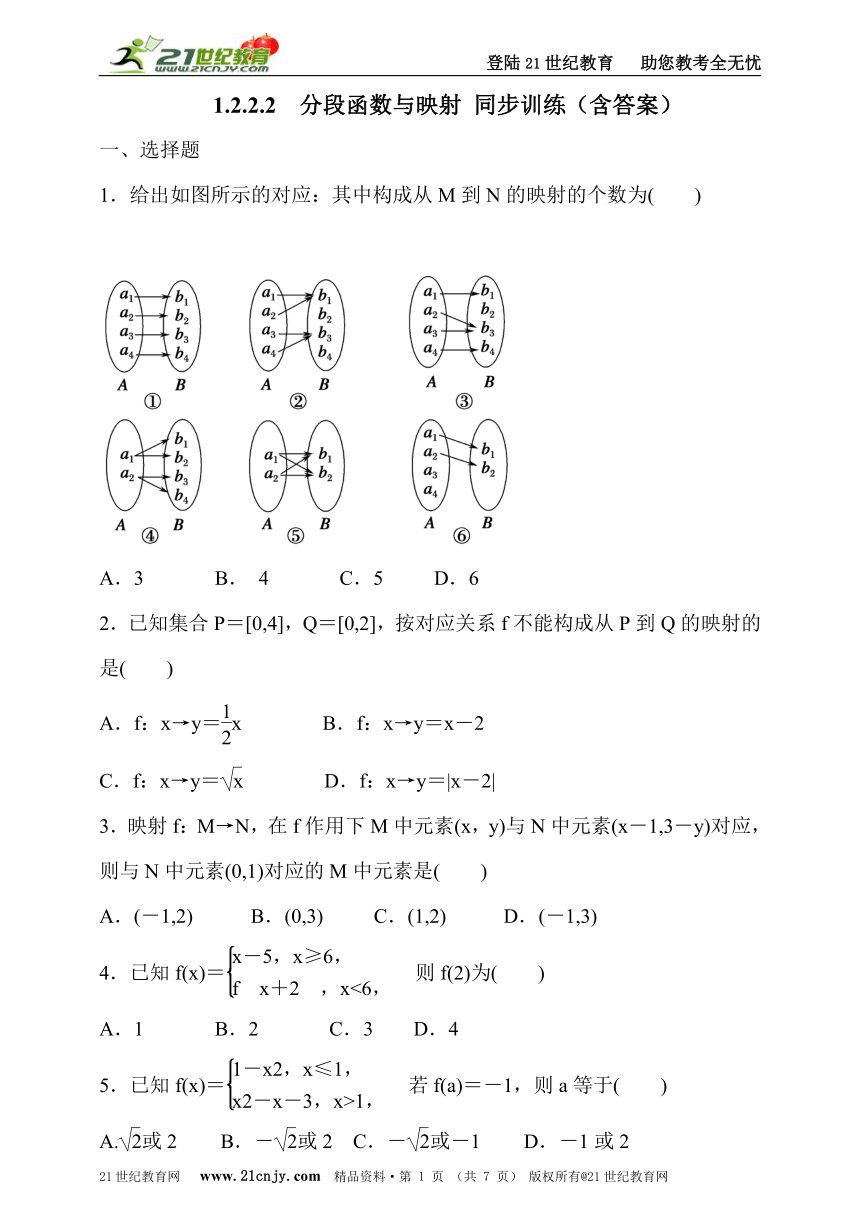
1.给出如图所示的对应:其中构成从M到N的映射的个数为( )
A.3 B. 4 C.5 D.6
2.已知集合P=[0,4],Q=[0,2],按对应关系f不能构成从P到Q的映射的是( )
A.f:x→y=x B.f:x→y=x-2
C.f:x→y= D.f:x→y=|x-2|
3.映射f:M→N,在f作用下M中元素(x,y)与N中元素(x-1,3-y)对应,则与N中元素(0,1)对应的M中元素是( )21教育网
A.(-1,2) B.(0,3) C.(1,2) D.(-1,3)
4.已知f(x)=则f(2)为( )
A.1 B.2 C.3 D.4
5.已知f(x)=若f(a)=-1,则a等于( )
A.或2 B.-或2 C.-或-1 D.-1或2
6.拟定从A地到B地通话m分钟的话费符合f(m)=其中[m]表示不超过m的最大整数,从A地到B地通话5.3分钟的话费是( )【来源:21·世纪·教育·网】
A.3.71 B.4.24 C.4.77 D.7.95
7.设函数f(x)=.若f(f())=4,则b=( )
A.1 B. C. D.
设函数f(x)=若f(-4)=f(0),f(-2)=-2,则关于x的方程f(x)-x=0的解的个数是( ).21·cn·jy·com
A.1 B.2 C.3 D.4
二、填空题
9.已知函数f(x)=若f(f(0))=5a,则实数a=________.
10.若A={2,4,6,8},B={-1,-3,-5,-7},下列对应关系①f:x→7-2x;②f:x→1-x;③f:x→7-x;④f:x→x-9中,能确定A到B的映射的是________.www.21-cn-jy.com
11.设函数f(x)=,若f(f(a))=2,则a=________.
12.设定义在R上的函数f(x)满足f(x+1)=2f(x).若当0≤x≤1时,f(x)=x(1-x),则当-1≤x≤0时,f(x)=________.21·世纪*教育网
13.在校大学生提前创业,想开一家服装专卖店,经过预算,店面装修费为10 000元,每天需要房租水电等费用100元,受营销方法、经营信誉度等因素的影响,专卖店销售总收入P与店面经营天数x的关系是P(x)=则总利润最大时店面经营天数是________.
三、解答题
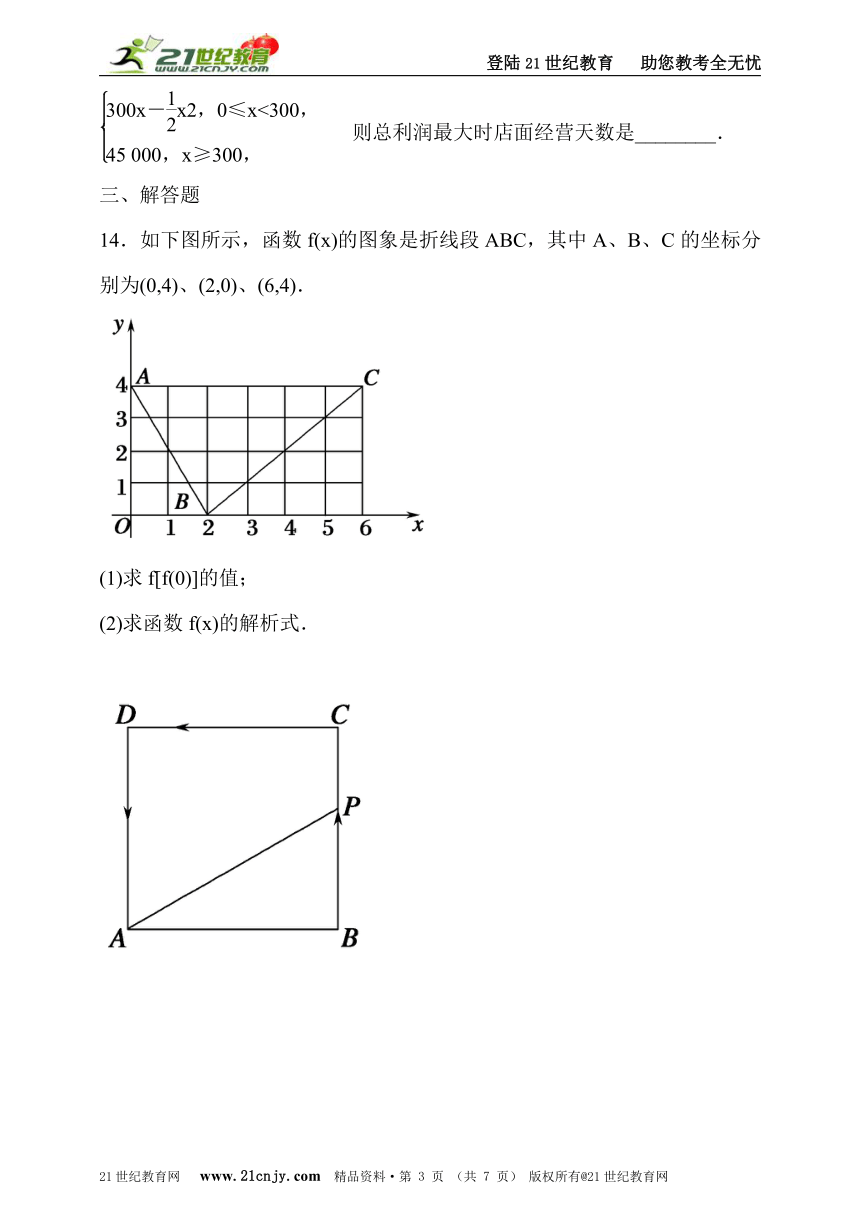
14.如下图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).www-2-1-cnjy-com
(1)求f[f(0)]的值;
(2)求函数f(x)的解析式.
15.如上图所示,在边长为4的正方形ABCD上有一点P,沿着折线BCDA由B点(起点)向A点(终点)移动.设P点移动的路程为x,△ABP的面积为y=f(x).2-1-c-n-j-y
(1)求△ABP的面积与P移动的路程的函数关系式;
(2)作出函数的图象,并根据图象求f(x)的最大值.
参考答案:
1.解析:①是映射,是一对一;②③是映射,满足对于集合M中的任意一个元素在集合N中都有唯一的元素和它对应;④⑤不是映射,是一对多;⑥不是映射,a3、a4在集合N中没有元素与之对应.答案:A21cnjy.com
2.答案:B
3.解析:由题意知解得所以与N中元素(0,1)对应的M中元素是(1,2).答案:C
4.解析:f(2)=f(2+2)=f(4),f(4)=f(4+2)=f(6).∵f(6)=6-5=1,故f(2)=1.答案:A2·1·c·n·j·y
5.解析:当a≤1时,由f(a)=-1得1-a2=-1,解得a=±,又a≤1,所以a=-.当a>1时,由f(a)=-1得a2-a-3=-1,即a2-a-2=0,解得a=-1或a=2.又因为a>1,所以a=2.综上,a=-或2.故选B.
答案:B
6.解析:f(5.3)=1.06×(0.5×[5.3]+2)=1.06×(2.5+2)=4.77.答案:C
7.解析:f(f())=f(3×-b)=f(-b)当-b<1,即b>时,3×(-b)-b=4,解得b=(舍).当-b≥1,即b≤时,2×(-b)=4,
解得b=.故选D.答案:D
8.解析:由f(-4)=f(0)?(-4)2+b×(-4)+c=c,f(-2)=-2?(-2)2+b×(-2)+c=-2,解得b=4,c=2.则f(x)= 由f(x)-x=0,得x2+4x+2=x?x2+3x+2=0?x=-2或x=-1,即当x≤0时,有两个解.当x>0时,有一个解x=2.综上,f(x)-x=0有3个解.故选C
答案:C
9.解析:由题意知f(0)=2.又f(2)=22+2a,所以22+2a=5a,即a=.
答案:
10.解析:对于①,在A中取2时,在B中没有元素与之对应,故①不是映射;②④满足映射的定义,是映射;对于③,在A中取2,4,6时,在集合B中均没有元素与之对应,故③不是映射.答案:②④21世纪教育网版权所有
11.解析:当a≤0时,f(a)=a2+2a+2>0,f(f(a))<0,显然不成立;当a>0时,f(a)=-a2,f(f(a))=a4-2a2+2=5,则a=±,故a=.答案:
12.解析:当-1≤x≤0时,0≤x+1≤1,所以f(x+1)=(x+1)[1-(x+1)]=-x(x+1),又f(x+1)=2f(x),以f(x)=f(x+1)=-.
答案:-
13.解析:设总利润为L(x),则L(x)=
当0≤x<300时,L(x)max=10 000,当x≥300时,L(x)max=5 000,
所以总利润最大时店面经营天数是200.答案:200
14.解:(1)直接由图中观察,可得f[f(0)]=f(4)=2.
(2)设线段AB所对应的函数解析式为y=kx+b,将与代入,得∴∴y=-2x+4(0≤x≤2).同理,线段BC所对应的函数解析式为y=x-2(215.解:(1)函数的定义域为(0,12).当0(2)图象如图所示.从图象可以看出[f(x)]max=8.
一、选择题
1.给出如图所示的对应:其中构成从M到N的映射的个数为( )
A.3 B. 4 C.5 D.6
2.已知集合P=[0,4],Q=[0,2],按对应关系f不能构成从P到Q的映射的是( )
A.f:x→y=x B.f:x→y=x-2
C.f:x→y= D.f:x→y=|x-2|
3.映射f:M→N,在f作用下M中元素(x,y)与N中元素(x-1,3-y)对应,则与N中元素(0,1)对应的M中元素是( )21教育网
A.(-1,2) B.(0,3) C.(1,2) D.(-1,3)
4.已知f(x)=则f(2)为( )
A.1 B.2 C.3 D.4
5.已知f(x)=若f(a)=-1,则a等于( )
A.或2 B.-或2 C.-或-1 D.-1或2
6.拟定从A地到B地通话m分钟的话费符合f(m)=其中[m]表示不超过m的最大整数,从A地到B地通话5.3分钟的话费是( )【来源:21·世纪·教育·网】
A.3.71 B.4.24 C.4.77 D.7.95
7.设函数f(x)=.若f(f())=4,则b=( )
A.1 B. C. D.
设函数f(x)=若f(-4)=f(0),f(-2)=-2,则关于x的方程f(x)-x=0的解的个数是( ).21·cn·jy·com
A.1 B.2 C.3 D.4
二、填空题
9.已知函数f(x)=若f(f(0))=5a,则实数a=________.
10.若A={2,4,6,8},B={-1,-3,-5,-7},下列对应关系①f:x→7-2x;②f:x→1-x;③f:x→7-x;④f:x→x-9中,能确定A到B的映射的是________.www.21-cn-jy.com
11.设函数f(x)=,若f(f(a))=2,则a=________.
12.设定义在R上的函数f(x)满足f(x+1)=2f(x).若当0≤x≤1时,f(x)=x(1-x),则当-1≤x≤0时,f(x)=________.21·世纪*教育网
13.在校大学生提前创业,想开一家服装专卖店,经过预算,店面装修费为10 000元,每天需要房租水电等费用100元,受营销方法、经营信誉度等因素的影响,专卖店销售总收入P与店面经营天数x的关系是P(x)=则总利润最大时店面经营天数是________.
三、解答题
14.如下图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).www-2-1-cnjy-com
(1)求f[f(0)]的值;
(2)求函数f(x)的解析式.
15.如上图所示,在边长为4的正方形ABCD上有一点P,沿着折线BCDA由B点(起点)向A点(终点)移动.设P点移动的路程为x,△ABP的面积为y=f(x).2-1-c-n-j-y
(1)求△ABP的面积与P移动的路程的函数关系式;
(2)作出函数的图象,并根据图象求f(x)的最大值.
参考答案:
1.解析:①是映射,是一对一;②③是映射,满足对于集合M中的任意一个元素在集合N中都有唯一的元素和它对应;④⑤不是映射,是一对多;⑥不是映射,a3、a4在集合N中没有元素与之对应.答案:A21cnjy.com
2.答案:B
3.解析:由题意知解得所以与N中元素(0,1)对应的M中元素是(1,2).答案:C
4.解析:f(2)=f(2+2)=f(4),f(4)=f(4+2)=f(6).∵f(6)=6-5=1,故f(2)=1.答案:A2·1·c·n·j·y
5.解析:当a≤1时,由f(a)=-1得1-a2=-1,解得a=±,又a≤1,所以a=-.当a>1时,由f(a)=-1得a2-a-3=-1,即a2-a-2=0,解得a=-1或a=2.又因为a>1,所以a=2.综上,a=-或2.故选B.
答案:B
6.解析:f(5.3)=1.06×(0.5×[5.3]+2)=1.06×(2.5+2)=4.77.答案:C
7.解析:f(f())=f(3×-b)=f(-b)当-b<1,即b>时,3×(-b)-b=4,解得b=(舍).当-b≥1,即b≤时,2×(-b)=4,
解得b=.故选D.答案:D
8.解析:由f(-4)=f(0)?(-4)2+b×(-4)+c=c,f(-2)=-2?(-2)2+b×(-2)+c=-2,解得b=4,c=2.则f(x)= 由f(x)-x=0,得x2+4x+2=x?x2+3x+2=0?x=-2或x=-1,即当x≤0时,有两个解.当x>0时,有一个解x=2.综上,f(x)-x=0有3个解.故选C
答案:C
9.解析:由题意知f(0)=2.又f(2)=22+2a,所以22+2a=5a,即a=.
答案:
10.解析:对于①,在A中取2时,在B中没有元素与之对应,故①不是映射;②④满足映射的定义,是映射;对于③,在A中取2,4,6时,在集合B中均没有元素与之对应,故③不是映射.答案:②④21世纪教育网版权所有
11.解析:当a≤0时,f(a)=a2+2a+2>0,f(f(a))<0,显然不成立;当a>0时,f(a)=-a2,f(f(a))=a4-2a2+2=5,则a=±,故a=.答案:
12.解析:当-1≤x≤0时,0≤x+1≤1,所以f(x+1)=(x+1)[1-(x+1)]=-x(x+1),又f(x+1)=2f(x),以f(x)=f(x+1)=-.
答案:-
13.解析:设总利润为L(x),则L(x)=
当0≤x<300时,L(x)max=10 000,当x≥300时,L(x)max=5 000,
所以总利润最大时店面经营天数是200.答案:200
14.解:(1)直接由图中观察,可得f[f(0)]=f(4)=2.
(2)设线段AB所对应的函数解析式为y=kx+b,将与代入,得∴∴y=-2x+4(0≤x≤2).同理,线段BC所对应的函数解析式为y=x-2(2
