广东省华侨中学2017届高三上学期摸底考试数学(理)试题
文档属性
| 名称 | 广东省华侨中学2017届高三上学期摸底考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 222.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-12 00:00:00 | ||
图片预览



文档简介
普宁华侨中学2017届高三摸底考试
高三理科数学
2016
09
05
第I卷(选择题共60分)
一、选择题(本大题12小题,每小题5分,共60分)
1.若集合则a的取值范围是(
)
A.
B.
C.
D.
2.复数(是虚数单位)等于(
)
A.
B.
C.
D.
3.命题“若,则”的否命题是(
)
A.若,则
B.若,则
C.若,则
D.若,则
4.已知动点P(x,y)满足,则点P的轨迹是(
)
A.两条相交直线
B.抛物线
C.双曲线
D.椭圆
5.函数
(a>0,且a≠1)的图象恒过定点A,若点A在直线
上,其中m>0,n>0,则的最小值为(
)
A.
B.4
C.
D.
6.设椭圆C:(a>b>0)的左、右焦点分别为F1、F2,P是C上的点且PF2F1F2,∠PF1F2=30°,则C的离心率为()
A.
B.
C.
D.
7.在中,是的中点,,点在上且满足,则等于
A.
B.
C.
D.
8.
已知sin-3cos=0,则()。
A.
B.
C.2
D.
9.已知数列{an}是等差数列,a1+a
( http: / / www.21cnjy.com )3+a5=105,a2+a4+a6=99,{an}的前n项和为Sn,则使得Sn达到最大的n是(
)
A.18
B.19
C.20
D.21
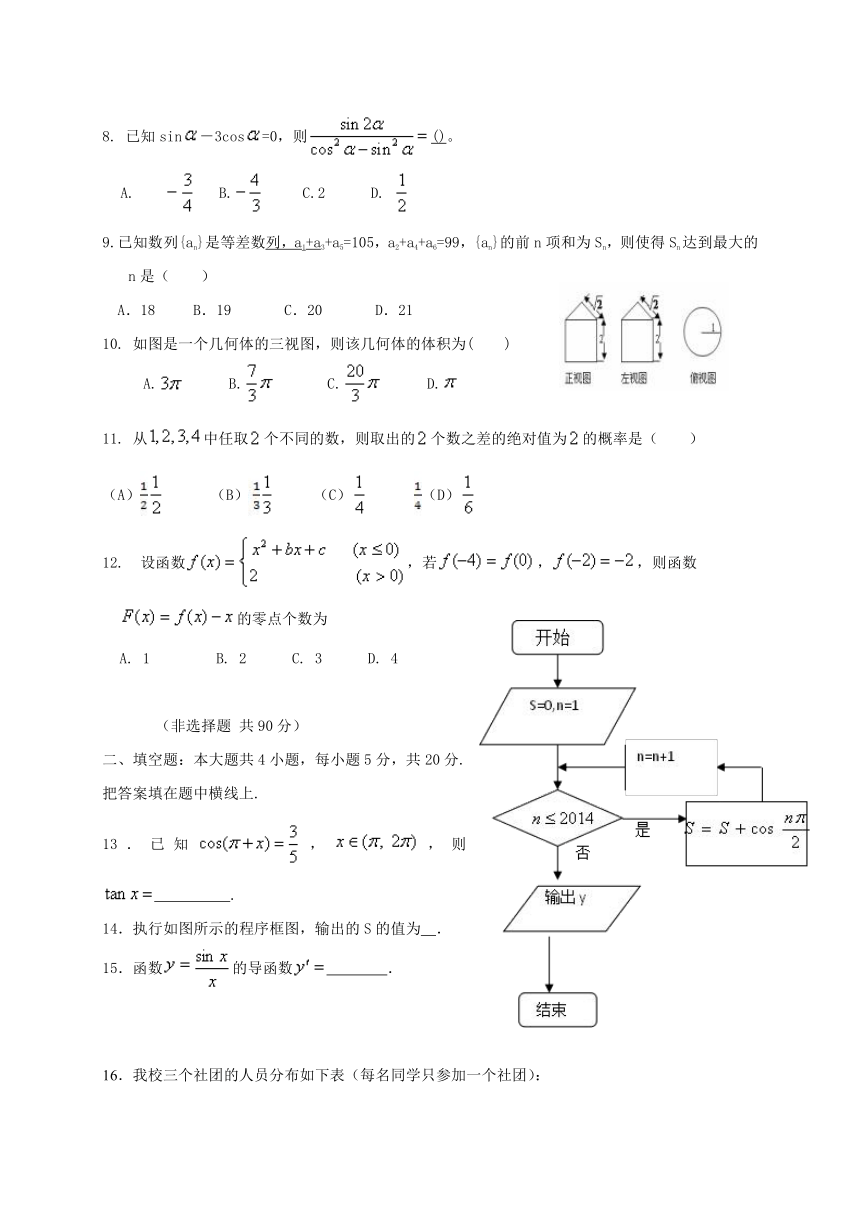
10.
如图是一个几何体的三视图,则该几何体的体积为(
)
A.
B.
C.
D.
11.
从中任取个不同的数,则取出的个数之差的绝对值为的概率是(
)
(A)
(B)
(C)
(D)
12.
设函数,若,,则函数的零点个数为
A.
1
B.
2
C.
3
D.
4
(非选择题
共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.已知,,则
.
14.执行如图所示的程序框图,输出的S的值为
.
15.函数的导函数
.
我校三个社团的人员分布如下表(每名同学只参加一个社团):
心晴社
话剧社
羽毛球社
高一
45
30
高二
15
10
20
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取人,结果心晴被抽出人,则的值为
.
三、解答题:本大题共6小题,共60分.解答应写出文字说明、证明过程或演算步骤。
17.
(本小题满分12分)在△ABC中,角A、B、C的对边分别是a、b、c,且c
=
2,C
=.
(1)若△ABC的面积等于,求a、b;
(2)若
sin
C
+
sin(B
-
A)
=
sin
2
A,求A的值.
18.(本小题满分12分)某公司计划购买2
( http: / / www.21cnjy.com )台机器,该种机器使用三年后即被淘汰,机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元,在机器使用期间,如果备件不足再购买,则每个500元。现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了
100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替
( http: / / www.21cnjy.com )1台机器更换的
易损零件数发生的概率,记X表示2台机器三年内共需更换的
易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)
≥0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
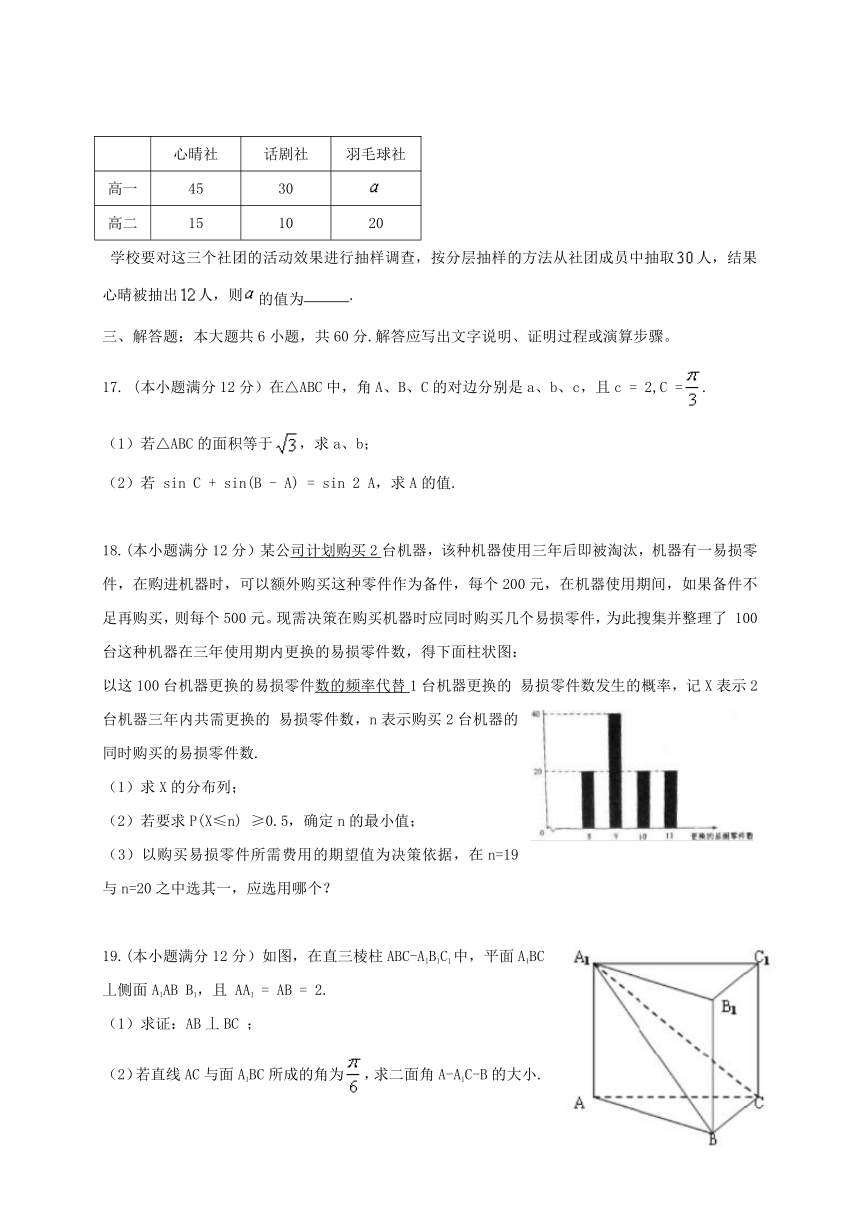
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB
B1,且
AA1
=
AB
=
2.
(1)求证:AB丄BC
;
(2)若直线AC与面A1BC所成的角为,求二面角A-A1C-B的大小.
20.
(本小题满分12分)已知椭圆
(a
>
b
>
0)的一个焦点是F
(1,0),O为坐标原点.
(1)已椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(2)设过点F的直线L交椭圆于A,B两点,若直线L绕点F任意转动,恒有|OA|2
+
|OB|2
<|AB|2,求a的取值范围.
21.(本小题满分12分)已知函数
(1)求函数的单调区间和极值;
(2)已知函数与函数的图像关于直线x
=
1对称,证明:当x>1时,f(x)
>
g(x);
(3)如果,证明:.
四.选做题(从22,
23,
24三道题中选一题作答)
22.(本小题满分10分)选修:几何证明选做题
如图所示,直线PA为圆O的切线,切点为A,直径BC丄OP,连结AB交PO于点D.
(1)证明:PA
=
PD
;
(2)证明:PA
AC
=
AD
OC
.
23.(本小题满分10分)选修:极坐标与参数方程
在直角坐标系中,直线L的参数方程
(t为参数),在O为极点,x轴非负半轴为为极轴的极坐标系中,曲线C的极坐标方程为.
(1)求直线L的普通方程与曲线C的直角坐标方程;
(2)若直线L与y轴的交点为P,直线L与曲线C的交点为A,B,求|PA||PB|的值.
24.(本小题满分10分)选修:不等式选讲
设函数,其中a∈R.
(1)当a
=
2时,解不等式
;
(2)若对于任意实数,恒有成立,求a的取值范围。
高三(理科)数学答案
一选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的
1
2
3
4
5
6
7
8
9
10
11
12
A
D
C
A
D
A
A
A
B
B
B
C
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
13.
14.
-1
15.
16.
30
解答题
17.(1)c=3,C=,由余弦定理得,
故联立上面两式,解得
…6分
(2),即;
.则分类讨论若;若,
则,由正弦定理b=2a,又,故
,即.综上…12分
18.
解:(1)由柱状图并以频率代替概率可得,一台机器在三年内需更换的易损零件数为8,9,10,
11的概率分别为0.2,0.4,0.2,0.2,从而;
;
;
;
;
;
.
所以的分布列为
16
17
18
19
20
21
22
…4分
(2)由(Ⅰ)知,,故的最小值为19.
…8分
(3)记表示2台机器在购买易损零件上所需的费用(单位:元).
当时,
当时,
.
可知当时所需费用的期望值小于时所需费用的期望值,故应选.…12分
19.(1)取A1B的中点为D,连接AD
(2)角ACD即AC与面A1BC所成线面角,等于;直角三角形ABC中A1A=AB=2,
D为AB的中点,
过A作,且.
故即为二面角的一个平面角.
又,
,且二面角是锐二面角,
…12分
解法二:以BC,BA,BB1分别为x,y,z轴建系,故分别求得面A1BC的法向量为(0,1,-1)
,
面A1AC的法向量为(1,1,0),求得法向量夹角余弦…12分
20.(1)设M,N为短轴的两个三等分点,由△MNF
为正三角形,
即1=,
椭圆的方程为.
…4分
(2)AB与x轴重合,则…5分
AB与x轴不重合,令AB方程为,联立,即
,且,…7分
恒有,故为钝角,即恒成立,…9分
整理得
对于恒成立,此时的最小值为0.
又,,
解得
…12分
21.(1)在上增,在上减,故在x=1处
取得极大值
…4分
(2)因为函数的图像与的图像关于直线x=1对称,所以
=,令,则
又,当时有,
在上为增函数,∴.
…8分
(3)
在上增,在上减,且,
∴x1,
x2分别在直线x=1两侧,不妨设x1<1,x2>1,
∴即,∵∴
又
∴∴.
…12分
22.(1)直线PA为圆O的切线,切点为A,,BC为圆O的直径,
∴∵
∴
…5分
(2)连接,由(1)得
∵,∴
∴
∴
…10分
23.(1)∵直线的参数方程为,∴,∴直线的普通方程为,又∵,∴曲线的直角坐标方程为;
…5分
(2)将直线的参数方程(为参数)代入曲线:,得到:,,.…
10分
24.
(Ⅰ)时,就是
当时,,得,不成立;
当时,,得,所以;
当时,,即,恒成立,所以.
综上可知,不等式的解集是.
…5分
(Ⅱ)
因为,
所以的最大值为.
对于任意实数,恒有成立等价于.
当时,,得;
当时,,,不成立.
综上,所求的取值范围是
.…10分
高三理科数学
2016
09
05
第I卷(选择题共60分)
一、选择题(本大题12小题,每小题5分,共60分)
1.若集合则a的取值范围是(
)
A.
B.
C.
D.
2.复数(是虚数单位)等于(
)
A.
B.
C.
D.
3.命题“若,则”的否命题是(
)
A.若,则
B.若,则
C.若,则
D.若,则
4.已知动点P(x,y)满足,则点P的轨迹是(
)
A.两条相交直线
B.抛物线
C.双曲线
D.椭圆
5.函数
(a>0,且a≠1)的图象恒过定点A,若点A在直线
上,其中m>0,n>0,则的最小值为(
)
A.
B.4
C.
D.
6.设椭圆C:(a>b>0)的左、右焦点分别为F1、F2,P是C上的点且PF2F1F2,∠PF1F2=30°,则C的离心率为()
A.
B.
C.
D.
7.在中,是的中点,,点在上且满足,则等于
A.
B.
C.
D.
8.
已知sin-3cos=0,则()。
A.
B.
C.2
D.
9.已知数列{an}是等差数列,a1+a
( http: / / www.21cnjy.com )3+a5=105,a2+a4+a6=99,{an}的前n项和为Sn,则使得Sn达到最大的n是(
)
A.18
B.19
C.20
D.21
10.
如图是一个几何体的三视图,则该几何体的体积为(
)
A.
B.
C.
D.
11.
从中任取个不同的数,则取出的个数之差的绝对值为的概率是(
)
(A)
(B)
(C)
(D)
12.
设函数,若,,则函数的零点个数为
A.
1
B.
2
C.
3
D.
4
(非选择题
共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.已知,,则
.
14.执行如图所示的程序框图,输出的S的值为
.
15.函数的导函数
.
我校三个社团的人员分布如下表(每名同学只参加一个社团):
心晴社
话剧社
羽毛球社
高一
45
30
高二
15
10
20
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取人,结果心晴被抽出人,则的值为
.
三、解答题:本大题共6小题,共60分.解答应写出文字说明、证明过程或演算步骤。
17.
(本小题满分12分)在△ABC中,角A、B、C的对边分别是a、b、c,且c
=
2,C
=.
(1)若△ABC的面积等于,求a、b;
(2)若
sin
C
+
sin(B
-
A)
=
sin
2
A,求A的值.
18.(本小题满分12分)某公司计划购买2
( http: / / www.21cnjy.com )台机器,该种机器使用三年后即被淘汰,机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元,在机器使用期间,如果备件不足再购买,则每个500元。现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了
100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替
( http: / / www.21cnjy.com )1台机器更换的
易损零件数发生的概率,记X表示2台机器三年内共需更换的
易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)
≥0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB
B1,且
AA1
=
AB
=
2.
(1)求证:AB丄BC
;
(2)若直线AC与面A1BC所成的角为,求二面角A-A1C-B的大小.
20.
(本小题满分12分)已知椭圆
(a
>
b
>
0)的一个焦点是F
(1,0),O为坐标原点.
(1)已椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(2)设过点F的直线L交椭圆于A,B两点,若直线L绕点F任意转动,恒有|OA|2
+
|OB|2
<|AB|2,求a的取值范围.
21.(本小题满分12分)已知函数
(1)求函数的单调区间和极值;
(2)已知函数与函数的图像关于直线x
=
1对称,证明:当x>1时,f(x)
>
g(x);
(3)如果,证明:.
四.选做题(从22,
23,
24三道题中选一题作答)
22.(本小题满分10分)选修:几何证明选做题
如图所示,直线PA为圆O的切线,切点为A,直径BC丄OP,连结AB交PO于点D.
(1)证明:PA
=
PD
;
(2)证明:PA
AC
=
AD
OC
.
23.(本小题满分10分)选修:极坐标与参数方程
在直角坐标系中,直线L的参数方程
(t为参数),在O为极点,x轴非负半轴为为极轴的极坐标系中,曲线C的极坐标方程为.
(1)求直线L的普通方程与曲线C的直角坐标方程;
(2)若直线L与y轴的交点为P,直线L与曲线C的交点为A,B,求|PA||PB|的值.
24.(本小题满分10分)选修:不等式选讲
设函数,其中a∈R.
(1)当a
=
2时,解不等式
;
(2)若对于任意实数,恒有成立,求a的取值范围。
高三(理科)数学答案
一选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的
1
2
3
4
5
6
7
8
9
10
11
12
A
D
C
A
D
A
A
A
B
B
B
C
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
13.
14.
-1
15.
16.
30
解答题
17.(1)c=3,C=,由余弦定理得,
故联立上面两式,解得
…6分
(2),即;
.则分类讨论若;若,
则,由正弦定理b=2a,又,故
,即.综上…12分
18.
解:(1)由柱状图并以频率代替概率可得,一台机器在三年内需更换的易损零件数为8,9,10,
11的概率分别为0.2,0.4,0.2,0.2,从而;
;
;
;
;
;
.
所以的分布列为
16
17
18
19
20
21
22
…4分
(2)由(Ⅰ)知,,故的最小值为19.
…8分
(3)记表示2台机器在购买易损零件上所需的费用(单位:元).
当时,
当时,
.
可知当时所需费用的期望值小于时所需费用的期望值,故应选.…12分
19.(1)取A1B的中点为D,连接AD
(2)角ACD即AC与面A1BC所成线面角,等于;直角三角形ABC中A1A=AB=2,
D为AB的中点,
过A作,且.
故即为二面角的一个平面角.
又,
,且二面角是锐二面角,
…12分
解法二:以BC,BA,BB1分别为x,y,z轴建系,故分别求得面A1BC的法向量为(0,1,-1)
,
面A1AC的法向量为(1,1,0),求得法向量夹角余弦…12分
20.(1)设M,N为短轴的两个三等分点,由△MNF
为正三角形,
即1=,
椭圆的方程为.
…4分
(2)AB与x轴重合,则…5分
AB与x轴不重合,令AB方程为,联立,即
,且,…7分
恒有,故为钝角,即恒成立,…9分
整理得
对于恒成立,此时的最小值为0.
又,,
解得
…12分
21.(1)在上增,在上减,故在x=1处
取得极大值
…4分
(2)因为函数的图像与的图像关于直线x=1对称,所以
=,令,则
又,当时有,
在上为增函数,∴.
…8分
(3)
在上增,在上减,且,
∴x1,
x2分别在直线x=1两侧,不妨设x1<1,x2>1,
∴即,∵∴
又
∴∴.
…12分
22.(1)直线PA为圆O的切线,切点为A,,BC为圆O的直径,
∴∵
∴
…5分
(2)连接,由(1)得
∵,∴
∴
∴
…10分
23.(1)∵直线的参数方程为,∴,∴直线的普通方程为,又∵,∴曲线的直角坐标方程为;
…5分
(2)将直线的参数方程(为参数)代入曲线:,得到:,,.…
10分
24.
(Ⅰ)时,就是
当时,,得,不成立;
当时,,得,所以;
当时,,即,恒成立,所以.
综上可知,不等式的解集是.
…5分
(Ⅱ)
因为,
所以的最大值为.
对于任意实数,恒有成立等价于.
当时,,得;
当时,,,不成立.
综上,所求的取值范围是
.…10分
同课章节目录
